Loeng 5. Jõuväljad
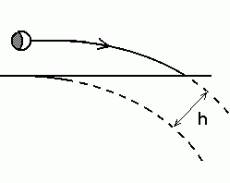
Tõsi on see, et juba 22 aastat enne "Printsiipide" ilmumist, aastal 1665 avaldas Newton (oli siis kõigest 22 aastat vana!) arvamust, et planeetide liikumist juhivad raskusjõuga sama tüüpi jõud. Planeetide kohta käivad Kepleri seadused avaldati aastal 1619, kehade vaba langemise seaduse (kõik kehad langevad ühesuguse kiir(end)usega sõltumatult nende kaalust) avastas umbes samal ajal Galilei. Legend Newtonist, taevas paistvast Kuust ja kukkuvast õunast on hästi tuntud ja üsna tõepärane. Niisiis:
|
Ülemaailmse gravitatsiooniseaduse formuleeris Isaac Newton 1665. aastal.
|
|
Paraku arvati 1665.a., et Kuu kaugus Maast on 200000 km. Valem ei klappinud ja Newtonil tuli oodata 20 aastat, enne kui astronoomid oma vea parandasid.
Jääb üle leida veel võrdetegur. Et astronoomidel oli "valemi
häälestamiseks" terve Päikesesüsteem, saadi selle leidmisega ruttu
hakkama. Juba Newton teadis, et kordajaks on
6.67 Räägime sellest nii pikalt selle pärast, et gravitatsiooniseaduse avastamine (sõnastamine?) on tegelikult Newtoni füüsika sõlmpunkt. Nii gravitatsiooniseadus kui Newtoni II seadus (inertsiseadus) seovad vastasmõju parameetri - jõu - kehade sisemise parameetri -massiga. Mõlemas valemis jõud on võrdelises sõltuvuses massist: |
Maapealsete kehade korral on gravitatsioonijõud kaduvväike ja tema mõõtmine nõuab ülitäpset eksperimenti.
|
|
Miks need massid (inertne ja gravitatsiooniline) võrdsed on, selle
kohta Newton "hüpoteese ei püstita". Ka tunnistas ta, et sellist
seost pole võimalik tuletada ühestki teisest füüsika seadusest.
Masside võrdsust on
korduvalt kontrollitud, üheteistkümne numbrikoha ulatuses on nad
samad. Vaba langemise seaduse formuleeris A. Einstein 1916.a. nn
ekvivalentsusprintsiibina:
Ekvivalentsusprintsiibil rajaneb
tänapäeva valitsev
gravitatsiooniteooria - üldrelatiivsusteooria. Selle järgi
pole inertsiaalne (ühtlane sirgjooneline) liikumine põhimõtteliselt
eristatav kõverjoonelisest (kiirendusega) liikumisest
gravitatsiooniväljas. Einstein formuleeris selle samaväärsuse
ruumi kõverdumisena massiivsete kehade lähedal. Keerulise
matemaatikaga teooria on sisemiselt kooskõlaline, igapäevaelus
vajadus tema kasutamiseks puudub - Newtoni teooria on siin piisavalt
täpne ja märksa kergemini rakendatav.
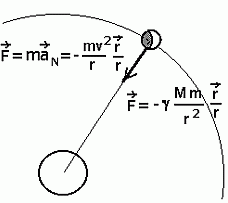
Kuna liikumise uurimine eeldab nagunii taustkeha olemasolu, võime lugeda selleks välja tekitava keha, nii, et taustkeha ja välja allikas moodustavad liikumise kirjeldamiseks vaja mineva taustsüsteemi - näiteks on ortonormaalne reeper, kus välja allikas asub koordinaadistiku nullpunktis. Teljed võime suunata suvaliselt.
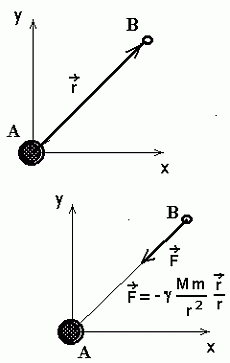
Liikuv keha, mille asukoha määrab kohavektor |
|
|
Valemist on näha, et igale liikuvale kehale mõjuv jõud sõltub selle keha massist. Seda liikumisvõrrandi seisukohalt ebamugavat asjaolu saab kergesti kõrvaldada, defineerides välja iseloomustava suuruse - väljatugevuse:
|
|
|
Liikumisvõrrrandit teha on veel lihtsam: kuna keha kiirenduse leidmiseks tuleb leitud jõud (uuesti) massiga jagada, siis
|
Väljatugevuseks antud punktis nimetatakse seal asuvale ühikulise massiga kehale mõjuvat jõudu. |
|
Saime väga mugava valemi. Koordinaatides väljendatuna: Kui välja tekitavad mitu (punkt)allikat, tuleb väljatugevused summeerida. Seda võime teha nii vektorite kui koordinaatide tasemel. Mida aga teha siis, kui allikas polegi punktallikas? Siis läheb integreerimiseks, aga sellest täpsemalt elektri-osas. |
Liikumisvõrrandi koostamiseks on otstarbekas ühendada teiste kehade mõjud ning avaldada saadud jõud kohavektori (ruumikoordinaatide) funktsioonina
|
|
Gravitatsiooniväljas on punktmass välja allikaks. Füüsikas pole see ei esimene ega ainuke punktallikas. Valgusõpetuse - optika - fotomeetria-osas defineeritakse punktallikas, mille poolt esile kutsutud valgustatus kahaneb (pöörd)võrdeliselt kauguse ruuduga. Sama seaduse kohaselt kahaneb ka elektri- ja magnetväljade tugevus. Jääb mulje, et kõigil neil juhtudel on tegemist teatud ruumipunktist kiirguva mõjuvooga, mis ruumi hajudes jaotub üha laiemale pinnale. Et allikat ümbritseva sfääri pindala on võrdeline raadiuse (tsentri kauguse) ruuduga, jaguneb tsentrist lähtuv (energia, mõju)voog kaugusega võrdelisele pindalale. Kui lugeda mõju mõõduks pinnaühiku kohta tulev voog, saamegi mõju kahanemise pöördvõrdeliselt kauguse ruuduga - pöördruutsõltuvuse (ingl. inverse square relation). |
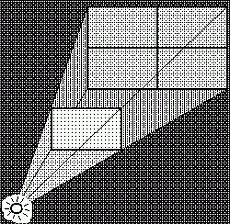
et lambist kiirguv valgus jaotub järjest suuremale pinnale, kahaneb pinna valgustatus (pöörd)võrdeliselt kauguse ruuduga - niisamuti kahaneb ka gravitatsioonijõud. |
|
Väidetavalt kajastub pöördruutsõltuvustes reaalse ruumi kolmemõõtmelisus. Valguse nõrgenemise seletusena on see omal kohal, miks aga kehtib (ja kas alati kehtib?) sama seadus jõuväljade korral, pole nii endastmõistetav. Kaasaegne jõuväljade kvant-teooria tuletab pöördruutsõltuvuse sootuks teistsugustest printsiipidest. Praktilise rakenduse seisukohalt on tegemist matemaatiliselt äärmiselt ebamugava diferentsiaalvõrrandiga 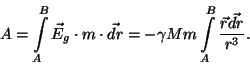
Kuidas sellest võrrandist aru saada? Integraali aluse avaldise lugejas on vektorite skalaarkorrutis
Kuidas tsiteeritud korrutis tekib? |
|
|
Kumb kummale, on matemaatiliselt ükspuha. Matemaatiliselt on
Nüüd läheb kiiresti. Integraal skalaarkorrutisest muutub lihtsaks ühemõõtmeliseks (määratud) integraaliks piki raadiust: 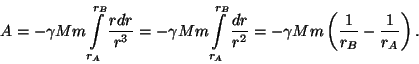
|
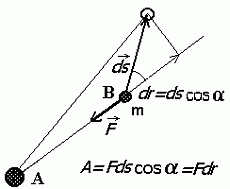
Gravitatsioonijõu töö ei sõltu liikumisteest. |
|
Mida see meile ütleb? Kõigepealt seda, et
Ja loomulikult tuleb arvestada märgireeglit: Siingi on matemaatiline väljapääs: tuleb kokku leppida, et potentsiaalne energia vähemalt pöördruutsõltuvusega väljades on negatiivne. Ainult sel teel saab vastuolu lahendada. Meenutame, et tegelikult on määratud vaid potentsiaalse energia muut. Kui tahame saada valemisse kindlaid arve, tuleb energia väärtus mingil kaugusel ette anda. Praegu me normeerisime energia nulliks lõpmata kaugel allikast. Seegi määrang kõlbab - ja on, nagu järgnevalt näeme, äärmiselt otstarbekas. |
|
|
Tekkinud väli - nimetame teda potentsiaaliväljaks - kuulub tevenisti allika juurde. Vaadates mingi teise keha liikumist, saame leida selle poolt tehtava töö, korrutades potentsiaali muudu vaadeldava keha massiga.
|
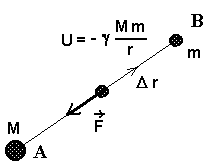
Punktmassi potentsiaal. Mida kaugemale viia keha B, seda rohkem tuleb teha tööd ja seda suurem on potentsiaalne energia. |
|
Võtame gravitatsioonivälja potentsiaali avaldisest tuletise Et asi ei jääks liiga lihtsaks, tuletame meelde, et erinevalt potentsiaalist on väljatugevus vektor, st. teda iseloomustab kindel suund. Meie näites on küll juba teada, et jõud mõjub koordinaadistiku alguspunkti (välja allika) suunas. Üldjuhul ei tarvitse see nii olla. Näiteks kui meil on kaks välja allikat ja need mõlemad mõjutavad vaadeldavat keha. |
|
|
Püüame tabada probleemi sisemist loogikat. Väljatugevus on
potentsiaali tuletis tee pikkuse (täpsemalt nihke) järgi. Ta on
vektor, järelikult peab tal olema suund. Kui keha liigub selles
suunas, on temale mõjuv jõud samasuunaline nihkega. Sellisel juhul
peab potentsiaal muutuma kõige kiiremini, kuna töö valemisse kuuluv
liige
Kasutame diferentsiaalarvutust. Potentsiaali muutus (ühikulise massi
nihutamisel tehtud töö) on lõpmata väikesel nihkel
Teeme veel ühe matemaatilise nipi. Potentsiaal |
|
|
ehk, kasutades vektoranalüüsi sümboolikat.
|
Välja kui ruumifunktsiooni tuletist koordinaatide järgi nimetataks gradiendiks.
Jõuvälja valemi leidmiseks on tihti lihtsam leida potentsiaalivälja valem ja võtta sellest tuletis (gradient).
|
|
Aga aitab selleks korraks.
|
|
|
Teades, et potentsiaali tuletiseks on väljatugevus, võime väita, et kehale mõjuv jõud on potentsiaalse energia tuletiseks. Niisiis: kuna tasakaaluolekus peab kehale (süsteemile) mõjuv jõud olema null, on nulliga võrdne potentsiaalse energia tuletis. Kõrgemast matemaatikast on teada, et funktsiooni tuletis on null seal, kus funktsioon omab ekstremaalset (maksimaalset või minimaalset) väärtust. Seega on süsteem tasakaalus parajasti siis, kui tema potentsiaalne energia omab maksimaalset või minimaalset väärtust. |
Süsteemi tasakaaluasend on tuletatav potentsiaalse energia miinimumi lausest. |
|
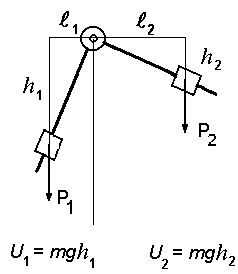
Pöörlevat süsteemi uurides leidsime, et tal oli kaks tasakaaluasendit, üks neist (alumine) oli püsiv, teisest (ülemisest) läks süsteem välja juba väikese häirituse tagajärjel. Proovime seda hinnata potentsiaalse energia tuletiste abil. Võtame potentsiaalsest energiast teist järku tuletise - see on jõu (esimene tuletis!) tuletis nihke järgi Kui see tuletis on negatiivne, kutsub nihe esile jõu, mis on suunatud nihkele vastassuunas. Sellist jõudu nimetatakse taastavaks jõuks ja ta püüab süsteemi tasakaaluasendisse tagasi viia. Sellist tasakaalu nimetatakse püsivaks tasakaaluks. Kui teine tuletis on positiivne, tekib nihkega samasuunaline jõud ja tasakaal kaob. |
|
|
Mida öeldakse teist järku tuletiste kohta? Matemaatilises analüüsis tähendab negatiivne teist järku tuletis funktsiooni maksimumi, positiivne miinimumi. Meie seade peaks selle loogika järgi püüdlema maksimaalse potentsiaalse energiaga asendi (ülemise "surnud punkti") poole. Millest niisugune absurdne järeldus? Mõelge. Annan vihje: vaadake märgiprobleemi! Seniks aga potentsiaalse energia miinimumi lause:
See on loodusseadus: kõik mehaanilised, füüsikalised, keemilised jne. süsteemid püüdlevad minimaalse energiaga seisundi poole. Mehaanilised süsteemid on neist kõige lihtsamad, edaspidises tutvume ka keerulisemate süsteemide dünaamikaga. Lõpetuseks ülesanne: näidake, et ka meie teise masina tasakaaluseisund on tuletatav potentsiaalse energia miinimumi lausest! |
|
 10 -11Nm2kg-2.
Muidugi oli tolleaegsete ühikute järgi ka
konstandil teine väärtus. Et tegu on äärmiselt väikese arvuga (kaks
tonnist tinamuna tõmbavad teineteist meetri kauguselt jõuga
6.65
10 -11Nm2kg-2.
Muidugi oli tolleaegsete ühikute järgi ka
konstandil teine väärtus. Et tegu on äärmiselt väikese arvuga (kaks
tonnist tinamuna tõmbavad teineteist meetri kauguselt jõuga
6.65