Loeng 2. Paigalseis ja liikumine

  Sisukorda

Staatika Tasakaalu tingimused Tasakaal pöörlemisel Tasakaal kulgliikumisel Kinemaatika Aeg Ruum ja koordinaadid Aja ja ruumi ühikud Liikumisvõrrand Pöörlemise võrrand Liikumisvõrrandi diferentseerimine

Staatika Sõnaga "staatika" (kr. statos -- tasakaal) tähistatakse füüsikas tasakaaluõpetust. Tasakaaluseisundid on matemaatiliselt lihtsamalt kirjeldatavad, kuna ajaline sõltuvus (muutumine) puudub. Seepärast kasutatakse staatika valemeid ka keerulisemates süsteemides (näiteks automootoris) toimuvate protsesside uurimisel, kujutades neid protsesse tasakaaluseisundite ajalise järgnevusena. Staatika jaguneb alaliikideks vastavalt uuritavale objektile. Nii kirjeldab hüdrostaatika (kr. hydor -- vesi) vedelike tasakaalu, elektrostaatika elektriliselt laetud kehade tasakaalu jne. Kui lisandit pole, mõeldakse tavaliselt tahkete makrokehade tasakaaluseisundi uurimist.	Staatika uurib olukorda, kus keha (süsteemi) olek ei muutu.
Tasakaalu tingimused. Staatika on lihtne ka sellepärast, et ta koosneb ühest ainsast seadusest: Keha on tasakaalus parajasti siis, kui: a) temale mõjuvate jõudude summa on null; b) temale mõjuvate jõumomentide summa on null.
Alustame keeleõppest. Jõud on suurus, mille abil kirjeldatakse kehade vastasmõju. Keha on üldnimi kõiksugu asjade kohta juhul, kui nende eripära meid ei huvita (näiteks liikumise seisukohalt). Vastasmõju ei tähenda midagi enamat kui vastastikust ("sina mulle - mina sulle") mõjustamist. Füüsikas on vastasmõju tagajärjeks oleku muutus, ja oleku all mõistame keha kirjeldavate parameetrite väärtuste (täielikku) komplekti. "Täielikkku" on sulgudes sellepärast, et enamuse ülesannete korral ei muutu korraga kõik parameetrid - seega võime oleku muutuse uurimisel mittemuutuvad parameetrid vaatluse alt välja jätta.	Definitsioonid meelde jätta!
Mehaanikas tähendab oleku muutus liikumise muutust: paigalseisev keha hakkab liikuma, liikuv keha muudab oma kiirust või liikumissuunda. Liikumist ennast on kahte tüüpi: kulgev liikumine, kui vabalt liigutatav keha muudab oma asukohta ja pöörlev liikumine, kui keha on kinnitatud (pöörlemisteljele) ja võib seetõttu vaid pöörduda, muutes oma ruumilist orientatsiooni (asendit ruumis). Ehkki mõlemat tüüpi liikumised toimuvad samaaegselt, võib neid tavaliselt eraldi kirjeldada: auto liikumine maanteel loetakse kulgevaks ja sellest lähtuvalt ehitatakse välja nii tema kere ja vedrustus kui maantee profiil; samal ajal töötab kogu jõuseade ning ülekanded pöörlevas liikumises, mistõttu nende konstrueerimisel võib kulgliikumise seadused arvestamata jätta.	Asukoht:         toas         laual         tänaval Kulgev liikumine on asukoha muutus Asend:         püsti         külili         kummuli Pöörlev liikumine on asendi muutus
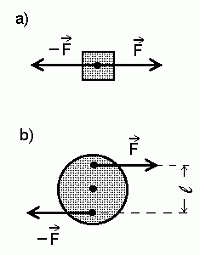
Tasakaalus keha ei tohi hakata ei "kulgema" ega pöörlema. Ülaltoodud seaduse kaks tingimust käivadki kahe liikumise tüübi kohta. Tasakaal pöörlemise suhtes. Kui kehale mõjuvate jõudude summa on null, ei saa ta muuta oma kulgliikumist. Aga ta võib hakata pöörlema - juhul, kui kaks vastassuunalist jõudu moodustavad jõupaari, st. mõjuvad keha erinevatesse punktidesse nii, et tekib pöörlemine. Sellise mõjustuse mõõtmiseks kasutatakse mõistet "jõumoment" - suurust, mis kirjeldab pöölemise muutuse põhjuseks olevat vastasmõju liiki. Arvutamise seisukohalt on oluline, et jõumomendi määrab lisaks jõu suurusele ka see, kui kaugel pöörlemisteljest ta keha mõjutab. Jõumomendiks $M=F\cdot l$ nimetatakse jõu $F$  ja tema õla pikkuse  $l$  korrutist; jõu õlg on võrdne jõu mõjumissihi kaugusega pöörlemisteljest. Nüüd on selge ka tasakaalutingimuse teise poole mõte. Kui kaks jõudu mõjuvad kehale vastassuunas piki samat sirget, on summa igal juhul null. Aga summa on null ka siis, kui sirged on erinevad, kuid paralleelsed. Kuid sellised jõud on suutelised keha pöörama - kuni saab nulliks ka nende jõudude momentide summa.	NB! Paljud füüsikalised suurused - nagu siin jõumoment - defineeritakse algebralise seose (valemi) abil. Suunatud suuruse -- vektori -- märgi muutmine tähendab suuna muutumist vastupidiseks.
Õpikutes kasutatakse mõnikord väljendit "algebraline summa". Sellega tahetakse öelda, et ei piisa, kui jõudusid väljendavad numbrid tuimalt kokku liita. Tuleb arvestada jõudude märke ja kontrollida, kas pole tegu vektoritega. Kui jõud mõjuvad piki sama sirget, piisab märkidest. Kui mitte, tuleb kasutada vektoreid. Jõumomendid - juhul, kui keha on teljele kinnitatud, võivad teda pöörata kas ühes või teises suunas; niisiis piisab ka siin märkidest. See, kumba pööret lugeda positiivseks ja kumba negatiivseks, on kokkuleppe asi, tavaliselt loetakse positiivseks pööre vastu kellaosuti liikumise suunda - nii, et pööre suurendaks pöördenurka. Staatikas, st. tasakaaluolukorras, pole sel loomulikult tähtsust, valida võib mõlemat pidi ja oluline on vaid see, et erisuunalised pöörded oleks ka erimärgilised. Staatika pole lihtne, ja eesseisvas teoreetilise mehaanika kursuses õpitakse seda põhjalikult. Meie piirdume kahe (lihtsa?) valemiga. Neist esimene (ühedimensionaalne) annab pöörlemistasakaalu valemi: $$M_{res}=\sum_i F_il_i\equiv F_1l_1+F_2l_2+\dots =0$$	a) jõudude tasakaal; b) jõupaar
Tasakaal kulgeva liikumise suhtes. Teine - vektorvalem (kahe- või kolmedimensionaalne) $$\sum_i \vec{F_i}\equiv \vec{F_1}+\vec{F_2}+\dots=0$$ paneb tasakaalu lõplikult paika. Kehtima peavad need kaks valemit loomulikult samaaegselt, muidu poleks ju tasakaalu.   Vaadelda (matemaatilist mudelit teha) võib aga eraldi. Pakun välja kaks "masinat", esimese pöörlemis-, teise kulgemistasakaalu jaoks: Ülemisel pildil on ratas, mida pööravad täisnurga all olevatele varrastele kinnitatud raskused. Ratas võib teljel pöörelda ning kui tal on tasakaaluasend, peab ülaltoodud tingimus olema täidetud. Arvutuse teeb raskemaks see, et lihtne on määrata koormise kaugust pöörlemisteljest, mitte aga jõu mõjumissihi kaugust, st. jõu õlga. Viimane sõltub seadeldise orientatsioonist (ratta pöördenurgast), mis muutub ratta pöördumise käigus. Alumisel pildil on mudel, kus proovikehale K mõjuvad koormiste P1 ,P2 ,P3 poolt tekitatud jõud F1 ,F2 ,F3. Kus on proovikeha tasakaaluasend? Mõlemal probleemil on geomeetriline lahend. Jõumomentide korral on selleks nn. Archimedese kangi valem: Kang on tasakaalus siis, kui tema õlgadele riputatud koormiste kaugus toetuspunktist on pöördvõrdeline koormise kaaluga. See tähendab, et kui joonisel on vasakpoolse koormise P1 mass kaks korda suurem kui P2 mass, pöörab seadeldis end nii, et kaugus koormisest P1 kuni pöörlemisteljest tõmmatud vertikaalini on kaks korda väiksem kui koormise P2 kaugus. Muidugi ei tohi nad olla samal pool seda vertikaali. Aga miks? Alumise "masina" lahend on samuti geomeetriline: et kolme vektori summa oleks null, peavad nad üksteise otsa tõstetuna moodustama suletud joone - hulknurga. Antud juhul siis kolmnurga. Kui sellise kolmnurga joonistamine on võimalik, on võimalik ka tasakaal. Aga kui ei ole? Ja millisel juhul ei ole? Veel üks probleem: Kolmest lõigust annab kokku panna ainult ühe kolmnurga, ja sedagi mitte alati. See-eest rohkema arvu jõudude korral on võimalike kinniste murdjoonte arv suurem. Näiteks võime neljast lõigust kokku panna juba kaks kinnist joont: Mida see tähendab tasakaalu koha pealt? Pingutage ajusid!   Kinemaatika "Kinemaatika" tuleneb kreekakeelsest sõnast kinema ehk lühemalt kino. Tähendab see liikumist; ja vastav mehaanika osa uuribki liikumist - mitte niivõrd selle põhjusi kui just liikumise matemaatilise kirjeldamise võimalusi.
Aeg. Liikumine tähendab asukoha ning asendi (orientatsiooni) muutumist. Muutumine, erinevalt püsivast seisundist (staatika!) nõuab vähemalt kaht parameetrit, millest üks on argumendiks (muutub sõltumatult liikuvast kehast), teine aga väljendab liikumist ennast. Kui argumenti pole täpsustatud (näiteks lausega "rõhu sõltuvus temperatuurist"), on sõltumatuks argumendiks aeg. Aja muutumine pole meie poolt kontrollitav, aeg muutub iseenesest (nagu tihti öeldakse - voolab) ja seetõttu kulgeb enamus looduslikke protsesse nagunii olekute ajalise järgnevusena. Seejuures pole aeg ise ühegi protsessi põhjustajaks. Aeg pole ka mõõdetav, vähemalt mitte nii, nagu me mõõdame tavalisi suurusi. See, mida me nimetame "aja mõõtmiseks" on tavaliselt mingi ajas kulgeva protsessi võrdlemine teise, lihtsama (perioodilise) protsessiga, nagu Maa pöörlemine või kellapendli võnkumine.	Aja mõiste sisse toomine annab võimaluse võrrelda erinevaid liikumisi. - ehk liikumisi võrreldakse aja mõiste abil. Kas saite aru? Mõelge hoolega!
Veel räägitakse, et aeg voolab ainult ühes suunas (minevikust tulevikku) ja seepärast on kõik põhjuslikku laadi seosed võimalikud vaid sel kujul, et põhjus eelneb (ajaliselt) tagajärjele. Mida selline aeg endast kujutab, selle üle on filosoofid vaielnud aastatuhandeid. Matemaatika vaatepunktist on aeg universaalne ja väga kasulik vahemuutuja, mille abil saab siduda üsnagi erinevate protsesside võrrandeid. Kogu see jutt ei tohiks häirida meie igapäevaseid suhteid ajaga. Kell on hea riist, pole tähtis, miks ja kuidas ta töötab. Peaasi, et aega näitab.	Aja nool: põhjus t1 peab eelnema tagajärjele t2,st t1< t2
Ruum ja koordinaadid. Niisiis on liikumine keha asukoha muutus, mis väljendub sel viisil, et mingil ajamomendil oli keha ühes, mingil teisel momendil aga teises kohas. Seda "kohta" saame määrata vaid teiste kehade suhtes; matemaatiliselt on asukohta kõige parem väljendada kohavektoriga $\vec r$, mis algab ühe ja lõpeb teise keha juures. Seda keha, kust vektor lähtub, nimetatakse taustkehaks ja nii peab kohavektori muutumine väljendama uuritava keha liikumist taustkeha suhtes.	Kohavektor on suunatud lõik taustkehast uuritava kehani. Ta näitab uuritava keha asukohta taustkeha suhtes
Füüsikud tavatsevad ütelda, et liikumine toimub kolmemõõtmelises eukleidilises ruumis. Matemaatiliselt on ruum mitmeparameetriliste muutujate hulk, millest igaüht kirjeldab korraga kaks või rohkem arvu. Tegelikult on ruumi mõiste tulnud matemaatikasse just füüsikast, kus ta tähistab "kohta, kus liiguvad kehad". Eestikeelne termin on tulnud saksa keelest (Raum - tuba), inglise keel kasutab siin mõistet "tühjus" (space), vene keel mõistet "ulatus" (prostranstvo ). Selle igapäevase ruumi matemaatiliseks kirjeldamiseks töötasid vanad kreeklased välja erilise teaduse - geomeetria, mis rajanes deduktiivsetel järeldustel Eukleidese poolt kirja pandud viiest aksioomist. Alles möödunud sajandil leidsid matemaatikud, et Eukleidese ruum polegi ainuvõimalik, vaid kujutab erijuhtu, üleminekuvormi kahe kõvera ruumi - avatud (hüperboolse) meetrikaga Lobatševski ruumi ning suletud (elliptilise) Riemanni ruumi vahel. Küll on aga Eukleidese ruum neist kõige lihtsam ja kuna ta on tavafüüsika tarbeks ka piisavalt täpne, kasutatakse teda endistviisi. Ainult väga tugevate jõuväljade ning ülisuurte mastaapide korral kasutatakse ka mitte-eukleidilisi ruume.	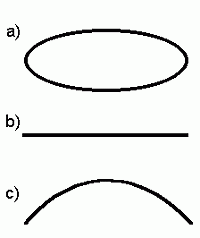Ühemõõtmelised ruumid: elliptiline; tasane; hüperboolne.
Koordinaadid. Termin kolmemõõtmeline väljendab vektori kirjapanekuks vajalike sõltumatute muutujate - koordinaatide - hulka. Igapäevakogemus kinnitab. et keha asukoha määramiseks piisab kolmest arvust (tinglikult pikkus, laius ja kõrgus). Nende kolme arvu saamiseks tuleb konstrueerida koordinaatsüsteem - reeglistik nimetatud arvude leidmiseks. Lihtsaim ja sagedamini kasutatav on ristkoordinaadistik (ka Descartes'i või Cartesiuse koordinaadid): kolm üksteisega risti olevat ühikvektorit, mille suunale projekteeritakse kirjeldatav kohavektor. Neid nn. baasivektoreid tähistatakse tähtedega $\vec i$, $\vec j$ ja $\vec k$ ning nad koos moodustavad ortonormaalse reeperi ("orto" tähendab siin ristseisu e. ortogonaalsust, "normaalne" aga seda, et vektorite pikkus on normeeritud väärtusega üks pikkusühik). Kui selline reeper on konstrueeritud, saab iga vektorit kirja panna kui kolme teljesuunalise vektori summat: $$\vec r=x\vec i+y\vec j+z\vec k$$ asendades raskestimõistetava kujundi $\vec r$ arusaadava tavaarvude kolmikuga $x,y,z$.	Reeper ja koordinaadid
Kuhu jäi taustkeha? Pole ta kuhugi kadunud - meie "reeperi" moodustabki taustkeha. Telgede suunad, ehkki suvaliselt valitud, jäävad edaspidi taustkeha suhtes paigale. Muidugi kulgeb kohavektor "punktist punkti" ja kirjeldab seega vaid uuritava keha kindla punkti liikumist taustkeha mingi kindla punkti suhtes. Aga kulgliikumise tarbeks sellest piisab: et liikumise määrab mitte kohavektor ise, vaid selle muutus ("nihe"), siis liiguvad samal kombel ka kõik uuritava keha ülejäänud punktid - ning seejuures taustkeha ükskõik millise punkti suhtes.	Kulgeval liikumisel liiguvad keha kõik punktid ühesugust teed mööda. Seepärast piisab ühe punkti liikumise kirjeldamisest.
Täpsuse huvides tasuks viimase lause üle järele mõelda.   Aja ja ruumi ühikud. Siin on paras aeg meenutada füüsikas kasutatavat ühikute süsteemi. Praegu enamlevinud mõõtühikute rahvusvaheline süsteem SI lähtub neljast põhiühikust, millest esimesed ongi ajavahemike pikkuse (kestuse) hindamiseks kasutatav sekund ja ruumilist ulatust väljendav pikkusühik meeter. Seejuures on ajaühik üldse "kõige põhilisem", ta on määratud loodusliku standardi - aatomisisese kvantülemineku energia - kaudu:	Aja ühik määratakse aatomisiseste võngete kestuse kaudu
Sekund on ajavahemik, mis on võrdne tseesiumi isotoobi $^{133}Cs$ põhiseisundi kahe peenstruktuuri nivoo vahelise ülemineku 9 192 631 770 perioodiga. Kus on siin energia? Aga tänapäeva (kvant)füüsikas määrabki sagedus energia(kvandi) suuruse. Ja samuti: aatomisisese ülemineku energia annab alati ühesuguse sageduse. See, miks on valitud just tseesium ja miks just kirjeldatud üleminek, on määratud tehnikaga: toodud skeemi on lihtsalt kõige odavam realiseerida. Pikkusühiku meetri saab määrata juba ajaühiku kaudu. Teades (relatiivsusteooriast!), et valguse kiirus on ühesugune kõigil planeetidel ja kõigis taustsüsteemides, määrataksegi meeter kui kindla aja jooksul valguse poolt läbitud tee:	Pikkuse ühiku määrab (aja kaudu) looduse universaalkonstant - valguse kiirus.
Meeter on vahemaa, mille valgus läbib vaakumis 1/299 792 458 sekundiga. Ja jälle on definitsiooni taga tehniline lahendus: kõige täpsemini saamegi pikkust määrata valguse lainepikkusega võrdlemise teel. Aga lainepikkus on tuletatav sagedusest ja valguse kiirusest. Meie jaoks on nii sekund kui meeter olemas vastavates erilaborites kontrollitud ning reguleeritud mõõteriistade kujul. Nii me kasutamegi mõõdulinti ja kella ning ei mõtle rohkem etaloonide (ühikuid määravate eeskirjade) peale.   Liikumisvõrrand. Keha asukoha sõltuvus ajast tähendab seda, et ülal toodud kohavektor tuleb anda sõltuvana ajast. Milline see sõltuvus täpselt on, tuleneb liikumise iseloomust. Oluline on see, et kui paneme liikumisvõrrandis argumendiks oleva aja tähise $t$ asemele mingi (positiivse või negatiivse) reaalarvu, peab võrrand andma meile keha asukoha (koordinaadid) sellele reaalarvule vastaval ajamomendil. "Liikumisvõrrand" kõrvale:	Liikumisvõrrand väljendab keha asukoha (kohavektori, st. selle kolme koordinaadi) sõltuvust ajast.
Seega on liikumisvõrrandiks vektorvõrrand $$\vec r(t)=x(t)\vec i+y(t)\vec j+z(t)\vec k,$$ kus $x(t)$, $y(t)$ ja $z(t)$ on kolm sõltumatut funktsiooni. Nii võiks liikumisvõrrandit käsitleda ka kui kolmest tavalisest võrrandist koosnevat võrrandisüsteemi. Klassikalises (Newtoni) mehaanikas antakse liikumisvõrrand tavaliselt kas teist järku diferentsiaalvõrrandi või ruutpolünoomi kujul. Neist esimene $$\ddot{\vec r}\equiv{{d^2\vec r}\over{dt^2}}={1\over m}\vec F$$ kujutab Newtoni II seadust, teine	Punkt muutujat tähistava tähe kohal märgib tuletist aja järgi; kaks punkti - teist järku tuletist aja järgi jne.
$$\vec r(t)=\vec{r_0}+\vec{v_0}\cdot t+{{\vec a}\over 2}\cdot t^2$$ tavalist koolifüüsika "ühtlaselt muutuva liikumise valemit", kus algasend $\vec r_0$, algkiirus $\vec v_0$ ning kiirendus $\vec a$ on antud vektorkujul. Et temast saaks tavaline võrrand, tuleb ta koordinaate pidi lahti kirjutada. Proovige.	NB! See on Teile antud ülesanne. Lahendage!
Mis vahe on neil kahel võrrandil? Kui on tegu "ühtlaselt muutuva liikumisega", st. kui kiirendus $a$ on konstantne - siis ei mingit. Ainult et tavaliselt kiirendus ei ole konstantne, kuna kehale mõjuv jõud pole peaaegu kunagi konstantne. Siis tuleb lahendada esimene võrrand. Või panna teise võrrandisse ajast sõltuv kiirendus, mis teeb sama välja ega pole ka lihtsam. Liikumisvõrrandi lahendamine kuulub dünaamikasse. Ja ega kinemaatika polegi mingi iseseisev mehaanika osa.
Pöörlemise võrrand.   Staatika ülesandes rääkisime ratta pöördumisest. Ka seda pöördumist saab mõõta, kasutades pöördenurka, mida mõõdab nurk pöörleva keha mistahes punkti pöördeteljega ühendava ristlõigu (nn. pöörlemisraadiuse) kahe eri ajamomendil määratud asendi vahel. Kui pöörleb tahke keha, on selle kõigi punktide pöördenurgad samad. Nii saame keha pööret kirjeldada üheainsa, pealegi veel skalaarse suurusega. Tähistades pöördenurga $\varphi$, nurk-kiiruse $\omega$ ning nurk-kiirenduse $\varepsilon$, saame kulgliikumisega analoogilise võrrandi: $$\varphi (t)=\varphi_0+\omega_0\cdot t+{{\varepsilon}\over 2}\cdot t^2.$$
Pöördenurga $\varphi$ ühikuna võib kasutada kõiki nurgamõõdu ühikuid, nagu kraad, radiaan, täispööre. SI-süsteemi ühikuks on radiaan:
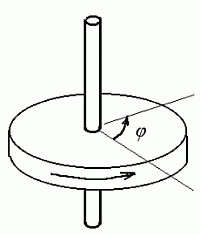
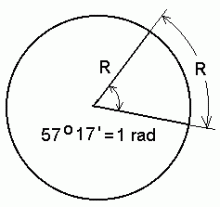
Radiaan on nurgamõõdu ühik, mis on võrdne ringjoone raadiuse pikkusele kaarele toetuva kesknurgaga. Üks täispööre võrdub $2\pi$ radiaaniga. See on väga mugav ühik, kui meil on tarvis leida pöörleva keha mistahes punkti joonkiirust. Kui pöördenurka mõõta radiaanides, tuleb nurkkiiruse ühikuks "radiaani sekundi kohta" (rad/s või lihtsalt 1/s - radiaan kui kaare pikkuse ja raadiuse pikkuse suhe on tegelikult dimensioonita suurus). Et saada joonkiirust (kiirust, millega liigub pöörleva keha mingi punkt), tuleb nurkkiirus korrutada vaadeldava punkti kaugusega pöördeteljest.	Radiaan on ringjoonele joonistatud kesknurk, millele vastava kaare pikkus on võrdne selle ringjoone raadiusega.
Pöördenurga märgist. Keha saab teljel pöörata kas ühele või teisele poole. Üht neist pöördeist tuleks lugeda positiivseks, teist negatiivseks. See tuleb jällegi kokku leppida. Ja kokkulepe on nii, et positiivseks loetakse pööre vastu kellaosuti liikumise suunada. See on lihtne vaid paberile joonistatult. Kui vaadata pöörlevat keha ruumis ühelt poolt, näeme teda pöörlevana üht, teiselt poolt vaadatuna aga teistpidi. See, kummalt poolt vaadatakse, määratakse teljele kantud suuna -- pöörlemisvektori -- abil. Aga sellest hiljem, tahke keha liikumist kirjeldavas osas.	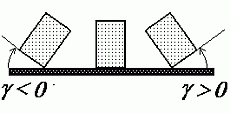Pöördenurga märk sõltub pöörde suunast
Liikumisvõrrandi diferentseerimine. Liikumisvõrrandis on antud keha asukoht (kohavektor) sõltuvalt ajast. Newtoni järgi on see funktsioon pidev, järelikult võib liikumisvõrrandit diferentseerida. Liikumisvõrrandi esimest tuletist aja järgi nimetatakse kiiruseks. See näitab, kui kiiresti liigub keha antud ajahetkel. Liikumisvõrrandi teist tuletist aja järgi (kiiruse esimest tuletist) nimetatakse kiirenduseks. Kiirendus näitab kiiruse muutumise kiirust antud ajahetkel. Joont, mis ühendab keha asukohti järjestikustel ajamomentidel, nimetatakse keha trajektooriks. Keha liigub ruumis piki trajektoori. Trajektoor on sile joon; temas ei ole katkevusi ja muid iseäralikke punkte. Kiirusvektor on trajektoorile alati puutujaks, ta näitab liikumissuunda. Kiirendusvektor seevastu võib olla trajektoori suhtes ka nurga all. Ta on seda alati, kui keha liigub piki kõverjoont. Et kõverjooneline liikumine tähendab liikumissuuna muutust, peab sellega kaasnema kiirusvektori muutumine isegi siis, kui kiiruse väärtus (vektori moodul) ei muutu. Liikumissuuna muutust põhjustavat kiirenduse komponenti nimetatakse normaalkiirenduseks ja ta on alati kiirusvektoriga (seega ka trajektooriga) risti. Kiirenduse liikumissuunalist (kiirusvektoriga samas sihis olevat) komponenti nimetatakse tangentsiaalkiirenduseks (ingl.,lad., tangent -- puutja). Ülesanne: püüdke kirjeldada suurusi, mis tekivad pöördliikumise võrrandi diferentseerimisel.	Keha liikumissuunda näitab kiirusvektor. Kui kiirusvektori suund liikumise käigus muutub, nimetatakse liikumist kõverjooneliseks. Kiirusvektori komponendid

* Sisukorda *