Loeng 19. Kiirgusoptika
Valguse vastasmõju keskkonnaga. Elektromagnetlainetest
rääkides oleme korduvalt rõhutanud, et need ei vaja oma levimiseks
keskkonda. Tavaväide on selline, et tegu on ruumis leviva
elektri- või magnetväljaga, mille tugevus muutub vastavalt
lainevõrrandile. Küsimusele, mida selline "väli" endast kujutab,
vastatakse tavaliselt Newtoni füüsika laadis: väli (täpsemalt
jõuväli) on matemaatiline abstraktsioon, mis lubab kirjeldada kehade
vastasmõju ruumikoordinaatidest sõltuvate funktsioonide
(väljatugevus, potentsiaal) vahendusel.
Kõik see on õige staatiliste väljade (gravitatsiooniväli,
elektriväli) korral. "Laineline" elektromagnetväli on sootuks teist
tüüpi füüsikaline objekt. Staatilise välja tekitamiseks
ei kulu energiat - see kuulub kehade teatud omaduste (mass,
elektrilaeng) juurde. Et tekitada elektromagnetlaineid (valgust),
tuleb aga teha tööd, st. kulutada energiat. Ka on võimalik neist
lainetest energiat ammutada (näiteks end päikese käes soojendades).
|
Valgus (elektromagnetväli) kujutab endast ruumis levivat energiavoogu, mida kirjeldab lainevõrrand.
Vastasmõjus ainega võib valgus
neelduda,
hajuda,
peegelduda,
murduda (muuta faasikiirust) ja
polariseeruda (muuta võnketasandit).
|
|
Kiirgusoptika käsitleb valgust (elektromagnetlaineid) kui
energiavoogu.
Vastasmõjus ainega (keskkonnaga) võib see energia
- neelduda (muutudes teisteks energialiikideks),
- hajuda
(muutudes mingis teises suunas levivaks kiirguseks),
- peegelduda
või murduda, (muuta suunda või levimiskiirust),
- polariseeruda
(muuta võnketasandit) ja isegi
- jaguneda kaheks eri suunas levivaks
kiirguseks (kaksikmurdumise korral).
Sellesse teemasse kuulub ka
kiirguse teke.
Kaasaegses füüsikas käsitletakse kõiki neid probleeme
kvant-teooria seisukohalt. Meie ülesandeks on kõigepealt jõuda
laineoptikast kvant-teooriani. Aga alustame siiski klassikalise
laineteooriaga.
Ostsillaatoritest koosnev keskkond. Kõige lihtsam viis kirjeldada laine
levikut keskkonnas on oletada, et keskkond koosneb
võnkumisvõimelistest osakestest - nn. ostsillaatoritest.
Ostsillaatori omadused tulenevad võnkumiste võrrandist ja neid
saab väljendada kahe parameetriga: omavõnkesagedus
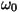 ja sumbuvustegur ja sumbuvustegur 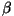 . Mis moel need kaks
sõltuvad keskkonna omadustest, seda me ei vaata. . Mis moel need kaks
sõltuvad keskkonna omadustest, seda me ei vaata.
|
Laineoptikas käsitletakse keskkonda kui võnkumisväimeliste osakeste - ostsillaatorite kogumit.
NB! Järgneva teksti matemaatiline osa pole Teie jaoks kohustuslik materjal, vaid pigem illustratsioon selle kohta, kuhu jõudis klassikaline füüsika 19. sajandi lõpuks.
|
|
Ostsillaatori liikumisvõrrand on meile juba tuttav
sumbuvvõnkumiste võrrand:
|
Klassikaline füüsika kirjeldab valguse vastasmõju ainega ostsillaatorite sundvõnkumise kaudu: elektromagnetväli paneb ostsillaatori võnkuma, võnkuv ostsillaator aga käitub laineallikana.
|
ehk komplekskujul
Elektromagnetlaine levimisel keskkonnas hakkab ostsillaator
sooritama sundvõnkeid temale mõjuva perioodilise jõu
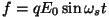 toimel. Nagu võnkumiste teooriast teada, toimuvad
need sundiva jõu sagedusega ( toimel. Nagu võnkumiste teooriast teada, toimuvad
need sundiva jõu sagedusega (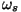 ), aga faasinihkega ), aga faasinihkega
Amplituud meid üldjuhul ei huvita. Võnkuvat ostsillaatorit
vaatame nüüd kui Huygens'i lainefrondi punkti - sekundaarlaine
allikat. See tähendab, et laine levimisel keskkonnas kasutame
todasama Huygens-Fresnel'i printsiipi, arvestades täiendavalt
faasinihet ja vajaduse korral ka amplituudi muutumist.
See on loomulikult klassikalise mehaanika vaatenurk.
Tänapäeva füüsikas on ostsillaator ennekõike kvantobjekt.
|
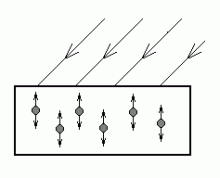
Keskkonnas leviva valguse klassikaline mudel:
muutuvas elektriväljas võnkuvad laenguga osakesed - ostsillaatorid.
Kaasaegses füüsikas on ostsillaator kvantobjekt, mille olekut (olekuparameetrite komplekt kuhu kuulub ka energia) kirjeldavad spetsiaalsed suurused - kvant-arvud.
|
|
Valguse murdumine (faasikiiruse muutus).
Vaatame, kuidas mõjutab valguslaine levimist tema teele asetatud
õhuke plaat paksusega 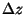 ja murdumisnäitajaga ja murdumisnäitajaga 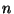 .
Plaadile langev valguslaine sisaldab harmooniliselt muutuvat
elektrivälja .
Plaadile langev valguslaine sisaldab harmooniliselt muutuvat
elektrivälja
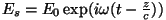 . Koosnegu
keskkond ostsillaatoritest laenguga . Koosnegu
keskkond ostsillaatoritest laenguga 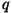 , massiga , massiga 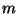 ja
omavõnkesagedusega ja
omavõnkesagedusega 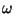 . Sumbuvust (amplituudi muutust) me
esialgu ei vaata. . Sumbuvust (amplituudi muutust) me
esialgu ei vaata.
Sundvõngete teooria järgi hakkab harmooniliselt muutuvasse
elektrivälja sattunud ostsillaator tegema sundvõnkeid
amplituudiga
ja sagedusega 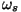 . Selle tagajärjel hakkab ta kiirgama
keralainet. Kaugusel . Selle tagajärjel hakkab ta kiirgama
keralainet. Kaugusel  on tema poolt tekitatud elektrivälja tugevuse valem on tema poolt tekitatud elektrivälja tugevuse valem
|
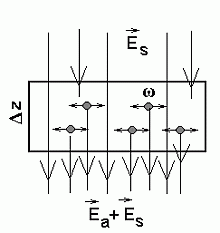
Võnkuv elektriväli läbipaistva plaadi taga:
esialgsele lainele 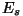 lisandub ostsillaatorite genereeritud laine
lisandub ostsillaatorite genereeritud laine 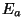 . .
|
Küsimus: Miks on nimetajas 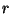 , mitte aga , mitte aga 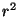 ? Mõelge välja! ? Mõelge välja!
Et saada summaarset kiirgust punktis 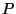 , tuleb liita kõigi
ostsillaatorite kiirgused. Olgu ostsillaatorite ruumtihedus , tuleb liita kõigi
ostsillaatorite kiirgused. Olgu ostsillaatorite ruumtihedus 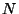 osakest kuupmeetris. Jagame keskkonna tasapinnalise plaadi kujulisteks kihtideks, iga sellise kihi omakorda pinnaelementideks. Pinnaelemendilt
osakest kuupmeetris. Jagame keskkonna tasapinnalise plaadi kujulisteks kihtideks, iga sellise kihi omakorda pinnaelementideks. Pinnaelemendilt 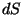 lähtub sel juhul
kiirgus lähtub sel juhul
kiirgus
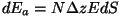 . Integreerime kihtide kaupa,
kasutades "summeerimist üle rõngaste". . Integreerime kihtide kaupa,
kasutades "summeerimist üle rõngaste".
Teeme muutuja vahetuse:
Saame
Et
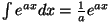 , saame , saame
|
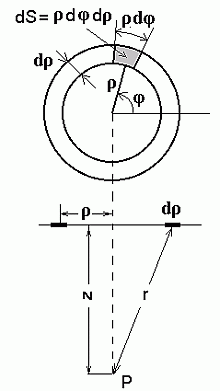
Plaadilt lähtuva laine arvutamine - summeerimine üle rõngaste.
|
Mäletatavasti
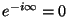 . Et . Et 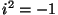 , siis , siis
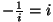 , nii et , nii et
Kuna plaadi taguses ruumis levib jätkuvalt ka esialgne laine, koosneb laine
teisel pool plaati kahest liidetavast:
Näeme, et mõlemad lained on sagedusega 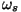 ja levivad
kiirusega ja levivad
kiirusega 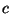 . Ainult et liitlaine amplituudiks on kompleksarv.
Komplekstasandil kujutab seda arvu meile juba tuttav faasidiagramm. . Ainult et liitlaine amplituudiks on kompleksarv.
Komplekstasandil kujutab seda arvu meile juba tuttav faasidiagramm.
Kuidas sellest aru saada? Tuletame meelde vahelduvvooluahelate
vektordiagramme. Laine (võnkumine) tähendab seda, et
amplituudivektor pöörleb kellaosutile vastassuunas nurkkiirusega
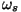 . Et kiirused olid võrdsed, pöörlevad nii . Et kiirused olid võrdsed, pöörlevad nii 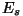 kui kui
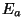 koos; koos nendega loomulikult ka vektorsumma koos; koos nendega loomulikult ka vektorsumma 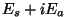 . .
|
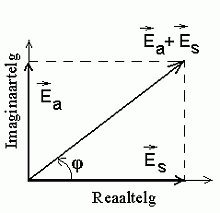
Faasinihe
primaarse laine (vektor 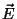 ) ja ostsillaatori kiiratud sekundaarlaine (vektor ) ja ostsillaatori kiiratud sekundaarlaine (vektor 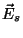 ) vahel. ) vahel.
|
Ainult et see summaarne väljavektor jääb esialgsest väljast
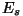 maha nurga maha nurga 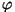 võrra. Ja seda nurka saab arvutada: võrra. Ja seda nurka saab arvutada:
Seega liitlaine hilineb faasis, säilitades seejuures endise
sageduse ja levimiskiiruse. Viimane tundub imelikuna - oleme
juba jõudnud harjuda Fermat' printsiibi ning kiiruse
vähenemisega.
Aga: me vist unustame, mille me leidsime: meie
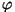 tähendab faasi hilinemist ja see hilinemine on
võrdeline kihi paksusega tähendab faasi hilinemist ja see hilinemine on
võrdeline kihi paksusega 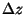 . Kokkuvõttes: faasi
hilinemine polegi muud, kui faasikiiruse vähenemine. . Kokkuvõttes: faasi
hilinemine polegi muud, kui faasikiiruse vähenemine.
|
Ostsillaatorite poolt põhjustatud faasinihe on samaväärne laine levimiskiiruse (faasikiiruse) muutumisega.
|
|
Võrdleme saadud tulemust faasikiiruse harjumuspärase valemiga
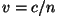 . Faasi hilinemiseks kihis paksusega . Faasi hilinemiseks kihis paksusega 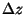 tuleb: tuleb:
Väikese 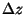 korral, arvestades korral, arvestades 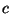 suurt väärtust, võime
lugeda suurt väärtust, võime
lugeda
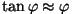 . Võrreldes faasinihke kaht valemit,
saame murdumisnäitaja "teoreetilise väärtuse": . Võrreldes faasinihke kaht valemit,
saame murdumisnäitaja "teoreetilise väärtuse":
Näeme, et murdumisnäitaja ühele liituv osa koosneb konstantsest
kordajast (on atomaarsete konstantide kombinatsioon) ja
liikmest, mille väärtus sõltub valguse sagedusest.
Viimase muutumist iseloomustab kõrvaltoodud graafik.
|
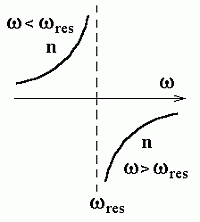
"Teoreetiline dispersioon":
faasinihke kõverad kahel pool resonants-sagedust. Hea tahtmise juures leiab siit isegi mingi sarnasuse eksperimentaalsete kõveratega...
|
Üldiselt on
pilt selline, et läbipaistvates ainetes on omasagedus
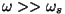 . Seetõttu on neis . Seetõttu on neis 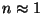 (ulatub
maksimaalselt kolmeni). Kuna vasakul pool resonantsijoont
( (ulatub
maksimaalselt kolmeni). Kuna vasakul pool resonantsijoont
(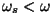 ) on murdumisnäitaja suurem ühest, tuleb
liitlaine faasinihe negatiivne ja seetõttu faasikiirus väheneb.
Paremal pool resonantsipiirkonda oleks pilt vastupidine: ) on murdumisnäitaja suurem ühest, tuleb
liitlaine faasinihe negatiivne ja seetõttu faasikiirus väheneb.
Paremal pool resonantsipiirkonda oleks pilt vastupidine: 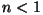 ,
faasinihe positiivne ja ,
faasinihe positiivne ja 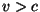 . .
Kõik see ei tähenda midagi valguse tegeliku kiiruse kohta.
Elektriväli, olgu ta muutlik või muutumatu, levib ruumis
kiirusega 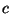 . Meie poolt "valguse kiirusena" käsitletav
faasikiirus määrab vaid lainevektori, st energiavoo suuna. Suuna
muutus keskkondade eralduspiiril seostub ainult faasikiirusega,
nagu järeldus juba Fermat' printsiibist. . Meie poolt "valguse kiirusena" käsitletav
faasikiirus määrab vaid lainevektori, st energiavoo suuna. Suuna
muutus keskkondade eralduspiiril seostub ainult faasikiirusega,
nagu järeldus juba Fermat' printsiibist.
|
|
|
Dispersioon. Meie poolt leitud murdumisnäitaja
sõltuvus sagedusest (lainepikkusest) kannab nimetust dispersioon
(lad. dispersio = hajumine). Levinuimat juhtu, kus
sageduse suurenemisel 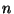 kasvab, nimetatakse normaalseks,
vastupidist ( kasvab, nimetatakse normaalseks,
vastupidist (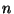 kahaneb) aga anomaalseks dispersiooniks. kahaneb) aga anomaalseks dispersiooniks.
|
Faasikiiruse sõltuvust sagedusest (millest järeldub erineva lainepikkusega kiirguse erinev murdumisnäitaja) nimetatakse dispersiooniks.
|
Normaalse dispersiooni korral murduvad sinised kiired (lühem
lainepikkus, järelikult suurem sagedus) rohkem kui punased:
seetõttu paiknevad prismaspektroskoobis spektrivärvid
vastupidiselt difraktsioonimaksimumile, kus rohkem kaldusid
kõrvale just punased kiired.
Dispersiooni teooria on kvalitatiivne, täpseid valemeid ei saa
me isegi kvantteooria abiga. Praktikas kasutatakse
lähendvalemeid (rittaarendusi), nagu:
piirdudes tavaliselt kahe esimese liikmega. Dispersioonil
põhinevaid spektraalriistu kalibreeritakse tavaliselt töö
käigus.
|
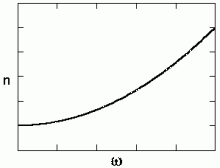
Dispersioon arvutatuna "astmerealise" lähendvalemi järgi.
|
|
Neeldumine. Ülaltoodud matemaatilistes arutlustes
vältisime teadlikult sumbuvustegurit 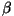 . Tegelikult
sisaldab sundvõngete valem alati neeldumisliiget, mis muudab nii amplituudi kui faasinihke valemite kuju: . Tegelikult
sisaldab sundvõngete valem alati neeldumisliiget, mis muudab nii amplituudi kui faasinihke valemite kuju:
Viimaseid võime kompleksesituses anda ka ühe valemina:
|
|
Imaginaararvuline sumbuvusliige 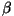 sisaldub ainult nimetaja sulgavaldises ja
seetõttu võime defineerida kompleksarvulise "murdumisnäitaja": sisaldub ainult nimetaja sulgavaldises ja
seetõttu võime defineerida kompleksarvulise "murdumisnäitaja":
Selle reaal- ja imaginaarosa avalduvad kujul:
Proovime nüüd avaldada väljavõrrandit teisel pool plaati.
Analoogia põhjal murdumist käsitleva osaga saame
kus
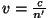 . .
|
Sumbuvusteguri sissetoomine ostsillaatori sundvõngete võrrandisse kajastub väljatugevuse valemis eksponent-tegurina, mille astendaja on negatiivne ning võrdeline valguse tee pikkusega keskkonnas.
|
Näeme, et "murdunud lainele" lisandus
tegur
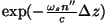 , kus kihi paksust
väljendava , kus kihi paksust
väljendava 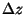 kõrval on kõik ülejäänud suurused
konstantsed. kõrval on kõik ülejäänud suurused
konstantsed.
|
Diferentsiaalvõrrandite teooriast:
kui mingi funktsiooni tuletis on võrdeline tema endaga, siis sisaldab otsitav funktsioon alati eksponent-tegurit.
|
Negatiivne eksponent lainevõrrandis tähendab amplituudi
vähenemist, see aga kajastub laine intensiivsuse vähenemises. Et
intensiivsus on võrdeline amplituudi ruuduga, saame valemi
kus
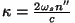 kannab
neeldumisteguri nime. Kokku saime nn. Bouguer' (loe: buzee) seaduse, mis kirjeldab valguse nõrgenemist neelavas
keskkonnas.
Näeme, et neeldumistegur sõltub vahest kannab
neeldumisteguri nime. Kokku saime nn. Bouguer' (loe: buzee) seaduse, mis kirjeldab valguse nõrgenemist neelavas
keskkonnas.
Näeme, et neeldumistegur sõltub vahest
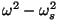 ja
on maksimaalne resonantsipiirkonnas ja
on maksimaalne resonantsipiirkonnas
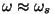 . .
|
Valguse intensiivsuse kahanemine eksponentfunktsiooni järgi on tuntud Bouger' neeldumisseaduse nime all.
|
|
Seetõttu
- pole ained resonantsipiirkonnas läbipaistvad ja
- murdumisnäitaja ja faasikiirus ei omanda kunagi lõpmatut
väärtust.
Muide on olemas ka teisi meetodeid dispersiooni ja neeldumise
teoreetiliseks põhjendamiseks (vt. näit. I.Saveljev, Füüsika III, 7. ptk.).
Ma valisin R. Feynmanni interpretatsiooni kui mulle teada
olevaist kõige kompleksema. Tema abil saadakse jagu ka
polarisatsioonist.
Mis saab "kadunud energiast"? Aine loomulikult soojeneb - see
on üks võimalus. Aga ta võib ka valgust hajutada. Kvantfüüsika
lubab väga mitmesuguseid hajumismehhanisme; ja mõned neist on
reaalselt jälgitavad.
(Vt: Rayleigh' hajumine, Tyndall'i efekt, Comptoni efekt,
kombinatsioonhajumine, fotoluminestsents - I. Saveljev. Füüsika III).
|
Tähelepanu! Polarisatsiooninähtuste all mõistetakse laineoptikas vaatluslikke fakte, mida saab kirjeldada muutuva elektrivälja valikulise suunaga. Kõik käesoleva osa joonised on tehtud sellest definitsioonist lähtuvalt.
|
|
Polarisatsioon. Seni vaatasime nii ostsillaatorit kui
lainet mingi abstraktse võnkumisena. Tegelikult on
harmoonilistel võngetel alati määratud võnkesiht (siht või
telg, mille suunas toimub võnkuva keha liikumine) ja ristlaine
korral ka võnketasand (tasand läbi võnkesihi ning
lainevektori).
Polarisatsiooni all mõistetakse optikas nähtusi, mida saab
seletada valguse kui ristlainetuse sõltuvusega võnketasandist.
Eristatakse loomulikku valgust, kus valguskiires
(lainepaketis) on võrdselt esindatud kõik võimalikud
võnketasandid.
- Kui mingi tasand on eelistatud, räägime
osaliselt polariseeritud valgusest.
- Kui elektrivälja tugevus
muutub ainult ühes kindlas sihis, on valgus täielikult e.
lineaarselt polariseeritud.
|
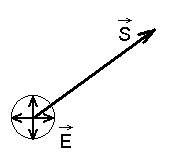
Polariseerimata ehk "loomulik" valgus.
Väljavektor 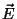 on laine liikumissuunaga ristuvas tasandis, eelissuund aga puudub (kõik suunad on võrdselt esindatud).
on laine liikumissuunaga ristuvas tasandis, eelissuund aga puudub (kõik suunad on võrdselt esindatud).
|
|
See, missuguse valgusega on
tegemist, sõltub nii valgusallika omadustest kui ka keskkonnast,
milles valgus levib. Looduslike valgusallikate korral on
tavaliselt tegu loomuliku, polariseerimata valgusega.
Valguse polariseeritust pole võimalik kiirgusvastuvõtjate abil
mõõta, kuna valgsvoo energeetilised näitajad võnketasandist ei
sõltu. Seetõttu kasutatakse polarimeetrites spetsiaalseid
valgusfiltreid, nn. polaroide, mis lasevad läbi ainult
kindla võnketasandiga kiirgust. Pöörates sellist filtrit
kiirgusvastuvõtja või lihtsalt silma ees, on võimalik heleduse
perioodilise muutumise järgi kindlaks teha ja ka mõõta
polarisatsiooni olemasolu.
|
Polarisatsiooni saab kindlaks teha polaroidiga - seadmega, mis laseb läbi ainult kindlas suunas polariseeritud valgust. Polaroidi läbinud valgus on alati lineaarselt polariseeritud.
|
Mõõdetavaks suuruseks on nn.
polarisatsiooniaste:
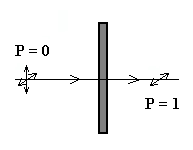
Näeme, et polariseerimata valguse
(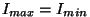 ) korral on ) korral on
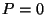 , lineaarselt polariseeritud valgusel ( , lineaarselt polariseeritud valgusel (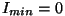 ) aga ) aga
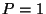 . .
Tegelikult ei tähenda nulliga võrdne polarisatsiooniaste veel
polarisatsiooni puudumist. Kujutame näiteks kaht koherentset,
lineaarselt polariseeritud, sama intensiivsusega, samas suunas
levivat kiirt, mille käiguvahe on näiteks 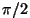 . Polarisaatori
läbib selline valgus nagu loomulik; aga sellele vaatamata on
tegu "ebaloomuliku", seekord ringpolariseeritud valgusega. . Polarisaatori
läbib selline valgus nagu loomulik; aga sellele vaatamata on
tegu "ebaloomuliku", seekord ringpolariseeritud valgusega.
Kui kiirte intensiivsused on erinevad või faasinurk erinev
täisnurgast, on tegu elliptiliselt
polariseeritud valgusega.
Looduses esineb ka aineid, milles levimisel
valguse polarisatsioonitasand muutub - neid nim.
optiliselt aktiivseteks aineteks ja enamik neist on orgaanilise
päritoluga ühendid (näit. suhkur).
Vaatame järgnevalt võimalikke seletusi mõningaile
polarisatsiooninähtustele. Ette võib öelda, et täielikku
seletust kõigile neile füüsika ei tunne.
Lähtume kujutlusest, et
valgus on ristlainetus,
kehtib Huygens-Fresnel'i printsiip ja
keskkond, milles valgus levib, koosneb kindlate omadustega
ostsillaatoritest.
|
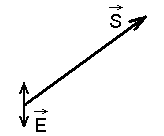
Täielikult e. lineaarselt polariseeritud valgus.
Lubatud on ainult üks kindel võnkesiht.
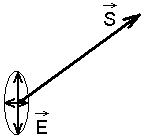
Osaliselt polariseeritud valgus.
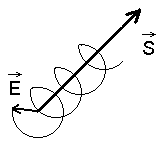
Ringpolariseeritud valgus.
Elektrivälja vektori "ots" joonistab lainevektori ümber spiraali.
|
|
A. Polarisatsioon hajumisel. Vaatleme mittehomogeenses
(hägusas) keskkonnas levivat tasalainet. Laine teele jäävad
ostsillaatorid võnguvad võnkesihis; seetõttu on nende poolt
kiiratud valgus polariseerimata vaid "piki lainet", st.laine levimise
sihis.
Kui esineb hajumine (ostsillaatorid või nende rühmad kiirgavad
mingis muus suunas), siis ei saa see valgus olla polariseerimata. Kui
oletada, et ostsillaatori kiiratud valguse polarisatsioonitasand on
paralleelne võnkesihiga, peaks kiire suunast täisnurga all hajunud
kiirgus olema lineaarselt, ülejäänud nurkade korral aga
osaliselt polariseeritud.
Mõõtmised näitavad, et efekt on olemas, ehkki mitte absoluutne: me ei arvestanud korduva hajumise võimalust.
Võtame näiteks päevase
taeva. Selle sinine värv osutab
molekulaarsele (Rayleigh') hajumisele ja polarisatsioon on hästi
järgitav. Räägitakse, et umbes 5% inimestest eristab
polariseeritud valgust tavalisest, tajudes teda kollaka
värvusena. Minul pole au nende hulka kuuluda, aga igaüks võib
seda proovida. Vaadake sinisesse taevasse umbes 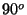 nurga all
Päikesest ja kui näete vertikaalset kollast vööti, võite uskuda,
et see ongi polarisatsioonist tingitud värvimuutus. nurga all
Päikesest ja kui näete vertikaalset kollast vööti, võite uskuda,
et see ongi polarisatsioonist tingitud värvimuutus.
|
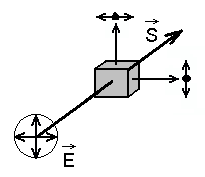
Polarisatsioon hajumisel:
täisnurga all hajunud valgus peab olema polariseeritud, kuna ostsillaatorid võnguvad esialgse kiire suunaga risti.
|
|
B. Polarisatsioon peegeldumisel. Sama nähtus tuleb esile
ka valguse peegeldumisel keskkondade eralduspinnalt. Siingi
võnguvad ostsillaatorid ainult risti kiirega. Keskkondade
eralduspinnal kiir murdub ja kuna "alumise" keskkonna ostsillaatorid
peavad samuti võnkuma
risti murdunud kiirega, jääb osa võnkumist "üle". See "ülejäänud"
valgus ei saa kuhugi kaduda ning ainsaks võimaluseks on peegeldumine
murdvalt pinnalt tagasi "ülemisse" keskkonda.
Tekib kaks polariseeritud kiirt: peegeldunud kiires on ülekaalus
pinnaga paralleelsed, murdunud kiires aga pinnaga ristuvad
võnkumised. Juhul, kui peegeldunud ja murdunud kiir on omavahel
risti, on valgus peegeldunud kiires täielikult (lineaarselt) polariseeritud.
Langemisnurka, mille korral murdunud ja peegeldunud kiir
moodustavad täisnurga ja peegeldunud kiir on täielikult
polariseeritud, nim. Brewsteri nurgaks. Loomulikult on
siis polariseeritud ka murdunud kiir - aga mitte täielikult!
Küsimus: Kas oskate seletada, mispärast?
Kui murdvale pinnale langeb polariseeritud valgus, on täheldatav
peegeldunud kiirguse intensiivsuse langus Brewsteri nurga
lähedal. See annab võimaluse näha sinitaeva valguse
polariseeritust ka "normaalse" nägemisega inimestel. Vaadake
taeva peegeldust vees õige nurga all ja leidke üles tume laik.
|
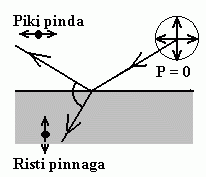
Polarisatsioon peegeldumisel.
Ostsillaatorid peegelpinnal ei saa võnkuda risti pinnaga - peegeldunud kiir peab olema polariseeritud.
|
|
C. Polarisatsioon anisotroopses kristallis. Oma
rehkendustes oletasime, et ostsillaatori omasagedus ei sõltu
suunast. See on õige vedelikes ja amorfsetes ainetes (nagu
klaas), aga mitte kristallides.
Telgsümmeetrilistes
kristallides, nagu pagu, kvarts jt. on tavaline, et
omavõnkesagedus peatelje sihis erineb sagedustest sellega
ristuvates suundades. Meie teooria järgi kajastub see
faasikiiruse, seega ka murdumisnäitaja erinevuses.
Seetõttu võib
juhtuda, et peatelje sihis polariseeritud valgus murdub
ülejäänuist erineva nurga all. Tulemuseks on see, et kristallile
langev kiir jaguneb kaheks ristuvates tasandeis lineaarselt
polariseeritud kiireks. Nähtus avastati 1670. a. islandi pao
kristalli juures; suuremal või väiksemal määral on see mõõdetav
kõigi mittekuubilise sümmeetriaga kristalsetel ainetel.
Kaksikmurdumise juures on tähelepanuväärne see, et murduda võib
ka pinnale risti langev kiir. Mõelge, millistel tingimustel see
juhtub ja põhjendage nähtust Huygensi printsiibi abil.
|
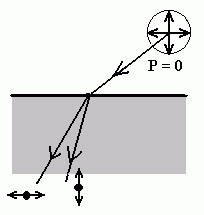
Kaksikmurdumise seletamine polarisatsiooniga.
|
|
D. Polarisatsioon neeldumisel. Mis juhtub, kui
anisotroopse kristalli ühe telje suunas on mingi lainepikkusega
valgus resonantsolukorras, teiste telgede suhtes aga mitte. Juhtub
see, et "neelava telje" sihis võnkuv kiirgus neeldub,
ülejäänu aga levib rahulikult läbi kristalli.
Saame jällegi
polariseeritud valguse, nüüd aga tänu selektiivsele
neeldumisele.
Polaroidid. Aineid, mis neelavad kindlas sihis polariseeritud valgust,
nimetasime polaroidideks. Parimad polaroidid kujutavad endast
niitjate kristallide (või polümeerset tüüpi molekulide) kogumit,
kus võnkumised piki kristalli on praktiliselt vabad (toimub
tugev neeldumine), risti kristalliga aga keelatud (neeldumine
puudub).
|
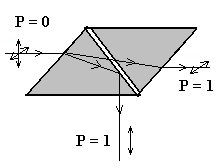
Nicol'i prisma (nikol)
- kaksikmurdumisel põhinev seade, mis jagab loomuliku valguse kaheks ristsuunas levivaks, lineaarselt polariseeritud kiireks..
|
|
Polarisatsioon tehnikas. Polaroidide kasutusalade
loetlemine pikendaks meie kursust vähemalt ühe täisloengu võrra.
Lisan vaid, et ainete optilised omadused, ka polariseeriv toime,
on sõltuvad välistingimustest. Nii täheldatakse optilise
anisotroopia teket mehaanilisel deformatsioonil, magnetvälja
toimel (Faraday efekt) ja elektriväljas (Kerri efekt). Et
optilised mõõtmised on võrratult lihtsamad mehaanilistest, on
siin üht-teist inseneridele.
Kõige viljakamaid rakendusi on
andnud Kerri efekt - just see võimaldab konstrueerida
päikesepatareidel töötavaid kalkulaatoreid ja viieaastase
patareiga käekelli.
Vedelkristallindikaator - nn. Kerr'i rakk
- on praktiliselt energiavaba indikaator. Ta koosneb
peegelpinnale kantud aktiivaine kihist, mida katab polaroid.
Staatilise välja lülitumisel (voolu, seega ka energiat pole
vaja!) pöördub polaroidi läbinud valguse võnketasand tema ja
peegli vahelises aktiivaines, mistõttu valgus enam läbi ei
pääse.
Lülitatud pingega element paistab ekraanil tumedana;
neist võib moodustada nii numbreid kui pilte. Kerri rakk lülitub
äärmiselt kiiresti, see lubab ekraani kasutada ka liikuvate
piltide näitamiseks.
|

Vedelkristall-indikaator - Kerr'i rakk.
|
|
Keskkond kiirgajana. Valgusallikatest rääkides oleme
senini toetunud kogemusele, et sellised asjad on olemas. Oleks
juba aeg rääkida põhjustest, miks valgus tekib - ehk
täpsemalt väljendudes tingimustest, millal kehad
kiirgavad.
Valgus (ja igasugune , ka elektromagnetlaine) kannab energiat,
kujutades endast energiavoogu. Seetõttu peab kiirgusallikas seda
energiat tootma. Usume, et iseenesest energia ei teki;
järelikult
valgusallikas toimub mingite teiste
energialiikide muutumine valguskiirguseks.
Füüsika tunneb üsna
palju selliseid energia muundumise liike, aga 99.9% valgusest
tekib looduses ja tehnikas aineosakeste soojusliikumise
arvel. Seda kuumutatud kehade kiirgust nimetatakse
soojuslikuks kiirguseks e. lühemalt soojuskiirguseks
(mitte segi ajada infrapunase kiirgusega, mida mõnikord samuti
soojuskiirguseks nimetame).
|
Valgus ei teki iseenesest; kiirgajateks on aineosakesed, mille (sise)energia muundub valguseks.
Kui kehade poolt kiiratav valgus tekib soojusliikumise arvel, nimetatakse tekkivat kiirgust soojuskiirguseks.
|
|
Luminestsents ehk "külm valgus". Enne, kui asuda soojuskiirguse valemite
tuletamisele, paneme lühidalt kirja põhilise, mis eristab teisi
kiirguse liike. Soojuskiirguse intensiivsus sõltub keha
temperatuurist ja pinna omadustest; kui mingi keha kiirgab
rohkem, kui ta peaks kiirgama antud temperatuuril, on tegemist
luminestsentsiga (lad. 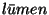 = valgus). = valgus).
|
Mittesoojusliku tekkemehhanismiga kiirgusi nimetatakse üldnimega luminestsents.
|
|
"Normaalsest" madalama temperatuuri tõttu nimetatakse
luminestsentsi ka külmaks valguseks.
Luminestsentsi põhjused peituvad aine ehituses. Mõnikord eraldub
valguse kujul keemiliste reaktsioonide käigus eralduv energia -
seda nähtust nim. kemoluminestsentsiks. Viimase
alamliigiks on bioluminestsents - mõnede organismide
helendumine, tavaliselt liigisisese signalisatsiooni eesmärgil.
Kui siia lisada veel teatud ainete võime valgust "salvestada",
st. pärast valgustamist jätkata kiirgamist teatud aja vältel
(nim. fosforestsentsiks, kuna nähtust täheldati kõigepealt
fosforiühendite juures), ongi looduslik luminestsents
ammendatud.
Tehnika tunneb aga veel mõnesid luminestsentsi alaliike. Näiteks noortemoes tooni andvad erksad värvid
põhinevad fotoluminestsentsil e. fluorestsentsil (viimane
nimetus tuleneb asjaolust, et nende ainete hulgas on rohkesti
fluoriühendeid). Eriti hämaras valguses silma torkav helendumine
on põhjustatud nende värvainete omadusel teisendada kogu temale
langev kiirgus kindlasse spektrivahemikku.
Seejuures kehtib
(kvantmehaanika) seadus, et neeldunud valguse lainepikkus peab
olema väiksem kiirguva omast. Jälgige teile armsaid
pluusikesi-mütsikesi - hõõglambi kollases (suure
lainepikkusega) valguses tuhmuvad kõik sinised-rohelised toonid
ja ainsana helendub nn. signaalpunane (mis oli üldse esimene
kasutusele võetud fluorestsent). Seevastu päevavalguses ja
luminestsentslampide all on kõige erksamad just sinised
toonid.
Tunneme veel
radioluminestsentsi (helendumine
kiirete osakeste, näit, elektronide voo mõjul),
elektroluminestsentsi (helendumine staatilises elektriväljas),
triboluminestsentsi (helendumine mehaaniliste
deformatsioonide toimel),
termoluminestsentsi
jms.
|
|
|
Üks universaalsemaid luminofoore on tsinksulfiid (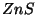 ). See
lihtne ja suhteliselt odav aine helendub pea kõigi võimalike
mõjutuste tagajärjel. Pisut häirib tema ebameeldivalt
sinakas toon, mida viimasel ajal edukalt "muudetakse
meeldivamaks", segades temasse noidsamu fluorestseeruvaid värve.
Tsinksulfiid on asendamatu röntgen- ja ultraviolettkiirte
muundaja, ta töötab nii teleekraanil, päevavalguslampides kui
radioaktiivse kiirguse indikaatorites. ). See
lihtne ja suhteliselt odav aine helendub pea kõigi võimalike
mõjutuste tagajärjel. Pisut häirib tema ebameeldivalt
sinakas toon, mida viimasel ajal edukalt "muudetakse
meeldivamaks", segades temasse noidsamu fluorestseeruvaid värve.
Tsinksulfiid on asendamatu röntgen- ja ultraviolettkiirte
muundaja, ta töötab nii teleekraanil, päevavalguslampides kui
radioaktiivse kiirguse indikaatorites.
Energeetilisest seisukohast toimub luminestsentsi korral keha
siseenergia muundumine valguseks. Siseenergia tüüp pole
siin oluline, niisamuti kui selle allikad.
|
|
|
Soojuslik ehk tasakaaluline kiirgus. Kui mingi keha asub kindla
temperatuuriga keskkonnas, nõuab termodünaamika teine printsiip,
et tema temperatuur peab tasakaaluoleku korral olema võrdne ümbritseva
keskkonna temperatuuriga.
Termodünaamika kursuses me ei
täpsustanud, mis teel toimub energia ülekanne kuumemalt kehalt
külmemale. Koolikursusest teame, et soojusülekanne toimub
soojusjuhtivuse, konvektsiooni või kiirguse teel. Kaks
esimest nõuavad juhtiva/ülekandva keskkonna olemasolu,
kolmas on universaalne.
|
Kiirgust, mida keha kiirgab termidünaamilise tasakaalu tingimustes (kindlal temperatuuril), nimetatakse tasakaaluliseks kiirguseks.
|
|
Soojusülekanne kiirgusega toimub sel teel, et kuumem keha
kiirgab rohkem energiat, kui neelab; külmem aga vastupidi -
neelab rohkem, kui kiirgab. Seetõttu esimese siseenergia väheneb
(temperatuur langeb), teise oma aga suureneb (temperatuur
kasvab).
Et kehadel pole aimugi teiste kehade (kiirgusallikate)
olemasolust, peab vaadeldav keha (aine) olema
termodünaamilises tasakaalus teda ümbritseva kiirgusväljaga.
Seda keha enda ja teiste kehade poolt tekitatud välja
iseloomustab kindel temperatuur; kiirgustasakaalu korral on see
võrdne vaadeldava keha temperatuuriga.
Viimane väide on õige vaid
isotroopse, st kõigist suundadest ühtlaselt tuleva kiirguse
jaoks. Kui keha valgustab mingi kindel allikas (näiteks Päike),
ei tähenda neelatud ja kiiratud energiate võrdsus veel saabuva
ja lahkuva kiirguse ühesugust temperatuuri.
|
|
|
Kiirgusvõime ja neelamisvõime.
Niisiis ei pea tasakaaluolekus olema võrdsed mitte
temperatuurid, vaid kiiratud ja neelatud energia kogused. Seetõttu
sõltub keha poolt kiiratud energia lisaks temperatuurile veel
tema kiirgusvõimest.
Et soojuskiirgus on elektromagnetlainetus,
sõltub kiiratud energia peale temperatuuri veel lainepikkusest
või sagedusest. Suurust 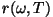 , mis väljendab keha
pinnaühikult ( , mis väljendab keha
pinnaühikult (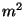 ) sagedusühiku ( ) sagedusühiku (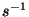 ) kohta kiiratud
energiat (dzaulides), nim. keha kiirgamisvõimeks. ) kohta kiiratud
energiat (dzaulides), nim. keha kiirgamisvõimeks.
|
Keha kiirgamisvõime näitab, kui palju energiat kaotab keha kiirguse tõttu.
|
|
Kui integreerida kiirgamisvõimet üle kõigi sageduste, saame suuruse
mida nimetatakse keha
kogukiirgusvõimeks e. valgsuseks.
Kui integreerime veel üle keha
pinna (eeldades, et kiirgusvõime on kõikjal ühesugune), saame
keha kogukiirguse; jagades selle 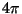 -ga aga vaadeldava
keha poolt ühikulisse ruuminurka kiiratava energiavoo. -ga aga vaadeldava
keha poolt ühikulisse ruuminurka kiiratava energiavoo.
Kui soovime leida valgustatud kehale juurde tulevat energiahulka, peame jagama valgustatud eseme
ristlõikepindala valgusallika kauguse ruuduga (milleks?) ning
arvestame tema neelamisvõimet.
|
|
Neelamisvõime on suurus,
mis väljendab "alla neelatud" energiahulga suhet kehale
langevasse energiasse. Kui tähistada mingile pinnatükile
langenud energiat 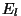 ning sellelt hajunud/peegeldunud
energiat ning sellelt hajunud/peegeldunud
energiat 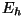 , saame selle pinnatüki koguneelamisvõimeks , saame selle pinnatüki koguneelamisvõimeks
|
Keha neelamisvõime näitab, kui suur osa kehale langevast kiirgusest neeldub, muutudes keha siseenergiaks.
|
Seegi suurus sõltub sagedusest ja temperatuurist, nii on
siingi otstarbekas defineerida neelamisvõime sagedusühiku kohta
antud temperatuuril:
|
|
|
Kirchoff'i seadus ja "must keha". Igapäevaelust teame,
et erinevate kehade neelamisvõimed on väga erinevad.
Kiirgamisvõime kohta me seda nii kindlalt väita ei saa - teame
küll, et keha kiirgab seda rohkem, mida kõrgem on tema temperatuur. rohkem.
Seda,
kuidas kiirgavad erinevad kehad ühl ja samal temperatuuril,
niisama lihtsalt ei ütle. Kui aga mõõtma hakata, tuleb välja
huvitav seos: tumedad kehad, mille neelamisvõime on suurem, kiirgavad
kuumutamisel tugevamini, kui heledad kehad.
Termodümaamika II printsiip seletab asja ära:
kui kiirgust
tugevasti neelav keha kiirgaks vähem, kui halvasti neelav keha
samal temperatuuril, hakkaks tema temperatuur tõusma teise keha
kiirguse arvel. Kui oletada, et algtemperatuur oli mõlemal kehal
võrdne, siis tuleks välja, et kiirgusliku energiavahetuse tõttu
võib tekkida temperatuuride erinevus. Aga selleks peab soojus
iseenesest minema üle külmemalt kehalt kuumemale, mis on
termodünaamiliselt võimatu.
Vastava seaduse formuleeris G.
Kirchoff 1859. a.
|
NB! ärge ajage segi Kirchoff'i reegleid (käivad hargnevate vooluahelate kohta) ja Kirchoff'i seadust (keha soojuskiirguse kohta). Mees on küll sama, aga teemad on erinevad.
Kui keha neelab kogu temale langeva kiirguse (neelamisvõime 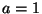 ) nimetatakse teda absoluutselt mustaks kehaks . ) nimetatakse teda absoluutselt mustaks kehaks .
|
|
Kiirgamisvõime ja neelamisvõime suhe on kõigil kehadel
sama, keha ja tema pinna omadustest sõltumatu funktsioon, mis
sõltub ainult temperatuurist ja sagedusest.
Funktsiooni
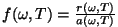 nimetatakse tavaliselt musta keha kiirgusvõimeks, kuna
"kõige tumedamal" ehk "absoluutselt mustal" kehal peab
neelamisvõime olema
nimetatakse tavaliselt musta keha kiirgusvõimeks, kuna
"kõige tumedamal" ehk "absoluutselt mustal" kehal peab
neelamisvõime olema 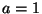 - ta neelab kogu pealelangeva
kiirguse. Et sellisel juhul - ta neelab kogu pealelangeva
kiirguse. Et sellisel juhul 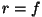 , tähendabki meie funktsioon
absoluutselt musta keha kiirgusvõimet. , tähendabki meie funktsioon
absoluutselt musta keha kiirgusvõimet.
Must keha on järjekordne matemaatilist laadi abstraktsioon; reaalsed kehad on "hallid" (neelamisvõime on ühest väiksem ja ei sõltu sagedusest) või "värvilised" (erinevatel sagedustel on neelamisvõime erinev).
Eksperimentaaloptikas kasutatakse "musta keha mudelit", kus õõnsa kera seina on puuritud auk. Sellesse auku langev valgus hajub kera sisepinnal ja tema kaudu väljuv osa kiirgusest on võrdne augu pinna ja kera kogupinna suhte ning sisepinna peegeldumisvõime (albeedo) korrutisega. Kui teha kera hästi suur ning auk väike, võime saada kuitahes suure (ühe-lähedase!) neeldumisvõime.
|
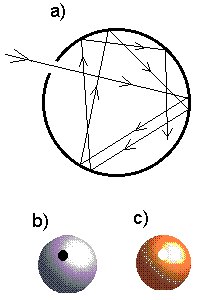
Musta keha mudel - auguga kera.
- kiirte käik õõnsuses;
- külmas keras paistab auk tumedana;
- kuumutatud kera pinnal on auk kõige heledam.
|
|
Küsimus: Mis juhtub, kui sellist kera kuumutada? Kumb paistab heledam, kas kera pind või selles olev auk? Ja miks?
Musta keha spekter ja kiirgusseadused. Funktsiooni
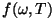 fundamentaalne iseloom kutsus esile vajaduse selle leidmiseks. "Ostsillaatoriteooriast"
lähtudes leidis W. Wien, et jaotusfunktsioon peab omama kuju fundamentaalne iseloom kutsus esile vajaduse selle leidmiseks. "Ostsillaatoriteooriast"
lähtudes leidis W. Wien, et jaotusfunktsioon peab omama kuju
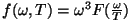 . .
Mõõtmised andsid
tulemuseks Maxwelli jaotust meenutava kõvera; mille kohta leidis Wien 1893. a. ka empiirilise valemi:
kus konstandid 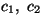 leitakse eksperimentaalselt.
Wieni
seadus kirjeldab spektri käiku rahuldavalt ning määrab õigesti
maksimumi asukoha. Viimase sõltuvust temperatuurist kirjeldab
märksa enam tuntud Wieni nihke seadus: leitakse eksperimentaalselt.
Wieni
seadus kirjeldab spektri käiku rahuldavalt ning määrab õigesti
maksimumi asukoha. Viimase sõltuvust temperatuurist kirjeldab
märksa enam tuntud Wieni nihke seadus:
|
Funktsiooni 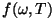 nimetatakse musta keha spektriks. nimetatakse musta keha spektriks.
NB! Spekter (ld spectrum - nägemus) tähendab matemaatikas jaotusfunktsiooni, mis seab vaadeldavale parameetrile (antud juhul sagedusele või lainepikkusele) vastavusse vastavate objektide (näiteks ostsillaatorite) suhtelise hulga.
Optikas tähendab spekter tavaliselt kiirgusvõime sõltuvust sagedusest (või lainepikkusest).
|
suurust 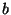 nim. Wieni konstandiks. nim. Wieni konstandiks.
Ka sobib seaduse
integreerimisel saadava Stefan-Boltzmanni seaduse
konstant piisavalt hästi eksperimendist leituga
(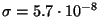 W W
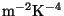 ). ).
|
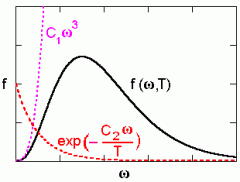
"Musta keha spekter" - Wien'i lähend.
Wien'i ja Stefan-Boltzmanni seadused on empiirilised , st saadud katsetulemuste matemaatilise üldistamise teel. Nende sidumine "ostsillaatoriteooriaga" viis kvantfüüsika tekkele.
|
|
"Ultravioletne katastroof". Kasutades möödunud sajandi
lõpus moes olnud statistilise mehaanika meetodeid, jõudsid
J. Rayleigh ja J. Jeans kaunis kahtlaste eelduste ning
keerulise matemaatika (vt. Saveljev III, lk. 194) abil valemini
mis küll rahuldab Wien'i tingimust, kuid annab täiesti
vastuvõtmatu tulemuse - kiirgusenergia piiramatu kasvu sageduse
suurenemisel. Et valem oli teoreetiliselt korrektne, hakati tema
vastuolu katsetulemusega nimetama ultravioletseks katastroofiks.
|
|
|
19. sajandi lõpp ongi klassikalise füüsika loojang. Kapitali
poolt loodud head uurimistingimused ülikoolides olid
genereerinud arvuka teadlaste klassi, kes aga kippus jätkama
vana, "filosoofilist", kõikeseletavat teadust.
Darvinism
bioloogias ning mehhanitsism füüsikas jätsid mulje "valmis
teadusest". Oli sündinud veel üks Megale Syntaxis -
Ptolemaiose ajast tuntud Suurim Ehitis, illusioon lõpetatud (või
peaaegu lõpetatud) tunnetusprotsessist.
Füüsikas jäid vaid kaks
"väikest pilvkest" - Michelsoni untsuläinud katse Maa kiiruse
määramiseks eetri suhtes ning "ultravioletne katastroof".
|
|
|
Planck'i valem. Aastal 1900 näitas saksa füüsik
M. Planck, et eksperimentaalset spektrit kirjeldab Wieni valemist
märksa täpsemini seos
mis on matemaatiliselt samaväärne Maxwelli jaotusega energiate
järgi eeldusel, et kiirgusvoog koosneb jagamatutest
energiakvantidest, mille energia on võrdeline sagedusega:
kus konstant
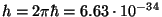 Js. Konstanti Js. Konstanti 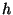 (
(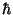 ) nimetamegi tänapäeval Planck'i konstandiks. ) nimetamegi tänapäeval Planck'i konstandiks.
|
Planck'i valem on saadud eeldusel, et ostsillaatori poolt kiiratav energiahulk on määratud kiiratava valguse sagedusega.
Tähelepanu: kaks fundamentaalkonstanti - gravitatsioonikonstant ja Planck'i konstant - on väga sarnaste tüvenumbritega.
Meeldejätmiseks:
väiksem on Planck -- 6.63,
suurem aga gravitatsioon -- 6.67.
|
|
Laine jagamine kvantideks on mehaanika seisukohalt võimatu.
Kui
ostsillaator kiirgabki piiratud aja vältel, tekib tema ümber
ikkagi vaid keralainete jada, mis meenutab kivi vette kukkumisel
veepinnale tekkivaid ringe. Et kiirata "lainepakett" kindlasse
suunda, on vaja keeruka ehitusega peegeldajat - näiteks võib
tuua prozektori paraboolpeegli.
Matemaatiliselt pole
sellega seni keegi maha saanud.
Ja kuidas mõista nüüd Huygensi
printsiipi?
Mis on lainefront ja kuidas tekib sekundaarlaine
solitoni ümber?
Kas ka see koosneb solitonidest?
Aga Planck'i valem töötab. Ja hüpotees kiirgusosakestest
võimaldab lahendada teisigi füüsika probleeme.
|
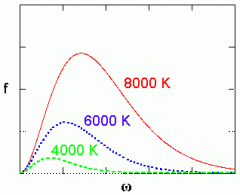
Planck'i spektrid kolmel erineval temperatuuril.
Kõvera alla jääv pindala on võrdeline temperatuuri neljanda astmega
|
|
Planck'i valemi tuletus (tõestus). Eeldused:
- Vibraatori energia sagedusel
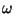 saab muutuda
vaid saab muutuda
vaid 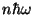 korda, kus korda, kus 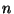 on täisarv. on täisarv.
- Vibraatori oleku tõenäosus sõltub tema energiast
vastavalt Boltzmanni valemile:
kus
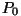 on põhiolekus on põhiolekus 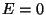 olevate vibraatorite arv. olevate vibraatorite arv.
- Antud sagedusel kiiratav energia on võrdne seda
sagedust omavate vibraatorite koguenergiaga.
|
Planck'i valemi tuletamisel kasutame lõpmatute ridade teooriat.
NB! See tuletus kuulub kohustuliku materjali hulka.
|
|
Arvutame vibraaatori keskmise energia:
Taandame 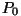 ning tähistame ning tähistame
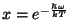 .
Kõik .
Kõik 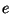 kõrgemad astmed asenduvad nüüd kõrgemad astmed asenduvad nüüd 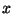 astmetega: astmetega:
Ja nüüd tuleb matemaatiline fookus. Arvutame avaldise:
mis lõpmatu rea korral võrdub lugejas oleva summaga 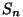 ! !
Edasi käib lihtne algebra. Võrdusest
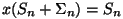 saame saame
Pannes selle Rayleigh'-Jeans'i valemisse asendamaks
ostsillaatori "termodünaamilist energiat" 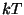 , saamegi Plancki valemi. , saamegi Plancki valemi.
|
|
|
Fotoefekti teooria. Footonid.Planck ise pidas oma valemit vaid
teravmeelseks arvutusvõtteks, mis ju väga vale polegi. Alles
A. Einsteini poolt 1905. a. leitud rakenduste seeria hakkas
viima mõtteid sellele, et kvant (lad. quantum - ports,
kogus) kui valguse osake võiks reaalselt eksisteerida. Einsteini
kiirgusülekande valemid kuuluvad pigem kvantmehaanika valdkonda,
seepärast praegu vaid ühest kõige efektsemast valemist.
|
Kvanthüpoteesi esimeseks rakenduseks ning ka kõige veenvamaks tõestuseks on Albert Einsteini poolt 1905.a. esitatud fotoefekti teooria.
|
|
Fotoefektiks nimetati elektronide väljumist metallist valguse
toimel. Uurijad märkasid, et mitte igasugune valgus ei mõju
antud metalli elektronidele, vaid alati on olemas kindel
maksimaalne lainepikkus (nn. fotoefekti punapiir), millest
pikematel lainetel valgus metallile enam ei mõju, olgu ta
kuitahes suure intensiivsusega.
Laineteooria seda seletada ei
suutnud - pidi ju energia pidev neeldumine lõpuks ikkagi mõne
elektroni vabastama. Punapiir oli eri metallidel erinev: kõige
väiksem tseesiumil ja teistel leelismetallidel, raual seevastu
kaugel röntgenikiirte piirkonnas.
|
Footon ehk "valguskvant" on aine (keskkonna) poolt kiiratav või neelatav minimaalne energiakogus, mis on võrdeline kiiratava valguslaine sagedusega.
|
|
Einstein seletas asja lihtsalt:
et aine koosneb aatomitest,
vabaneb elektron vaid siis, kui temale antav energia ületab
elektroni metalliga siduva jõu potentsiaalse energia.
Valemist
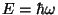 lähtudes saab seda teha vaid kiirgus, mille
kvandi energia (Plancki valemi järgi on see võrdeline
sagedusega) on suurem elektroni potentsiaalsest energiast.
Viimane on eri metallidel erinev ja seetõttu on erinev ka
piirsagedus. lähtudes saab seda teha vaid kiirgus, mille
kvandi energia (Plancki valemi järgi on see võrdeline
sagedusega) on suurem elektroni potentsiaalsest energiast.
Viimane on eri metallidel erinev ja seetõttu on erinev ka
piirsagedus.
Kui pealelangeva valguse sagedus on väiksem
(lainepikkus suurem) energiast 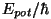 , vabu elektrone
ei teki. Kui energia on suurem, kehtib valem , vabu elektrone
ei teki. Kui energia on suurem, kehtib valem
See ongi Einsteini valem; konstant
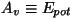 aga kannab
väljumistöö nime. aga kannab
väljumistöö nime.
|
|
|
Lihtne ja loogiline, nagu kõik noore Einsteini asjad. Ainult et
siin pole "kvant" enam arvutuslik vahend, vaid reaalne, mõõdetav
füüsikaline objekt. Talle anti ka nimi - footon. Valguse osake.
Aga mitte enam korpuskel! See on laine osake, midagi uut
inimtunnetuse jaoks. Oli sündinud esimene dualistlik (lad.
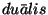 - kahene) füüsikaline objekt. - kahene) füüsikaline objekt.
|
Planck'i konstant 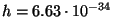 Js on sagedust kvandi energiaga siduv võrdetegur, üks looduse põhikonstante.
Js on sagedust kvandi energiaga siduv võrdetegur, üks looduse põhikonstante.
|
|
Bose versus Boltzmann. Tuleme veel kord Planck'i
valemi juurde. Tema põhiline erinevus Maxwelli jaotusega
võrreldes on eksponentliikme
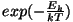 asendumine
suhtega asendumine
suhtega
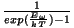 -ga. -ga.
Vastavalt saame ka kaks statistilist jaotust
Neist vasakpoolne käis aatomite-molekulide kohta, parempoolne
aga peaks kirjeldama footonite jaotust energiate järgi.
Hiljem,
kui kvantmehaanikat tehti, tuli välja, et Boltzmanni valem on
märksa fundamentaalsemate statistiliste jaotuste piirjuht. Üks
neist on meil käes - see on nn. Bose-Einsteini jaotus,
mis kvantmehaanikas kirjeldab mitteeristatavaid osakesi.
Teisest tuleb juttu järgmises peatükis.
Piirjuht tähendab aga seda, et kui 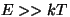 , on nimetajas olev
eksponent palju suurem talle liidetavast ühest. Jätame selle ära
ning saamegi Boltzmanni valemi. , on nimetajas olev
eksponent palju suurem talle liidetavast ühest. Jätame selle ära
ning saamegi Boltzmanni valemi.
|
Kaasaegne füüsika loeb footonit iseseisvaks (elementaar)osakeseks.
Elementaarosakeste teoorias tuletatakse Planck'i jaotus osakeste (antud juhul footonite) eristamatuse printsiibist.
Selliseid osakesi nimetatakse bosoniteks , vastavat jaotusfunktsiooni Bose-Einsteini jaotuseks.
|
![]() Valguse vastasmõju keskkonnaga
Valguse vastasmõju keskkonnaga
![]() Ostsillaatoritest koosnev keskkond
Ostsillaatoritest koosnev keskkond
![]() Valguse murdumine
Valguse murdumine
![]() Dispersioon
Dispersioon
![]() Neeldumine
Neeldumine
![]() Polarisatsioon
Polarisatsioon
![]() Polarisatsioon hajumisel
Polarisatsioon hajumisel
![]() Polarisatsioon peegeldumisel
Polarisatsioon peegeldumisel
![]() Polarisatsioon anisotroopses kristallis
Polarisatsioon anisotroopses kristallis
![]() Polarisatsioon neeldumisel
Polarisatsioon neeldumisel
![]() Polarisatsioon tehnikas
Polarisatsioon tehnikas
![]() Keskkond kiirgajana
Keskkond kiirgajana
![]() Luminestsents
Luminestsents
![]() Soojuslik ehk tasakaaluline kiirgus
Soojuslik ehk tasakaaluline kiirgus
![]() Kiirgusvõime ja neelamisvõime
Kiirgusvõime ja neelamisvõime
![]() Kirchoff'i seadus
Kirchoff'i seadus
![]() Musta keha spekter
Musta keha spekter
![]() Wien'i nihke seadus
Wien'i nihke seadus
![]() Stefan-Boltzmanni seadus
Stefan-Boltzmanni seadus
![]() "Ultravioletne katastroof"
"Ultravioletne katastroof"
![]() Planck'i valem
Planck'i valem
![]() Planck'i valemi tuletus (tõestus)
Planck'i valemi tuletus (tõestus)
![]() Fotoefekti teooria. Footonid
Fotoefekti teooria. Footonid
![]() Bose versus Boltzmann
Bose versus Boltzmann
![]()