Loeng 15. Sundvõnked ja vahelduvvool.
Liikumisvõrrand harmooniliselt muutuva jõu korral.
Olgu meil võnkumisvõimeline süsteem, mille liikumist kirjeldab diferentsiaalvõrrand
Nagu eelmises loengus leidsime, on selle võrrandi lahendiks eksponentsiaalselt kahaneva amplituudiga võnkumised
kus
(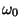 on sagedus, millega võnguks süsteem takistava jõu puudumisel. Et tegu on süsteemi olulise parameetriga, nimetame teda edaspidi süsteemi omasageduseks.) on sagedus, millega võnguks süsteem takistava jõu puudumisel. Et tegu on süsteemi olulise parameetriga, nimetame teda edaspidi süsteemi omasageduseks.)
|
Sundvõnked tekivad võnkumisvõimelises süsteemis harmooniliselt muutuva välisjõu toimel.
|
|
Vaatleme juhtu, kus sellele süsteemile
mõjub harmooniliselt muutuv jõud
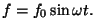 Süsteemi liikumist kirjeldab nüüd mittehomogeenne teist järku diferentsiaalvõrrand
Süsteemi liikumist kirjeldab nüüd mittehomogeenne teist järku diferentsiaalvõrrand
Muidugi on ka selliste võrrandite lahendamiseks terve teooria, meie katsume lihtsamalt läbi ajada.
|
Süsteemile mõjuvat välisjõudu nimetame sundivaks jõuks.
|
|
Sundvõnked.
Oletame, et süsteem hakkab võnkuma
sundiva jõu sagedusega ning selle võnkumise amplituudi 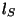 ja algfaasi ja algfaasi 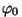 määravad sundiva jõu amplituud määravad sundiva jõu amplituud 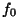 ning võnkuva süsteemi parameetrid: omasagedus ning võnkuva süsteemi parameetrid: omasagedus 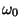 ja sumbuvustegur ja sumbuvustegur 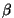
|
Süsteemi parameetriteks on omasagedus ja sumbuvustegur; need leitakse vabavõngete võrrandist sundiva jõu puudumisel.
|
Püüame leida konstandid 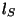 ja ja 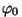 . Teeme seda
vanaviisi: võtame tuletised . Teeme seda
vanaviisi: võtame tuletised
saame
Grupeerime vasaku poole liikmeti:
Joonistame nüüd sellele vastava faasidiagrammi
ning kasutades Pythagorase teoreemi saame
millest leiame sundvõngete amplituudi
|
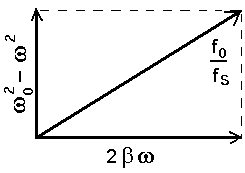
Sundvõngete faasidiagramm:
siinusfunktsiooni kordaja on y -teljel, koosinusliikme oma x -teljel. Et lahend vastaks lähtevõrrandile, peab nende summa olema võrdne sundiva jõuga.
|
Faasinihke 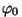 sundiva jõu sundiva jõu 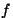 suhtes leiame
tangensist suhtes leiame
tangensist
Näeme, et nii faasinihe kui amplituud sõltuvad
sundiva jõu sageduse ning süsteemi omasageduse vahest. Kui see
on null, on faasinihe 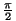 ning amplituud maksimaalne: ning amplituud maksimaalne:
Väikese sumbuvusteguri 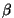 korral võib korral võib 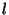 omandada
küllalt suure väärtuse. Seda olekut nimetatakse
resonantsiks. omandada
küllalt suure väärtuse. Seda olekut nimetatakse
resonantsiks.
Elektrilised sundvõnked. Vaatleme vooluringi, kus harmooniliselt muutuva elektromotoorjõu allikaga on jadamisi ühendatud kondensaator, induktiivpool ja tavaline (oomiline) takisti. Kui vooluallikat poleks, oleks tegu eelmises loengus käsitletud võnkeringiga. Kirjutame selle ahela võrrandi, lähtudes Kirchoffi II reeglist:
ehk
Asendades voolutugevuse
 ning jagades võrrandi mõlemaid pooli ning jagades võrrandi mõlemaid pooli 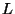 -ga, saame võrrandi -ga, saame võrrandi
|
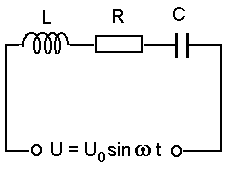
Vahelduvvooluring.
|
mis on matemaatiliselt identne eespool toodud sundvõnkumiste võrrandiga.
Selle lahendiks on (analoogselt eelnevaga):
Võrrand kirjeldab kondensaatoril oleva laengu muutumist meie poolt uuritavas võnkeringis harmooniliselt muutuva elektromotoorjõu mõjul.
|
|
|
Vahelduvvool. Nii tööstus kui olmetehnika kasutavad valdavalt vahelduvvoolu, mis tekib magnetväljas pöörlevas mähises genereeritava induktsiooni elektromotoorjõu mõjul. Kui generaator töötab stabiilse kiirusega, muutub tekkiv elektromotoorjõud võrdeliselt pöördenurga siinusega, seega harmoonilise võnkumise seaduse kohaselt.
|
Vooluringis kulgevat vahelduvvoolu võib matemaatiliselt käsitleda kui elektrilisi sundvõnkumisi.
|
|
On loogiline oletada, et harmooniliselt võngub ka voolutugevus. Meie poolt leitud "laengu võnkumise valem" näib seda kinnitavat. Et voolutugevus on defineeritud kui laengu tuletis aja järgi, võtame saadud valemist tuletise:
Suurust 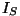 võime vaadelda kui voolutugevuse amplituudväärtust. Nagu näeme, on ta võrdeline pinge (elektromotoorjõu?) amplituudväärtusega võime vaadelda kui voolutugevuse amplituudväärtust. Nagu näeme, on ta võrdeline pinge (elektromotoorjõu?) amplituudväärtusega 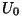 : :
Leitud valemites olevatel suurustel on vahelduvvoolu teoorias ka kindlad nimed:
-
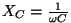 mahtuvuslik takistus, mahtuvuslik takistus,
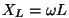 - induktiivtakistus, - induktiivtakistus,
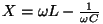 - reaktiivtakistus, - reaktiivtakistus,
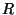 - aktiivtakistus, - aktiivtakistus,
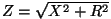 kogutakistus kogutakistus
|
Vahelduvvooluahela takistus jaguneb aktiiv- ja reaktiivtakistuseks; viimane koosneb induktiiv- ja mahtuvuslikust takistusest.
|
|
Kui kirjutada meie valemid ümber neid tähiseid kasutades, saame Ohm'i seaduse üsna tuttaval kujul
Võime leida ka pinged (pingelangud) ahela üksikutel komponentidel:
- Kondensaator ("mahtuvuslik takistus"):
- Induktiivsus ("induktiivtakistus"):
Need kaks pingelangu on alati vastasfaasis (st. vastasmärgilised!)
Pingelang takistil (aktiiv- ehk oomiline takistus) tuleb nagu alalisvoolugi korral:
|
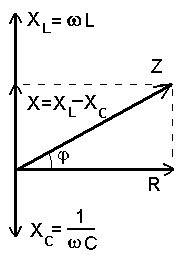
Kogutakistus faasidiagrammil.
Pingelangud induktiiv- ja mahtuvuslikul takistusel on vastasfaasis.
|
|
Vahelduvvoolu faasidiagramm. Kui võtsime laengust tuletise, jätsime tähelepanuta asjaolu, et tuletise võtmisel muutus faasiliikme siinus koosinuseks. Ega sellest midagi pole, harmooniliste võnkumiste kirjeldamiseks sobivad mõlemad funktsioonid. Küll aga tuleb meil seda arvestada faasidiagrammi joonistamisel.
Elektrimeestel on siin omad traditsioonid, mida tasub järgida. Vahelduvvoolu faasidiagrammidel on voolutelg (pingelang oomilisel takistusel) tavaliselt rõhtsuunas (x-telje kohal).
Kuna vooluvektori projektsioon x-teljele avaldub koosinuse kaudu, eelistatakse valemites koosinust siinusele.
Trigonomeetriast teame, et
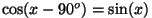 ja ja
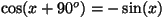 .
Võrdeliselt .
Võrdeliselt 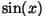 -ga muutus meie võnkeringis laeng (siis ka pinge!) kondensaatoril, temaga vastasfaasis
( -ga muutus meie võnkeringis laeng (siis ka pinge!) kondensaatoril, temaga vastasfaasis
(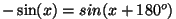 ) aga induktsiooni elektromotoorjõud - pinge induktiivpoolil. ) aga induktsiooni elektromotoorjõud - pinge induktiivpoolil.
Nii ongi meie faasidiagrammil vooluvektor suunatud paremale, pingelang kondensaatoril alla ja pingelang induktiivsusel üles.
See, kuhu satub summaarne vektor U, sõltub mahtuvusliku ja induktiivtakistuse vahekorrast:
kui need on võrdsed (resonantsolukord), on vektorid U ja IR samasuunalised ning faasinihe 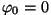 .
kui mitte, siis kas positiivne ( .
kui mitte, siis kas positiivne (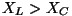 ) või negatiivne ( ) või negatiivne (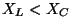 ). ).
|
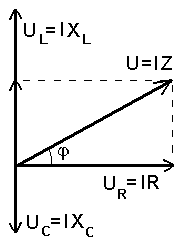
Vahelduvoolu faasidiagramm.
Joonisel on induktiivtakistus mahtuvuslikust takistusest suurem ja faasinihe positiivne.
|
|
Resonantsid. Jadalülituse korral kehtib ülaltoodud
valem:
kus
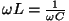 vastab
Zmin , Imax.
Seega on resonantsolukorras ahela takistus minimaalne ning
voolutugevus maksimaalne. Elektrotehnikas nimetatakse seda olukorda pingeresonantsiks. vastab
Zmin , Imax.
Seega on resonantsolukorras ahela takistus minimaalne ning
voolutugevus maksimaalne. Elektrotehnikas nimetatakse seda olukorda pingeresonantsiks.
Vaatame nüüd sellist
vahelduvvooluahela elementi, kus induktiivsus ja mahtuvus on
lülitatud paralleelselt.
Takistuste rööplülituse valemi
järgi kehtib
|
Pingeresonants tekib jadalülituse, vooluresonants rööplülituse korral. Miks neid nii nimetatakse, küsige elektrimeestelt.
|
Näeme, et
See, et ahela takistus
kasvab lõpmata suureks, tähendab voolu lakkamist. Elektrotehnikas nimetatakse sellist olukorda nim. vooluresonantsiks. Füüsikaliselt võime kujutleda, et vahelduvpinge ahela
lahknemispunktis  genereerib paralleelharudes
vastasfaasis olevad elektrivõnked, mistõttu punkti genereerib paralleelharudes
vastasfaasis olevad elektrivõnked, mistõttu punkti  potentsiaal saab nulliks.
potentsiaal saab nulliks.
Loomulikult pole tegelik takistus ei null ega lõpmatus. Igas ahelas on
alati olemas ka oomiline e. aktiivtakistus 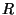 , mis muudab kogutakistuse nullist erinevaks. Vaadake faasidiagrammi:
resonantsolukorras võrdub kogutakistus , mis muudab kogutakistuse nullist erinevaks. Vaadake faasidiagrammi:
resonantsolukorras võrdub kogutakistus 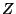 alati oomilise takistusega alati oomilise takistusega
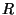 . .
Täpne resonantssagedus. Oomilise takistuse korral erineb
vabavõngete sagedus 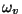 omasagedusest omasagedusest 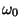 . Resonantsitingimuses lähtusime seni omasagedusest,
põhjendades seda liikme . Resonantsitingimuses lähtusime seni omasagedusest,
põhjendades seda liikme
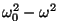 minimaalväärtusega
kogutakistuse valemis. minimaalväärtusega
kogutakistuse valemis.
Tegelikult oleneb juurealuse avaldise
väärtus mõlemast liikmest - kui esimese lähenemisel nullile
muutub teine kiiremini, nihkub ka kogu avaldise miinimum
nullpunktilt kõrvale.
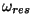 täpse väärtuse saame
ekstreemumtingimusest täpse väärtuse saame
ekstreemumtingimusest
Võttes lugejast tuletise ning võrrutades selle nulliga, saame:
|
|
ehk
Näeme, et funktsioonil on kaks ekstreemumit:
|
Sagedust, mille korral kogutakistus on minimaalne, nimetatakse resonantssageduseks.
|
Esimene neist tähendab harmooniliselt muutuva välisjõu puudumist, teisest saame
Seega on täpne resonantssagedus
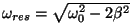 - mõnevõrra väiksem vabavõngete sagedusest
- mõnevõrra väiksem vabavõngete sagedusest
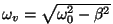 . .
|
|
|
Võimsus vahelduvvooluahelas. Et vahelduvvool kõigele
vaatamata teeb ka tööd, tuleks leida valem selle töö -
täpsemalt küll võimsuse - hindamiseks. Tavaline Joule-Lenz'i
valem meid ei rahulda, kuna ei arvesta reaktiivvõimsustel
(näiteks mootor või trafo) tehtavat tööd.
Et leida võimsust,
peame ahelale rakendatud elektromotoorjõu (võrgupinge) korrutama
voolutugevusega, arvestades faasinihet:
|
Vahelduvvooluahela võimsus sõltub lisaks pingele ja voolutugevusele ka faasinihkest.
|
Rakendades trigonomeetriast summa siinuse valemit, saame
Saime ajas muutuva suuruse, mis väljendab hetkvõimsust
ajamomendil 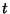 ja millega pole suurt peale hakata.
Keskmise
võimsuse leidmiseks integreerime saadud avaldist ühe perioodi
vältel ning jagame siis perioodi väärtusega: ja millega pole suurt peale hakata.
Keskmise
võimsuse leidmiseks integreerime saadud avaldist ühe perioodi
vältel ning jagame siis perioodi väärtusega:
Teine integraal on vastavalt perioodi definitsioonile
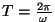 võrdne nulliga. Esimesest saame: võrdne nulliga. Esimesest saame:
kuna
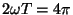 , millest siinus annab jällegi nulli. , millest siinus annab jällegi nulli.
Seega erineb vahelduvvooluahela keskmine võimsus alalisvoolu
ahela omast teguri 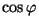 võrra. Seda faasinihkest
sõltuvat tegurit nimetataksegi võimsusteguriks. Võimsus on
seega maksimaalne, kui faasinihe on null. võrra. Seda faasinihkest
sõltuvat tegurit nimetataksegi võimsusteguriks. Võimsus on
seega maksimaalne, kui faasinihe on null.
|
Võimsuse valemisse kuuluvat kordajat 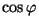 nimetatakse ahela võimsusteguriks. nimetatakse ahela võimsusteguriks.
|
|
Efektiivväärtused. Faasinihe tuleb sisse vaid siis,
kui ahelas on nullist erinev reaktiivtakistus. Kui asi piirdub
oomilise takistusega 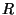 , on , on 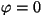 , , 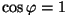 ning ning
Vahelduvvoolu efektiivväärtused defineeritakse kui
aktiivtakistusel sama võimsuse tekitava alalisvoolu (-pinge)
väärtused. Tegur 1/2 jagatakse nende vahel võrdselt, saades
NB! Meile harjumuspärased 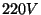 ja ja 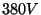 on nimelt
efektiivväärtused.
Lisaks efektiivväärtustele võime leida ka vahelduvoolu keskväärtuse: on nimelt
efektiivväärtused.
Lisaks efektiivväärtustele võime leida ka vahelduvoolu keskväärtuse:
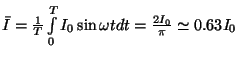 . .
Küsimus: Aga vahelduvpinge keskväärtus?
|
Vahelduvvoolu pinget ja voolutugevust võib esitada nii maksimaalväärtuse (amplituudi) kui efektiivväärtuse kaudu.
Efektiivväärtused defineeritakse sama võimsusega alalisvoolu abil. Nad erinevad pinge ja voolutugevuse keskväärtustest.
Tehnilises dokumentatsioonis antavad pinge ja voolutugevus on reeglina efektiivväärtused.
|
|
Tasub meeles pidada trigonomeetriliste funktsioonide keskväärtusi:
|
|
|
Kvaasistatsionaarsuse nõue. Kui võnkesagedus on väga suur, muutub oluliseks ka potentsiaali hilinemine. Nii nimetatakse elektroonikas aega, mis kulub elektrilisel signaalil jõudmiseks ahela ühest punktist teise. Et elektriväli levib juhtmetes praktiliselt valguse kiirusega, on normaalmõõtmetega ahelates see hilinemine väike.
Aga kui väike? Võttes sageduseks Euroopa võrgustandardi 50 Hz, saame näiteks kilomeetri pikkuse juhtme kohta hilinemise 1/300000 sekundit. See annab faasinihke juhtme otste vahel
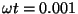 radiaani ehk 3.6 kaareminutit. Sellele vastav siinuse viga oleks 0.2%. radiaani ehk 3.6 kaareminutit. Sellele vastav siinuse viga oleks 0.2%.
Kui aga arvutada faasinihet raadiosaatjas või arvutiskeemis taktsagedusel 100 MHz, muutub hilinemine oluliseks. Sellisel juhul meie valemid ei kehti ning tuleb lähtuda lainefüüsikast.
Inseneriarvutustes kasutatakse omamoodi "kirvereeglit", mida nimetatakse kvaasistatsionaarsuse ("peaaegu statsionaarne") nõudeks. Vahelduvvooluringi tohib rehkendada siintoodud valemitega vaid juhul, kui
aeg, mis kulub signaalil vooluringi läbimiseks, on alla sajandiku võnkeperioodist.
Valemina:
|
Vahelduvvoolu, mille puhul voolutugevuse faasi võib ahela kõigis punktides lugeda samaks, nimetatakse kvaasistatsionaarseks.
|
c = 300000 km/s on valguse kiirus.
Kompleksarvude meetod. Elektrotehnikas kasutatakse vahelduvvoolu rehkendamisel sageli kompleksarve. Sellel on kaks põhjust.
- Kompleksarvude abil saab esitada võnkumisi eksponentfunktsiooniga, mille integreerimine-diferentseerimine on märksa lihtsam kui trigonomeetriliste funktsioonide korral.
- Kompleksarvu geomeetriline kuju vastab täpselt faasivektori ideoloogiale võnkumiste liitmisel
|
|
Alustame viimasest. Kujutame näiteks voolutugevust kompleksarvuga (et kompleksarvu tavalisest eristada, paneme vastavale sümbolile "katuse" peale)
Nagu matemaatikas õpitud, saab kompleksarve anda ka nn. trigonomeetrilises kujus:
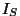 on kompleksarvu moodul, on kompleksarvu moodul, 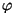 aga argument.
Kui argument on võrdeline ajaga, saamegi komplekstasandil pöörleva vektori aga argument.
Kui argument on võrdeline ajaga, saamegi komplekstasandil pöörleva vektori 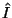 , mille reaal- ja imaginaarosa muutuvad harmoonilise võnkumise võrrandi kohaselt. , mille reaal- ja imaginaarosa muutuvad harmoonilise võnkumise võrrandi kohaselt.
Et kirjapilti veelgi lihtsamaks teha, teisendame meie kompleks-voolu eksponentfunktsiooniks, kasutades Euleri valemeid (vt. lisatekst)
ning asendame
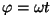 , saades , saades
|
Arvutuste lihtsustamiseks võib võib vahelduvvoolu pinget ja voolutugevust esitada kompleksarvudega.
Euleri valem (vt. lisateksti) lubab kompleksarve esitada eksponentfunktsiooni kujul.
|
Kui võtta sellest tuletis ja korrutada induktiivsusega, saame pingelangu induktiivpoolil:
Pinge kondensaatoril leiame, jagades laengu mahtuvusega. Et laeng on voolutugevuse integraal (tuletise pöördtehe!), saame
Miks on 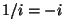 ? Mõelge ise välja! ? Mõelge ise välja!
Vihje: tuletage meelde, kuidas defineeritakse imaginaarühik.
Pingelang takistil on loomulikult "tavaline"
Ja nüüd võtame nad kõik kokku Kirchoff'i reegliks:
|
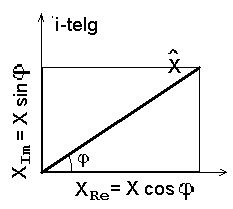
Kompleksarvu trigonomeetriline kuju on samaväärne faasidiagrammiga (phasor'iga).
|
Kui tuua 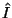 sulgude ette, saamegi Ohm'i seaduse vahelduvvooluahela jaoks: sulgude ette, saamegi Ohm'i seaduse vahelduvvooluahela jaoks:
kus
kannab nime komplekstakistus.
Kuidas selle põhjal teha faasidiagrammi, katsuge ise välja mõelda. Kui valmis, võrrelge ülaltoodutega.
Kasutades kompleks-sümboolikat, võime vahelduvvooluahelaid rehkendada alalisvoolu valemitega.
Küsimus: Kas oskate sama metoodikat kasutada näiteks harmooniliste võnkumiste liitmisel?
|
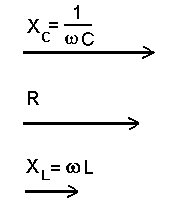
Komplekstakistus faasidiagrammil.
Vektor Z (katusega) joonistage ise.
|
![]() Sundvõnked
Sundvõnked
![]() Elektrilised sundvõnked
Elektrilised sundvõnked
![]() Vahelduvvool
Vahelduvvool
![]() Vahelduvvoolu faasidiagramm
Vahelduvvoolu faasidiagramm
![]() Resonantsid
Resonantsid
![]() Täpne resonantssagedus
Täpne resonantssagedus
![]() Võimsus vahelduvvooluahelas
Võimsus vahelduvvooluahelas
![]() Efektiivväärtused
Efektiivväärtused
![]() Kvaasistatsionaarsuse nõue
Kvaasistatsionaarsuse nõue
![]() Kompleksarvude meetod
Kompleksarvude meetod
![]()