Loeng 17. Valgus: geomeetriline optika ja fotomeetria
Optika.
Nimetus optika tuleneb kreeka keelest, kus
"optike" tähendab nägemist, nägemisvõimet. Sõna tõi tema
praeguses tähenduses teadusse Newton, kes pealkirjastas nii oma 1704. a. ilmunud töö
"Optika ehk traktaat valguse peegeldumisest, murdumisest,
kõverdumisest ja värvidest" (Optics or a treatise of the
reflections, refractions, inflections and colours of light). Igapäevaelus tähistab sõna "optics" Inglismaal
prillipoodi.
Niisiis: teadus valguse levimisest. Sõna "valgus" vajaks
füüsikas samuti täpsustamist. Praegu mõistame me (enda arvates?)
selle all elektromagnetlaineid lainepikkuste vahemikus umbes
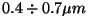 . .
|
Optika on valgusõpetus.
Valguse all mõistame silmaga nähtavat elektromagnetkiirugust.
|
|
Aga ega see pole ka mingi füüsika. Mida
tähendab "ligikaudu"? Ja mis "elektromagnetlaine" - see pole ju
nähtus, vaid kirjeldus! Ütleks, et "silmaga nähtavad
elektromagnetlained" - aga kõik optika seadused kehtivad ka
"mittenähtavate" infrapunaste ja ultraviolettkiirte kohta.
Objektiivselt võttes ongi tänapäeva optika elektromagnetlainete
levimist käsitlev füüsikaharu; nägemisega teda eriti ei
seostata. Tehnikas, kus on vaja arvestada valguse mõju
inimsilmale, oleme sunnitud kasutama fotomeetrilisi
suurusi ja see ongi peaaegu et ainus koht, kus nägemine (
optike) sisse tuleb.
|
Laiemas mõttes mõistame optika all elektromagnetlainete tekke ja levikuga tegelevat füüsikaharu.
|
|
Natuke annab mõistele "valgus" selgust
teda tähistavate sõnade kõrvaltähendus erinevates keeltes.
Eestlased on oma termini saanud ilmselt valgest värvist,
arvestades meie kuulumist germaani kultuuriareaali on see üsna
sarnane sakslastele ("licht" omadussõnana tähendab "hele",
"hõre"). Inglaste "light" vastab omadussõnale "kerge" ja
kõige ilmekam on vast venelaste "svet" - samaaegselt nii
"valgus" kui "maailm".
Et inimese välistaju põhineb 90% ulatuses nägemismeelel, on ka
meie maailmapilt "optilis-ruumiline". See, nagu taolistel
juhtudel tavaline, raskendab valguse kui "pilditekitaja"
mõistmist. Tavaliselt kasutame terminit valguskiir,
mõistes selle all silmast või valgusallikast lähtuvat ning
vaatluse all oleva objektiga lõppevat sirglõiku. Mida see kiir
endast kujutab, on kaunis raske seletada. Tõsi küll, mõnikord
on ta isegi nähtav - tolmuses või suitsuses ruumis näiteks.
Newton, harjunud tema ajal moes olevate postulatiivsete
süsteemidega, tõi välja neli optika põhiseadust:
|
Valgusõpetus tugineb Newtoni poolt formuleeritud neljale põhiseadusele.
|
- Valgus levib sirgjooneliselt.
- Valguskiired on sõltumatud: iga kiir levib ruumis nii,
nagu poleks teisi olemas.
- Valguse peegeldumisel tasaselt pinnalt on langev kiir,
peegeldunud kiir ja langemispunkti tõmmatud pinnanormaal ühes
tasandis. Langemisnurk võrdub peegeldumisnurgaga.
- Valguse üleminekul ühest keskkonnast teise kiir murdub
(muudab suunda), kusjuures langev kiir, murdunud kiir ja
langemispunkti tõmmatud pinnanormaal on ühes tasandis.
Langemisnurga ja murdumisnurga siinuste suhe on antud
keskkondade paari jaoks konstantne suurus ega sõltu
langemisnurgast.
|
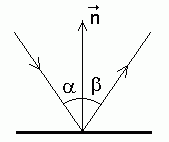
Valguse peegeldumine:
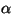 on langemisnurk, on langemisnurk, 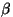 peegeldumisnurk, peegeldumisnurk, 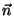 peegeldavale pinnale tõmmatud normaal (ristsirge).
peegeldavale pinnale tõmmatud normaal (ristsirge).
|
Pea meeles:
- Langemis-, peegeldumis- ja murdumisnurkade all mõistetakse
kiirte ja pinnanormaali vahelisi nurki.
- Siinuste suhtega
võrduv konstant
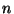 kannab nimetust suhteline
murdumisnäitaja e. teise keskkonna (kuhu valgus jõuab hiljem)
murdumisnäitaja esimese keskkonna suhtes. kannab nimetust suhteline
murdumisnäitaja e. teise keskkonna (kuhu valgus jõuab hiljem)
murdumisnäitaja esimese keskkonna suhtes.
- Ainete murdumisnäitajaid
vaakumi (tühjuse!) suhtes nimetatakse absoluutseteks.
Lihtne matemaatika näitab, et suhteline murdumisnäitaja on
absoluutsete murdumisnäitajate suhe:
|
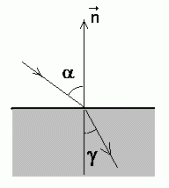
Murdumisseadus. 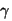 on murdumisnurk. on murdumisnurk.
|
|
Vaatame pilti, kus ainete 1 ja 2 vahel on vaakum. Kiire teel
esimesest keskkonnast teise tuleb ette kaks murdumist, kusjuures
murdumisseaduse järgi
Korrutades need võrdused omavahel ja arvestades,
et
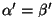 , saame , saame
|
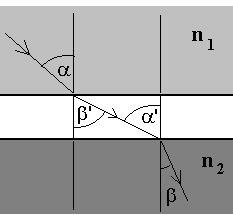
Absoluutne ja suhteline murdumisnäitaja.
"Vaakumist vahekihi" läbimisel on murdumisnurk 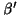 võrdne langemisnurgaga teise keskonna piiril võrdne langemisnurgaga teise keskonna piiril 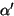 . .
|
|
17. saj. lõpuks olid loetletud seadused hästi teada, vast teine
seadus välja arvatud. Kiirte sõltumatus pole iseenesest vajalik,
tema ületähtsustamine on tingitud Newtoni mehhanistlikust
maailmapildist. Oli ju seni õnnestunud kõiki nähtusi kirjeldada
kehade liikumisega - miks siis mitte ka valgust. Kui valguskiir
oleks kehade voog, tuleks kiirte sõltumatust eraldi vaadelda,
sest "põrkuvad kiired" peaks tekitama hajumise, mida
tegelikkuses ei täheldata.
Ajaloost. Ajaloolises plaanis on valgusnähtuste uurimine vast üks kõige dramaatilisema arenguga füüsikavaldkondi. Juba põhikontseptsiooni areng (vaheldumisi kord laine, kord osake) näitab, et tegu on tavaterminites raskesti kirjeldatava objektiga. Et valguse puudumisel kaotab inimene suurema osa oma orienteerumisvõimest, loetakse teda peaaegu et jumalikuks objektiks (substantsiks?). Paljudes religioonides - ristiusk kaasa arvatud - algab maailma ajalugu just valguse loomisest.
|

Kiirte sõltumatus:
ristuvate prozektorikiirte lõikepunktis ei toimu mingit valguse hajumist ega nõrgenemist.
|
|
Laineteooria. Veel enne Newtonit, 1678.a., tuli
prantsuse akadeemik Christiaan Huygens välja teravmeelse, kuid
nõrgalt põhjendatud ideega, et valgus on keskkonna ülikiire
(suure sagedusega) lainetus.
|
Hüpoteesi valguse laineiseloomust püstitas Christiaan Huygens.
|
|
Huygens oli suur võnkumiste uurija,
ka kellapendel on tema leiutatud. Valguse juures meeldis talle
asjaolu, et laine kannab energiat üle ilma osakeste voo abita;
samuti meeldis talle lainete sirgjooneline levimine ning
peegeldus. Ka murdumisseadus annab lainete abil lihtsalt
seletada - kui oletada, et laine levimiskiirus keskkonnas on
pöördvõrdeline murdumisnäitajaga.
Lainete sõltumatus oli
Huygensi pooldajate üks põhiargumente vaidluses Newtoniga ning
seetõttu ei saanud ka Newton seda fakti ignoreerida. Oma
optilisi rehkendusi tegi Huygens geomeetriliselt, kasutades enda
poolt leiutatud printsiipi (tänapäeval tuntud kui Huygens'i
printsiip):
Laine levimisel on iga lainefrondi punkt
laineallikaks; lainefrondi mistahes järgneval ajamomendil saame
leida neist punktidest väljuvate keralainete mähispinnana.
Keeruline lause, aga sirkli abil hästi rakendatav. Ja sobib
suurepäraselt meie ettekujutusega lainest kui korrastatud
võnkumistest.
|
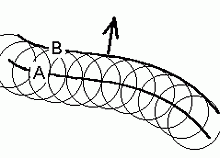
Huygens'i printsiip:
lainefrondi A kõigist punktidest väljuvad keralained tekitavad paralleelse lainefrondi B.
|
|
Fermat' printsiip. Veel paremini kui Huygens oskas
valguskiire teed arvutada teine prantslane Pierre de Fermat.
Tema küll akadeemik ei olnud ja teenis leiba advokaadina, tehes
teadust põhitöö kõrvalt. Elu jooksul kogutud kopsaka varanduse
kohta tegi ta testamendi, mille täitumise üheks tingimuseks oli tema
poolt ette valmistatud käsikirjade avaldamine. Nii ilmusidki
Fermat' tööd alles pärast tema surma 1655. a.
Vormilt on Fermat' printsiip matemaatikute poolt laialt kasutatav variatsiooniprintsiip:
Valguse kiirus keskkonnas on pöördvõrdeline keskkonna
optilise tihedusega; levides punktist 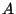 punkti punkti 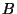 valib
valgus tee, mille läbimiseks kulunud aeg on minimaalne. valib
valgus tee, mille läbimiseks kulunud aeg on minimaalne.
|
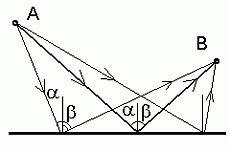
Fermat' printsiip peegeldumisel:
kõigist teedest punktide A ja B vahel on lühim see, kus langemisnurk  on võrdne peegeldumisnurgaga on võrdne peegeldumisnurgaga  . .
|
|
"Optilise tiheduse" all mõistis Fermat' absoluutset
murdumisnäitajat.
Ilmselgeks järelduseks Fermat' printsiibist on
valguse sirgjoonelise levimise seadus. Aga ka peegeldumis- ja
murdumisseadused on lihtsalt rehkendatavad, kui tunneme
funktsiooni ekstreemumi tingimusi. 17. sajandil oli see väga
uus asi.
Muide, variatsioonarvutuse abil võib Fermat' printsiibist
tuletada ka valguskiire tee muutuva optilise tihedusega keskkonnas.
Korpuskulaarteooria. Ja ikkagi tuletas Newton "oma
teooria", pannes optika ummikusse enam kui sajaks aastaks.
|
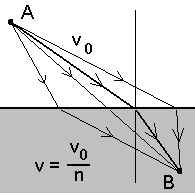
Fermat' printsiip murdumisel.
Kas suudate tõestada, et kiireim tee vastab murdumisseadusele?
|
|
Newtoni järgi on valgus väikeste osakeste - korpusklite (lad.
corpusculum = kehake) - voog. Need osakesed liiguvad väga
suure kiirusega (seetõttu levib valgus sirgjooneliselt) ning on
väga väikesed (seetõttu ei haju nad kiirte lõikumisel). Osakeste
kiirus on kõige väiksem vaakumis ning kasvab ainetes
võrdeliselt optilise tihedusega.
Kõik faktid pea peale pööratud. Miks? Ja miks usuti Newtonit
rohkem kui prantslasi?
|
Newtoni teoorias on valgus väikeste kiirestilendavate osakeste -- korpusklite -- voog.
|
|
Põhjusi oli kaks. Esimene, teaduslik, seisnes selles, et polnud
ühtki vaatluslikku fakti, mis kinnitaks laineteooriat.
Vastupidi:
valgus levib ka vaakumis, aga lainetus nõuab keskkonda.
Lained peavad liitudes interfereeruma (peab kehtima amplituudide
reegel), katses seda ei täheldatud.
Huygensi printsiibist järeldub
difraktsioon (lainetus levib ka tõkete taha), aga valguse teel
olev tõke jätab terava varju.
Täpselt nii Newton väljenduski:
hüpoteese me ei püstita. Muidugi polnud keegi näinud (mõõtnud)
ka korpuskleid, aga nende olemasolu oli igati loogiline.
Teine põhjus on Newtoni autoriteet. Veel tänapäeval on
Cambridge'i ülikoolis, kus Newton oma optikat luges-kirjutas,
alles tema nimeline professuur koos tooliga, mida omal ajal
kasutas Newton. (Tool ise seisab praegu reservis, kuna
professoriks olev Stephen W. Hawking saab kasutada ainult
spetsiaalset elektroonilist ratastooli.)
|
|
|
Etteantud teemas oli
Newtoni traktaat täiuslik. Vast märkasite, et sellest puudub
polarisatsiooni mõiste. See pole juhuslik - kuigi polarisatsiooninähtust tunti juba enne Newtonit, vaikis ta selle maha. Pole ju võimalik seletada kaksikmurdumist korpusklitega.
Loodusteaduses, ka füüsikas, pole kunagi võimalik midagi "ära
teha". Teadus on igavene otsing. Ja ajalugu näitab, et mida põhjalikum on üks või teine teooria, seda põhjalikumalt on ta tunnetusprotsessil jalus.
|
Eitades valguse laineiseloomu, pidurdas Newtoni teooria füüsika arengut rohkem kui sajandi vältel.
|
|
Samal ajal pole midagi praktilisemat heast teooriast.
Näiteks Newtoni omast. Kohe näete.
Geomeetriline optika
Newtoni järgi on valguskiir sirge. Peegeldumisel ja murdumisel
ta muudab suunda, aga see suuna muutus on täpselt arvutatav, kui
teame keskkondade optilisi omadusi (murdumisnäitajat).
|
Geomeetriline optika toetub Newtoni teooriale ja lubab (suhteliselt!) lihtsasti arvutada optiliste süsteemide omadusi.
|
|
Praktilise optika ülesandeks on optiliste riistade
konstrueerimine. Ka tänapäeval on 99% optikast seotud lihtsate
süsteemide - prillide, binoklite, objektiivide jms.
valmistamisega.
Kõik need mahuvad ühe nimetuse alla ja see
nimetus on tsentreeritud optilised süsteemid.
Üldisemas
mõttes tähendab see telgsümmeetriat - kõik
murdvad-peegeldavad pinnad on pöördpinnad ning nendel on
ühine telg.
Kitsamas mõttes (ideaalne optiline süsteem) on
meil tegu ainult sfääriliste või tasapindadega - sel juhul on
tsentreeritud süsteemi tingimuseks sfääride tsentrite asumine
samal sirgel.
|
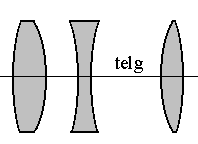
Tsentreeritud optiline süsteem: kõigi läätsede kõverustsentrid asuvad ühel sirgel.
|
|
Ühist telge nimetatakse süsteemi peateljeks. Et kõik
murdvad/peegeldavad pinnad on peatelje suhtes sümmeetrilised,
jääb pärast murdumist (või peegeldust) iga peateljega
paralleelne kiir tasandisse, millel asub ka peatelg. See aga
tähendab, et kiir pärast murdumist/peegeldust lõikub peateljega,
kusjuures lõikepunkti asukoht sõltub nii murdumisnäitajast kui
pinna kõverusest.
- Punkti, kus peateljega paralleelsed kiired lõikavad pärast murdumist
peatelge, nim. pinna fookuseks,
- seda punkti läbivat ja
peateljega ristuvat tasapinda nimetatakse fokaaltasandiks.
|
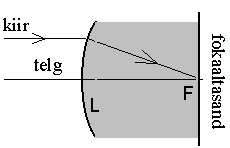
Optilise pinna fokaaltasand ja fookus.
|
Kui
kiir murdub/peegeldub peateljest eemale, leitakse fookus kiire
pikendusel. Loomulikult on teisel pool murdvat pinda veel üks
fokaaltasand (aga peegli korral?).
- Fokaaltasandid on esimene paar süsteemi põhitasanditest.
- Teise paari moodustavad peatasandid
- tasandid, milles
asuvate esemete kujutised süsteemis on esemetega ühesuurused.
- Peatasandite lõikepunkte peateljega nim. peapunktideks.
Fookuste ja peapunktide asukohad on määratud süsteemi ehitusega,
nende arvutamist võib vaadata Saveljevi õpikust (I. Saveljev. Füüsika üldkursus. Tallinn 1979, 3.kd., lk 25 -
45).
Veel paar terminit:
- peapunkti ja fookuse vaheline kaugus on
fookusekaugus,
- selle pöördväärtus on optiline tugevus.
|
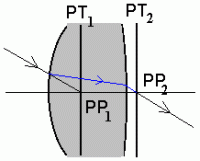
Peatasandid ja peapunktid.
Esimesse peapunkti langev kiir väljub teisest esialgsega paralleelsena(kiire tegelik käik on kujutatud sinisega).
|
|
Edasi on lihtne: teades fookusekaugust ning arvestades, et
- teljega paralleelne kiir läbib pärast murdumist fookuse.
- eesmisse peapunkti langenud kiir väljub tagumisest peapunktist esialgsele paralleelsena,
saame joonlaua abil konstrueerida suvaliste kiirte teekonna läbi kogu süsteemi ning arvutada meid huvitavad suurused geomeetria-trigonomeetria valemite abil. Siit ka meetodi nimetus - geomeetriline optika.
Kui soovime leida mingi punkti kujutist, võtame sellest lähtuvad
kaks kiirt:
- ühe, mis on paralleelne peateljega ja
- teise, mis
suundub peapunkti.
Neid oskame kujutiste ruumis jätkata ning
nende lõikepunkt ongi meie punkti kujutis.
Geomeetriliselt on võimalik teha ka süsteemide
liitmist. Selleks loeme meid huvitava punkti kujutise esimeses süsteemis teise süsteemi lähtepunktiks ning konstrueerime sama eeskirja kohaselt selle kujutise teises süsteemis. Nii võime jätkata lõpmatuseni.
|
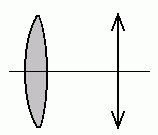
Reaalne ja "õhuke" lääts:
viimasel kujutatakse ainult peatasand.
|
|
Seega vaadeldakse süsteemide liitmisel esimese süsteemi poolt tekitatud
kujutist teise süsteemi objektina. Selle kujutis
teises süsteemis ongi eseme kujutiseks liitsüsteemis.
Muidugi on see vaid skeem; reaalsete kiirte tee erineb oluliselt kiirte käigust ideaalses
süsteemis.
Kooliülesannetes kasutatakse tavaliselt süsteemi graafilist kujutist, kus peatasandid viiakse
kokku üheks tasandiks - nn. "õhukeseks läätseks" (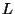 ). ).
Sellises läätses on pilt pööratav: ühtviisi saame
konstrueerida objekti järgi kujutise (ülemine kiir) või siis
kujujtise järgi objekti (alumine kiir).
|
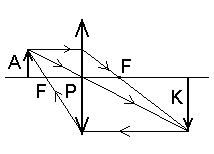
Kujutise konstrueerimine läätses.
A - ese, K - kujutis, F - fookus, P - peapunkt
|
|
Süsteemi põhiparameetrid. Optilise süsteemi põhiparameetriteks on fookusekaugus, suurendus ja valgusjõud.
Fookusekaugus defineeritakse analoogiliselt
optilise pinna omaga:
- fookus on punkt optilisel teljel, kuhu koonduvad
teljega paralleelsed kiired;
- fookusekaugus on fookuse kaugus läätse (süsteemi viimase, fookusele lähima elemendi)
tasandist.
Suurendus on mõistetav kaheti:
- kujutise
lineaarmõõtmete suhet objekti mõõtmetesse nim.
joonsuurenduseks,
- kujutise ja objekti vaatenurkade suhet aga
nurksuurenduseks ehk lihtsalt suurenduseks.
Et optilist tsentrit läbiv
kiir oma suunda ei muuda, moodustub sarnaste kolmnurkade paar,
kust
Neist ühe (tavaliselt kujutise kauguse) saame asendada läätse valemist
Näeme, et
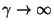 , kui , kui
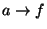 ning ning
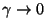 , kui , kui
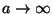 .
Joonsuurendus
on oluline fotokaamerate ning projektsiooniseadmete korral.
Visuaalsel (silmaga) vaatlemisel on tähtsam nurksuurendus. .
Joonsuurendus
on oluline fotokaamerate ning projektsiooniseadmete korral.
Visuaalsel (silmaga) vaatlemisel on tähtsam nurksuurendus.
Nurksuurenduse valemid tuletage ise. Kui vaja, vaadake
kooliõpikust järele.
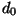 tähistab nn. "parima nägemise kaugust" - normaalse silma jaoks on tähistab nn. "parima nägemise kaugust" - normaalse silma jaoks on 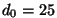 cm. cm.
|
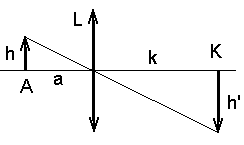
Joonsuurendus.
A - ese, K - kujutis, L - lääts
|
|
Valgusjõud iseloomustab kujutise valgustatust
objektiga võrreldes. Selle leidmiseks võrdleme objekti heledust
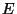 kujutise heledusega kujutise heledusega 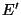 . Lihtsuse mõttes võtame objektiks
mati pinna, mis kiirgab ühtlaselt tema kohale jäävasse
ruuminurka . Lihtsuse mõttes võtame objektiks
mati pinna, mis kiirgab ühtlaselt tema kohale jäävasse
ruuminurka 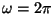 .
Olgu objekti pinna suurus .
Olgu objekti pinna suurus 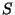 , siis
jõuab tema kiirgusest ( , siis
jõuab tema kiirgusest (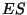 ) objektini vaid see osa, mis vastab
objektiivi pindalale (objektilt vaadatuna) ) objektini vaid see osa, mis vastab
objektiivi pindalale (objektilt vaadatuna)
|
Süsteemi valgusjõud näitab, kuimitu korda on kujutise pind heledam objekti omast. Ta on võrdeline süsteemi suhtelise ava ruuduga.
|
kus 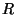 on objektiivi raadius ja on objektiivi raadius ja 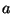 objekti kaugus
objektiivist. Optiline süsteem annab sellest kujutise pindalaga objekti kaugus
objektiivist. Optiline süsteem annab sellest kujutise pindalaga
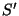 ning heledusega ning heledusega 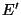 , kusjuures , kusjuures 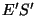 peab olema võrdne
eseme poolt objektiivile kiiratud valgusega: peab olema võrdne
eseme poolt objektiivile kiiratud valgusega:
Kujutise ja objekti heleduste suhteks saame seega
ning, arvestades joonsuurendust
Saame
Avaldist 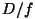 , kus , kus 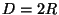 on objektiivi läbimõõt, nim. süsteemi
(objektiivi) suhteliseks avaks. Näeme, et valgusjõud on
võrdeline suhtelise ava ruuduga. on objektiivi läbimõõt, nim. süsteemi
(objektiivi) suhteliseks avaks. Näeme, et valgusjõud on
võrdeline suhtelise ava ruuduga.
|
|
|
Aberratsioonid. Geomeetriline optika, nagu teisedki füüsikateooriad, on
matemaatiliselt ilus ja lihtne ainult idealiseeritud juhul
(õhukesed läätsed, optilise peateljega paralleelsed kiired,
väike suhteline ava jms). Reaalsete süsteemide korral
pole meil enamik nendest täidetud. Seetõttu annab geomeetriline
optika vaid lähtevõrrandid, mida tuleb "parandada" nn. optiliste
vigade ehk aberratsioonide arvel.
Iga kõrvalekallet
ideaalsest süsteemist kajastab omaette aberratsioon:
- kromaatiline aberratsioon on fookusekauguse sõltuvus lainepikkusest;
- sfääriline aberratsioon on fookusekauguse sõltuvus kiire kaugusest optilisest teljest
(sfäärilise läätse või peegli korral);
|
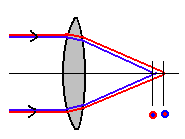
Kromaatiline aberratsioon: kuna punaste kiirte jaoks on klaasi murdumisnäitaja väiksem, asub nende koondumispunkt (fookus) läätsest kaugemal kui sinistel kiirtel.
|
- astigmatism on kujutise moondumine juhul, kui kiired pole paralleelsed optilise
peateljega;
jne. jne.
Aberratsioonide teooria on vähemalt niisama
keeruline kui geomeetriline optika ise. Et vigade parandamiseks
tehtavate arvutuste maht oli suur ja täpsus väike, oli
praktiline optika kuni viimase ajani suures osas "kunst", kus
meistri kogemused ja vilumus kaalusid tihti üles inseneride
suured arvutused.
1980-test alates on põhiliselt tänu jaapani ja USA tehnoloogiale
kujunemas automatiseeritud optikatööstus, kus optilisi süsteeme
enam ei arvutata, vaid modelleeritakse arvuti abil. Arvuti
juhtimisel ja laserseadme kontrolli all toimub ka tulemuse
realiseerimine.
|
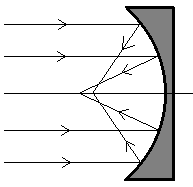
Sfääriline aberratsioon: optilisest peateljest kaugemal asuvad paralleelsed kiired lõikavad pärast peegeldumist telge peeglile lähemal.
|
|
Fotograafias ja astronoomias on revolutsioon
juba toimunud - programmeeritav tehnoloogia võimaldab saada
suvaliste parameetritega optikat. Viimaseks moeks on nn.
adapteeruv optika, kus pinna kuju on muudetav ka
ekspluatatsiooni käigus (isefokuseeruvad teleskoobid ja kaamerad, kujutise stabiliseerimine binoklis või liikuva kaamera korral).
|
|
|
Fotomeetria.
Kui tõlkida ladina keelest, tähendab fotomeetria valguse
mõõtmist. Sõnal "valgus" on aga, nagu teame, kaks tähendust:
- elektromagnetkiirgus kindlas sagedusvahemikus;
- valgusaisting.
|
Fotomeetria tegeleb valguse mõõtmisega.
|
|
Aistingu tugevust pole võimalik mõõta, kogu
füüsika ongi tehtud just aistingute
ebaobjektiivsusest
vabanemiseks. Sellele vaatamata oleks hea, kui oskaksime
kirjeldada todasama elektromagnetkiirgust suurustega, mis
võimalikult hästi korreleeruksid selle lainetuse poolt esile
kutsutud aistingu tugevusega.
Fotomeetrias defineeritakse valgustugevuse ühikud, mis sobivad
normaalse "keskmise" inimese nägemisega. Neid kasutatakse töö-
ja eluruumide ning tänavavalgustuse projekteerimise
normatiividena, samuti valgustite tehnilisel kirjeldamisel.
Füüsikalistel mõõtmistel kasutatakse seevastu energeetilisi
suurusi, millel pole nägemisega midagi ühist. Loomulikult on olemas ka
ilus integraal ühtedelt ühikutelt teistele üle minemiseks.
|
|
|
Energeetilised ühikud on SI-süsteemis nagu ikka vatt
(W) ja vatt ruutmeetri kohta (W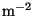 ). ).
Vattides mõõdetakse pinna bolomeetrilist heledust.
Teades kiirgava keha pindala, võime selle abil arvutada kiirgaja koguvõimsuse:
|
Energeetilised ühikud:
- vatt (W)
- vatt ruutmeetri kohta (W/m2)
|
Energiavoog arvutatakse tavaliselt aga Gaussi teoreemi abil: (energia)voog läbi kinnise pinna on
võrdne pinnaga ümbritsetud ruumis asuvate (energia)allikate
koguvõimsusega:
Ühe allika
ning isotroopse kiirguse korral järeldub sellest (nagu jõuväljade korralgi),
pöördruutsõltuvus. See tähendab, et küllalt suurel kaugusel allikast on
"Suurel kaugusel" tähendab seda, et me ei pea arvestama allika
mõõtmeid. Analoogiliselt gravitasioonivälja punktmassi või elektrivälja punktlaenguga räägitakse siingi punktallikast.
Selle lähendi abil on lihtne defineerida näiteks
allika bolomeetrilise valgustugevuse, mis on võrdne ühikulisse
ruuminurka (sterradiaani) kiiratud energiaga:
Kordaja 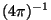 võtmisel ühiku definitsiooni sisse on
sügav mõte: nüüd saame kaugusel võtmisel ühiku definitsiooni sisse on
sügav mõte: nüüd saame kaugusel 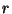 asuvat ühikulist pinda
läbiva kiirgusvoo, jagades heleduse pinna kauguse ruuduga (ühte
sterradiaani kiiratud valgus jaotub kaugusel asuvat ühikulist pinda
läbiva kiirgusvoo, jagades heleduse pinna kauguse ruuduga (ühte
sterradiaani kiiratud valgus jaotub kaugusel 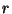 ühtlaselt
pinnale ühtlaselt
pinnale 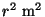 ). Pinna võimalikku kallet arvestades: ). Pinna võimalikku kallet arvestades:
kus 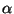 on langemisnurk (nurk kiirte suuna ja pinnanormaali
vahel).
Suurust on langemisnurk (nurk kiirte suuna ja pinnanormaali
vahel).
Suurust 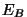 nim. pinna bolomeetriliseks
valgustatuseks.
Tema ühikuks ongi vatt ruutmeetri kohta. Sama ühik kõlbab veel kiirgava pinna kiirgusvõime
ja ruumis asuvat pinda läbiva kiirgusvoo kirjeldamiseks. nim. pinna bolomeetriliseks
valgustatuseks.
Tema ühikuks ongi vatt ruutmeetri kohta. Sama ühik kõlbab veel kiirgava pinna kiirgusvõime
ja ruumis asuvat pinda läbiva kiirgusvoo kirjeldamiseks.
Nüüd ongi meil käes põhilised suurused ja
seosed nende vahel. Jääb üle seletada, mida tähendab indeks 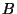 ja täiend "bolomeetriline". Õigem oleks öelda
"energeetiline" valgustatus, aga ajalooliselt on jäänud viide soojuslikule
kiirgusvastuvõtjale - bolomeetrile. Algselt oli bolomeeter
tumedaks värvitud anum, milles oleva vedeliku temperatuuri
mõõtes hinnati anuma poolt neelatud kiirguse energiat; praegu
nimetatakse nii kõiki soojusliku toimega kiirgusmõõtjaid.
ja täiend "bolomeetriline". Õigem oleks öelda
"energeetiline" valgustatus, aga ajalooliselt on jäänud viide soojuslikule
kiirgusvastuvõtjale - bolomeetrile. Algselt oli bolomeeter
tumedaks värvitud anum, milles oleva vedeliku temperatuuri
mõõtes hinnati anuma poolt neelatud kiirguse energiat; praegu
nimetatakse nii kõiki soojusliku toimega kiirgusmõõtjaid.
|
|
|
Fotomeetrilised ühikud. Kui on vaja mõõta kiirguse
intensiivsust inimsilmas tekkiva valgusaistingu alusel, tuleb
energeetilisi ühikuid teisendada. Selleks korrutame suvalist
nendest erilise funktsiooni, nn. silma tundlikkuse
kõveraga.
See on katseliselt, suure hulga inimeste abiga
koostatud funktsioon, mis kujutab sama energiaga kiirguse
poolt tekitatud aistingu tugevuse sõltuvust valguse
lainepikkusest.
Funktsioon on normeeritud nii, et ta võrdub
ühega silma maksimaalse tundlikkuse juures (
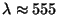 nm) ning on null seal kus silm kiirgust ei tunne. Kõvera
nm) ning on null seal kus silm kiirgust ei tunne. Kõvera
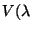 käik on antud kõrvalasuval joonisel. käik on antud kõrvalasuval joonisel.
|
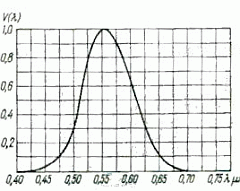
Silma valgustundlikkuse kõver.
|
|
See pole veel kõik. Loomulikult on ka valguse mõõtmisel (nagu
mujalgi füüsikas) mõõtühikud vanemad kui teooria. Seetõttu ei
mõõda me valgusvoogu mitte "bioloogiliste vattide", vaid
luumenitega, valgustatust luksides, valgustugevust
kandelates ning kiirgava pinna heledust nittides.
Põhiühikuks on valgustugevuse ühik kandela e.
rahvusvaheline küünal (cd), mille kohta antakse etaloondefinitsioon:
|
SI süsteemi fotomeetriliseks põhiühikuks on kandela.
|
Üks kandela on valgustugevus, mis võrdub 1/60
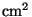 suuruse pinna kiirgusega plaatina
tahkumistemperatuuril (2044 K). suuruse pinna kiirgusega plaatina
tahkumistemperatuuril (2044 K).
Tuletatud ühikuteks on:
- Luumen (lm) - valgusvoog, mida
kiirgab punktallikas 1 cd ruuminurka 1 sterradiaan;
- Luks (lx) vastab valgustatusele üks luumen ruutmeetri kohta;
- nitt (nt) vastab heledusele 1 cd kiirgava pinna ruutmeetri kohta.
Kõik
"energeetilised" valemid kehtivad ka "fotomeetriliste" suuruste
kohta.
|
Fotomeetrilised ühikud:
- kandela (cd)
- luumen (lm)
- luks (lx)
- nitt (nt).
|
|
Juhul, kui valgusallikat pole võimalik "väikseks" lugeda, tuleb
kasutada vana tuttavat võtet. Allika (näiteks suuremõõtmelise
hajutiga lambi) pind jagatakse elementideks, millest igaühte
võib vaadelda kui punktallikat; seejärel leitakse vaadeldava pinna
valgustatus kõigi elementide jaoks ning summeeritakse.
Tavaliselt on tulemuseks integraal üle mingi geomeetrilise
pinna.
Pisut keerulisem on juht, kus pinnalt lähtuv kiirgus pole
isotroopne - sel juhul tuleb valgustatuse valemisse lisaks
langemisnurgale veel kiirgaja indikatrissist (funktsioon,
mis kirjeldab eri suundades kiiratavate lainete suhtelisi
intensiivsuseid) tulenev kordaja.
Hästi on uuritud nn.
koosinuskiirgajat, kus pind kiirgab ühtlaselt kõigis suundades,
mistõttu indikatrissi asemel läheb valemisse pinna kaldenurk.
Koosinuskiirgaja korral vastab pinna heledusele (kiirgusvõime
pinna ühelt ruutmeetrilt ruuminurka üks sterradiaan) üks nitt
valgsus (kogukiirgus ühelt ruutmeetrilt) 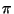 kandelat. kandelat.
Energeetiliste ning fotomeetriliste ühikute võrdluseks võib tuua
ühe arvu: parima nägemise lainepikkusel (555 nm) vastab valgusvoole
üks luumen kiirgusvoog 0.0016 W/ster.
|
|
|
Akustika. Ka kuulmisaisting on laine
(seekord õhus või vees leviva elastsuslaine) poolt edasikantava
energia tajumine. Seetõttu tekib ka siin vajadus taju mõõtmiseks
- näiteks töökaitses müra piirnormi rehkendamisel.
Nagu valguse, nii ka hääle korral sõltub aisting energiavoost ja
sagedusest. Ainult et erinevalt silmast pole võimalik kõrvu
ülemäärase heli eest kaitsmiseks sulgeda.
|
Akustika on tehnilise füüsika haru, mis uurib häälelainete levimist. Kitsamas mõttes uurib ta häälelainete poolt esile kutsutavat kuulmisaistingut.
|
|
Seetõttu piirab
kuuldepiirkonda lisaks tundlikkusele (alumine kõver joonisel)
veel nn. valulävi, millest suurema energiavoo toimel tekib
organismi kaitsereaktsioonina valuaisting (ülemine kõver).
"Normaalse kuuldavuse" piirkond jääb kusagile nende kahe kõvera
vahele.
Muide, valulävi toimib ka kuuldepiirkonnast väiksema
sageduse (nn. infraheli) korral ja seda arvestab
vibratsioonikaitse. Samuti on bioloogiline mõju suurematel
sagedustel, aga sellekohased normatiivid ei puutu ei akustikasse
ega fotomeetriasse. Nende probleemidega tegeleb
kiirguskaitse, millel on omad bioloogilist laadi mõõtühikud.
Parima kuulmise sagedusel (umbes 1000 Hz) on valu-
ja kuuldelävele vastavate energiavoogude suhe 13 suurusjärku. Et
seda mõistlikult gradueerida, võetakse kasutusele
logaritmilised ühikud. Heli valjuse ühikuks on bell (B)
ja selle arvutamise valem on
|
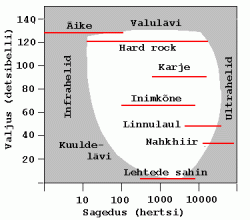
Kuuldepiirkond. Kuulmislävest nõrgemad helid kuulmisaistingut ei tekita, valulävest tugevamate helide korral tekib valuaisting.
|
Tavaliselt kasutatakse belli asemel 10 korda väiksemat ühikut -
detsibelli. Kui soovime vastust detsibellides, tuleb valemit
korrutada kümnega. Rangelt võttes kehtib valem vaid 1000 Hz
lähedaste sageduste korral; et aga kõrva tundlikkus sellest
eemaldumisel kiiresti langeb, võib integraali asendada
keskväärtusega, mis erineb tegelikust vaid poole detsibelli võrra.
Huvitav on märkida, et astronoomide kasutatav tähesuuruste
skaala on üsna sarnane akustilisele. Kui võtta aluseks kindlasse
(silma või valgusfiltri abil määratud)
sageduspiirkonda jääv energiavoog, on tähesuurus määratud valemiga:
Konstant 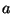 on määratud mõõteriistaga, funktsioon on määratud mõõteriistaga, funktsioon
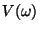 on aga meile juba tuttav silma (või filtri) tunnuskõver - seekord mitte lainepikkuse vaid nurksageduse järgi. on aga meile juba tuttav silma (või filtri) tunnuskõver - seekord mitte lainepikkuse vaid nurksageduse järgi.
|
"Keskmise inimese" aistinguid hindavaid mõõtühikuid nimetatakse mõnikord biomeetrilisteks.
Sellega rõhutatakse, et mõõdetakse mitte niivõrd nähtusi (heli, valgus) kui neid tajuvaid organisme (näiteks inimesi).
Heli valjuse ühikuks on bell (B). Tavaliselt mõõdetakse valjust detsibellides.
Valjuse skaala on logaritmiline:
mõõtühik käib mitte energiavoo, vaid selle logaritmi kohta.
|
![]() Optika neli põhiseadust
Optika neli põhiseadust
![]() Ajaloost
Ajaloost
![]() Laineteooria
Laineteooria
![]() Fermat' printsiip
Fermat' printsiip
![]() Korpuskulaarteooria
Korpuskulaarteooria
![]() Geomeetriline optika
Geomeetriline optika
![]() Tsentreeritud optiline süsteem
Tsentreeritud optiline süsteem
![]() Süsteemi põhiparameetrid
Süsteemi põhiparameetrid
![]() Fookusekaugus
Fookusekaugus
![]() Suurendus
Suurendus
![]() Valgusjõud
Valgusjõud
![]() Aberratsioonid
Aberratsioonid
![]() Fotomeetria
Fotomeetria
![]() Energeetilised ühikud
Energeetilised ühikud
![]() Fotomeetrilised ühikud
Fotomeetrilised ühikud
![]() Akustika
Akustika
![]()