Loeng 14. Mehaanilised ja elektrivõnked.
Perioodiline liikumine.
Perioodiliseks liikumiseks (protsessiks) nimetame sellist
liikumist, mis kordub teatud kindla ajavahemiku -
perioodi - järel. Igapäevaelus kipume nimetama perioodiliseks
igasuguseid korduvaid nähtusi (aastaajad, bussiliiklus,
palgapäevad); füüsikas loeme protsessi perioodiliseks vaid siis,
kui kehtib matemaatiline seos
kus muutuja 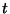 tähistab aega, konstant tähistab aega, konstant 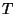 perioodiks
nimetatavat ajavahemikku, perioodiks
nimetatavat ajavahemikku, 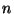 nagu tavaliselt, täisarvu.
Definitsioon langeb täielikult ühte matemaatika perioodiliste
funktsioonide omaga; füüsikas peab argumendiks olema aeg.
(Muidu poleks tegu protsessiga.) nagu tavaliselt, täisarvu.
Definitsioon langeb täielikult ühte matemaatika perioodiliste
funktsioonide omaga; füüsikas peab argumendiks olema aeg.
(Muidu poleks tegu protsessiga.)
|
Perioodiliseks protsessiks nimetatakse protsessi, mis mis kordub kõigis üksikasjades teatud ajavahemiku (perioodi) järel.
|
|
Perioodilistest liikumistest tunneme seni
pöörlemist, täpsemalt ühtlast pöörlemist. Kui pöörlemine
on kiirenev või aeglustuv, pole meil võimalik näidata
konstantset perioodi, ehkki liikumine ajas kordub. Nagu näeme,
on perioodiline liikumine mõnes mõttes ühtlase sirgliikumise
analoog - viimase fundamentaalset tähtsust rõhutas Newton oma
esimeses seaduses.
|
Perioodilise liikumise lihtsaimad näited on ühtlane pöörlemine ja harmooniline võnkumine (SHM).
|
Lainefüüsikat õppides näeme, et niisama fundamentaalne on ka nn.
harmooniline liikumine (ingl. Simple Harmonic Motion, lühendina SHM) - võnkumine, mille periood ei sõltu mingitest
välistest teguritest. Väga paljud nähtused on hästi
kirjeldatavad konstantse perioodiga võnkumiste abil.
Sõna
"harmooniline" pärineb ise muusikast, mis oli vanasti üks
füüsika osi. Muusikas tähendab harmoonia helide tonaalsuste
sobivust - nagu selgub, on seegi kirjeldatav püsiva sagedusega
võnkumiste abil.
Loodus pakub meile tohutult näiteid võnkuvate kehade või
süsteemide kohta. Iga keha (süsteem), mis on püsivas
tasakaalus, hakkab pärast tasakaalust välja viimist võnkuma.
Need pole küll ilmtingimata harmoonilised võnked, kuid peaaegu
alati on olemas kindel sagedus, mis sõltub võnkumisvõimelise
süsteemi parameetritest. Ja nagu tavaliselt, võime konstrueerida
protsessi (süsteemi) idealiseeritud mudeli, mis liigub täpselt
harmoonilise võnkumise seaduse järgi ning kus kogu
"mitteharmoonilisus" viiakse muutuvatesse parameetritesse.
|
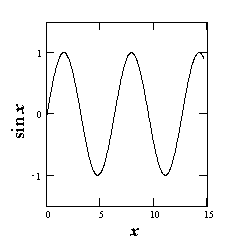
Siinusvõnked x=sin(t) kui harmoonilise liikumise näide.
|
|
Kehade (süsteemi) tasakaalu tingimused.
Dünaamikas tähendab tasakaal seda, et keha ei muuda oma
olekut. Newtoni seaduste järgi tähendab see jõudude puudumist
(või nende vastastikust kompenseerumist). Matemaatiliselt
väljendab seda kehale mõjuvate jõudude ning jõumomentide
algebralise (vektor-) summa võrdumine nulliga:
|
Tasakaaluasendis on kehale mõjuvate jõudude, samuti jõumomentide algebraline summa null.
|
|
Tasakaalus oleva keha jaoks on alati olemas inertsiaalsüsteem,
milles selle keha masskese on paigal. Keha ise võib seejuures
pöörelda konstantse nurkkiirusega (ühtlane pöörlemine).
Sama kehtib kehade süsteemi kohta. Sellisel juhul on
nõutav kõigile kehadele mõjuvate resultantjõudude
(jõumomentide) võrdumine nulliga.
Need definitsioonid, ehkki absoluutsed, ei ütle midagi tasakaalu
püsivuse kohta. Ometi teame, et seinale riputatud vikat on
tunduvalt ohutum seina najale pandud vikatist - viimane võib
juba kergest tõukest alla kukkuda. Selle kohta annab
koolifüüsika reegli: keha on püsivas tasakaalus, kui tema
raskuskese asub allpool toetuspunkti. Päris õige see pole, kuna
enamus Maa raskusjõu väljas olevaid kehasid (näiteks lauale
pandud tikutoos) püsib hästi paigal vaatamata sellele, et
masskese on toetuspinnast kõrgemal.
|
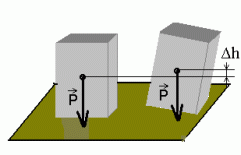
Tikutoos laual: et toos külili kukuks, tuleb ta kõigepealt serva peale keerata. Kuna sel ajal raskuskese tõuseb, suureneb ka potentsiaalne energia.
|
Teoreetilises mehaanikas lahendatakse tasakaalu küsimus energia
abil. Konservatiivsete jõudude korral väljendab seda
potentsiaalse energia miinimumi lause:
Keha on püsivas tasakaalus, kui tema potentsiaalne
energia on minimaalne
Niisiis: tasakaal on püsiv juhul, kui keha liigutamiseks
tasakaaluasendist tuleb teha tööd - suurendada energiat.
Energia kohta kehtib võrdus
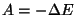 - kui süsteem teeb tööd, peab tema energia
vähenema ja vastupidi, et energia suureneks, peab tehtama tööd
süsteemi jõudude vastu.
Töö valemist - kui süsteem teeb tööd, peab tema energia
vähenema ja vastupidi, et energia suureneks, peab tehtama tööd
süsteemi jõudude vastu.
Töö valemist
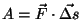 näeme, et viimasel juhul peab kahe vektori skalaarkorrutis olema
negatiivne, st vektorid näeme, et viimasel juhul peab kahe vektori skalaarkorrutis olema
negatiivne, st vektorid 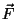 ja ja
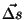 peavad olema vastassuunalised.
peavad olema vastassuunalised.
|
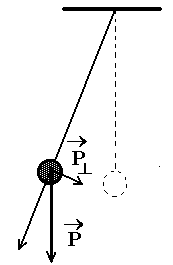
Direktsioonijõu teke: tasakaalust välja viidud pendlikuulile mõjuva raskusjõu 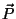 komponent komponent 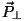 on suunatud tasakaaluasendi poole. on suunatud tasakaaluasendi poole.
|
Jõudsimegi võnkumiste fundamentaalse seaduseni: selleks, et
tasakaal oleks püsiv, peab keha väljaviimisel tasakaaluasendist
tekkima jõud, mis püüab viia keha tagasi tasakaaluasendisse.
Seda jõudu nimetatakse direktsioonijõuks. Direktsioonijõu
olemasolu on võnkumiste tekke hädavajalik tingimus.
Ühemõõtmelise liikumise korral saab toodut illustreerida graafiliselt
teljestikus "potentsiaalne energia - asukoht (ruumikoordinaat)".
Joonisel toodud kõveratest vastab ülemine püsivale, alumine aga
ebapüsivale tasakaalule. Näeme, et keha nihutamisel tasakaaluasendist
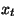 eemale ülemisel graafikul potentsiaalne energia suureneb. Tekkiv
jõud eemale ülemisel graafikul potentsiaalne energia suureneb. Tekkiv
jõud
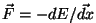 on suunatud tasakaaluasendi poole, tema
suurus ning sõltuvus kaugusest tasakaaluasendini on suunatud tasakaaluasendi poole, tema
suurus ning sõltuvus kaugusest tasakaaluasendini
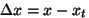 olenevad funktsiooni
olenevad funktsiooni 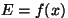 omadustest (potentsiaalikõvera kujust).
Alumisel kõveral kutsub aga vähimgi eemaldumine tasakaalupunktist
esile jõu, mis sunnib keha sealt lõplikult lahkuma omadustest (potentsiaalikõvera kujust).
Alumisel kõveral kutsub aga vähimgi eemaldumine tasakaalupunktist
esile jõu, mis sunnib keha sealt lõplikult lahkuma
Kui kehale rohkem jõudusid ei mõju, tähendab energia kasvatamine
nihkel
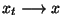 keha (süsteemi) koguenergia kasvu
tasemeni keha (süsteemi) koguenergia kasvu
tasemeni 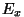 . .
Sellise energiaga keha võib vabalt liikuda ruumipunktide
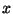 ja ja 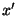 vahelises piirkonnas, kusjuures tema kineetiline energia
mingis punktis vahelises piirkonnas, kusjuures tema kineetiline energia
mingis punktis 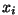 vastab energiate vahele vastab energiate vahele 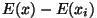 . Meie
(ühemõõtmelisel) juhul on ainus võimalik liikumistüüp võnkumine
punktide . Meie
(ühemõõtmelisel) juhul on ainus võimalik liikumistüüp võnkumine
punktide 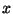 ja ja 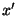 vahel. vahel.
|
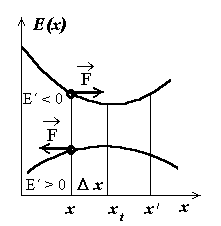
Potentsiaalikõverad: püsiv tasakaal (ülemine kõver) ja ebapüsiv tasakaal (alumine kõver). Jõu suund sõltub tuletise märgist.
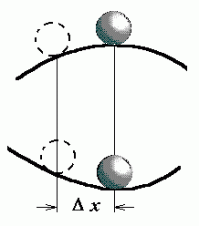
Pall mäe otsas ja oru põhjas. Kaugusele 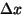 nihutatud pall veereb esimesel juhul tasakaaluasendist eemale, teisel juhul tagasi oru põhja. nihutatud pall veereb esimesel juhul tasakaaluasendist eemale, teisel juhul tagasi oru põhja.
|
Vabavõnked ja harmoonilised võnked.
Süsteemi vabavõngeteks nimetame liikumisi, mis toimuvad
tasakaaluasendist väljaviimisel tekkiva
direktsioonijõu mõjul.
Direktsioonijõud on suunatud
tasakaaluasendi poole ja sõltub võnkuva keha kaugusest
tasakaaluasendist - nn hälbest.
Kui direktsioonijõud on
võrdeline hälbega, tekib lihtsaim võnkumistest -
siinusvõnked.
|
Harmooniline liikumine (siinusvõnked) tekib siis, kui direktsioonijõud on võrdeline hälbega.
|
|
Vaatleme näiteks vedru otsa riputatud raskust.
Oletame, et raskusele massiga
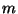 mõjub
raskusjõud mõjub
raskusjõud 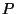 , mille tasakaalustab vedru elastsusjõud , mille tasakaalustab vedru elastsusjõud 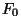 .
Kui vedru viiakse tasakaaluasendist välja, venitades teda
pikkuse .
Kui vedru viiakse tasakaaluasendist välja, venitades teda
pikkuse 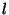 võrra, suureneb elastsusjõud väärtuse võrra, suureneb elastsusjõud väärtuse 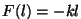 võrra. Et enne venitamist olid jõud tasakaalus, väljendab see
juurdekasv raskusele mõjuvat jõudu, kutsudes esile kiirenduse
võrra. Et enne venitamist olid jõud tasakaalus, väljendab see
juurdekasv raskusele mõjuvat jõudu, kutsudes esile kiirenduse
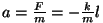 . Arvestades, et . Arvestades, et
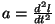 ,
saame liikumisvõrrandiks ,
saame liikumisvõrrandiks
Lihtsa proovimisega saab näidata, et seda võrrandit
rahuldavad funktsioonid 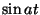 ning ning 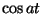 juhul, kui juhul, kui
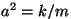 . Peale selle "lihtsa" lahendi kõlbavad kõik funktsioonid . Peale selle "lihtsa" lahendi kõlbavad kõik funktsioonid
See ongi harmooniliste võngete võrrand.
|
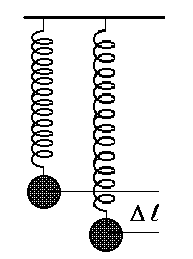
Vedrupendel. Direktsioonijõuks on elestsusjõud, mis Hooke'i seaduse järgi on võrdeline ja vastassuunaline deformatsiooni, st. hälbega (kaugusega tasakaaluasendist).
|
Võnkumist iseloomustavad suurused.
- Võnkumiste
konstandid - parameetrid, mis ajas ei muutu:
suurust 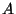 ,
mis väljendab võnkuva keha maksimaalset kõrvalekallet
tasakaaluasendist, nimetatakse amplituudiks.
aja ,
mis väljendab võnkuva keha maksimaalset kõrvalekallet
tasakaaluasendist, nimetatakse amplituudiks.
aja 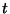 kordajat kordajat
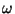 nimetetakse võnkumise nurksageduseks.
liidetavat nimetetakse võnkumise nurksageduseks.
liidetavat
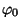 nimetatakse algfaasiks. nimetatakse algfaasiks.
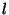 -- hälve (kaugus tasakaaluasendist hetkel -- hälve (kaugus tasakaaluasendist hetkel 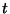 )
siinuse argumenti )
siinuse argumenti
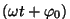 nimetame
faasiks. nimetame
faasiks.
|
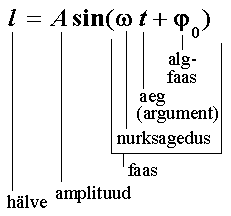
Harmooniliste võngete võrrand ja selle elemendid.
|
Algfaas on seega võnkuva keha faas hetkel
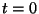 , amplituud aga maksimaalne hälve. , amplituud aga maksimaalne hälve.
Seda, et tegemist on perioodilise liikumisega, järeldame
siinusfunktsiooni (või koosinuse) perioodilisusest. Et nende
funktsioonide periood on 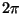 , tuleb võnkeperioodiks
faas , tuleb võnkeperioodiks
faas 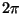 : :
Seega on ajaline periood:
Tihti avaldatakse hoopis 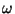 perioodi kaudu: perioodi kaudu:
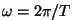 . .
Võnkeperioodi pöördväärtust
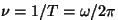 nim.
võnkesageduseks. nim.
võnkesageduseks.
Nüüd peaks kõik olema. Nende suurustega kirjeldatakse füüsikas
harmoonilisi võnkumisi.
|
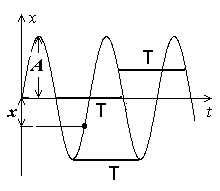
Harmooniliste võnkumiste graafik. Lõik T väljendab (võnke)perioodi.
|
Faasidiagramm ja võnkumiste liitmine
Võnkumiste liitmist vajame siis, kui üks ja seesama keha võtab
osa mitmest sõltumatust võnkumisest. Et leida summaarse
liikumise valemit, peame need võnkumised liitma.
Lihtne harmooniline võnkumine on ühesuunaline. Seetõttu
võisime teda kirjeldada ühedimensionaalse liikumisena. Kui keha
osaleb kahes võnkumises, ei tarvitse nende suunad ühte langeda
- seetõttu peame nad kirjeldama vektoritena.
|
Keha võib samaaegselt osaleda kuitahes mitmes võnkumises. Koguliikumise saame, kui liidame kõik need võnkumised, arvestades liikumissuunda.
|
|
Samal kombel liidame vektoritena ka kolm või rohkem võnkumist.
Loomulikult võime kasutada koordinaatmeetodit, liites vektorite
asemel nende komponente.
Seetõttu taandub võnkumiste liitmine
suundade järgi kahele põhijuhule: samasihiliste ja
ristuvate võnkumiste liitmisele.
A. Samasihilised võnkumised.
1.
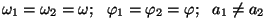 Toimub summaarse amplituudiga võnkumine:
Toimub summaarse amplituudiga võnkumine:
2.
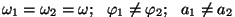 Kui amplituudid on võrdsed, saame hakkama trigonomeetria
valemite abil (kuidas?). Kui mitte, kasutame faasidiagrammi.
Kui amplituudid on võrdsed, saame hakkama trigonomeetria
valemite abil (kuidas?). Kui mitte, kasutame faasidiagrammi.
Mis see on? Iga harmoonilist võnkumist saab kujutada pöörlemisena.
Selleks joonistame vektori pikkusega (mooduliga!) 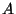 ning vaatame,
kuidas muutub tema ning vaatame,
kuidas muutub tema 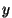 -koordinaat juhul, kui vektor pöörleb ühtlase
nurkkiirusega -koordinaat juhul, kui vektor pöörleb ühtlase
nurkkiirusega 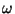 oma alguspunkti ümber. Lihtsaimal juhul, kui
vektor algab koordinaatide alguspunktist oma alguspunkti ümber. Lihtsaimal juhul, kui
vektor algab koordinaatide alguspunktist 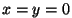 , saame , saame
|
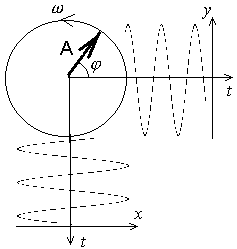
Faasidiagramm (Phasor).
Ümber koordinaatide alguspunkti pöörleva vektori x- ja y-komponendid muutuvad harmoonilise liikumise valemi kohaselt.
|
kus 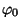 on meie vektori on meie vektori 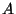 nurk nurk 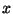 -teljega hetkel -teljega hetkel 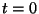 . .
Aga see ongi ju harmooniliste võnkumiste võrrand.
Võnkumise
graafilist kujutamist pöörleva vektorina nimetatakse
faasidiagrammiks (ingl. phasor).
See annab meile hea
võimaluse asendada küllaltki keeruline valemite liitmine märksa
piltlikuma vektorite liitmisega.
Joonistame kaks ühest punktist lähtuvat vektorit, millede moodulid on
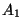 ja ja 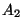 ning nurgad ning nurgad 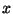 -teljega vastavalt -teljega vastavalt 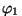 ja ja
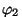 . .
Et neid võnkumisi liita, tuleb liita faasidiagrammid
(milline kohmakas väljend phasoriga võrreldes!).
Liitnud vektorid rööpkülikureegli abil, näeme, et summaarse
võnkumise amplituud ja algfaas erinevad lähtevõnkumiste omast.
Lahutame liidetavad komponentideks, liidame need ja saame
tingimused, mis määravad otsitavad suurused:
|
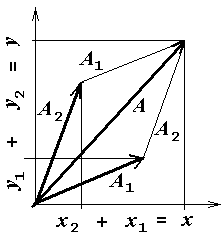
Phasor'ite liitmine. Võime kasutada nii koordinaatmeetodit kui rööpkülikureeglit.
|
Pärast trigonomeetrilisi teisendusi saame
See, koosinuslauset meenutav valem kannab nime amplituudide
reegel ja on lainefüüsika kõige tähtsam valem.
3.
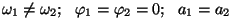
Võtsime esialgu amplituudid võrdseks, et kasutada trigonomeetriat. Saame:
|
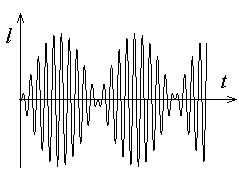
Tuiklemine.
Liitvõnkumise amplituud muutub harmoonilise liikumise seduse kohaselt.
|
Nurksulgudes olevat avaldist võime vaadelda kui ajas
muutuvat amplituudi.
Kui
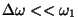 , saame nn.
tuiklemise, kus võnkumine toimub peaaegu vana sagedusega,
amplituud aga kõigub sagedusega , saame nn.
tuiklemise, kus võnkumine toimub peaaegu vana sagedusega,
amplituud aga kõigub sagedusega
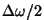 . .
Lihtne on ka
siis, kui sagedused väga kõvasti erinevad - siis toimub ühe
(väikese sagedusega) võnkumise taustal kiire (suurema
sagedusega) virvendus.
Kõige keerulisem on muidugi suvaliste
sageduste juhtum - siis ei jää tõesti üle midagi muud, kui
liita valemid.
Ülalöeldu kõlbab ka siis, kui amplituudid ei ole võrdsed. Pilt
jääb (peaaegu) samaks, ainult et minimaalne amplituud pole enam
null, vaid komponentide amplituudide vahe.
Küsimus: Et kirjeldatud liikumised pole harmoonilised, on selge. Aga kas nad on perioodilised? Kui jah, siis milline on periood?
|
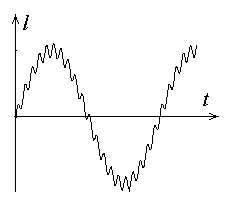
Virvendus.
Kiire "värin" aeglasema võnkumise taustal.
|
|
B. Ristsuunalised võnkumised. Kui liidame kaks
harmoonilist võnkumist, saame tasandilise kõvera, mis
sõltuvalt komponentide sagedustest võib olla suletud
kõver, kui sageduste suhe on ratsionaalarv ning lahtine
kõver, kui suhe on irratsionaalne (vähemalt üks komponentidest
on irratsionaalarv).
Neist esimese kuju sõltub komponentide
sagedustest ja faasivahest; teda nimetatakse Lissajous'
kujundiks, mille lihtsamad variandid on hästi uuritud. Kõik
summaarsed kõverad mahuvad ristkülikusse mõõdetega
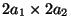 ; lahtine kõver täidab pikapeale kogu selle pindala. ; lahtine kõver täidab pikapeale kogu selle pindala.
Kui on tegemist kolme omavahel ristuva võnkumisega, tekib
ruumiline kõver risttahukas
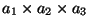 .
Põhimõtteliselt võib seegi olla kinnine või lahtine joon. .
Põhimõtteliselt võib seegi olla kinnine või lahtine joon.
Missugune kujund tekib aga nelja või rohkema võnkumise liitmisel?
|
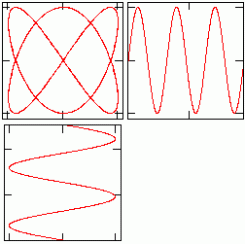
Lissajous' kujund perioodide suhtega 2:3 -- komponendid ja summa.
|
Võnkumiste energia. Et võnkuv keha on liikumises,
saame arvutada tema kiiruse ja kiirenduse, diferentseerides
võnkumiste võrrandit aja järgi. Nii saame:
Näeme, et kiirus ja kiirendus muutuvad sama seaduspärasuse
järgi, ennetades hälvet faasis vastavalt veerand perioodi
(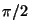 ) ning poole perioodi ( ) ning poole perioodi (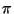 ) võrra. Seega on võnkuva
keha kiirus maksimaalne hetkel, kui hälve on null, kiirendus aga
maksimaalse hälbe momendil. ) võrra. Seega on võnkuva
keha kiirus maksimaalne hetkel, kui hälve on null, kiirendus aga
maksimaalse hälbe momendil.
|
|
Keha energia leiame
kineetilise ja potentsiaalse energia summana. Meie näites on
potentsiaalseks energiaks elastsusjõu energia 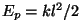 ning ning
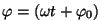 on faas.
Arvestades, et on faas.
Arvestades, et
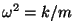 , saame , saame
|
Võnkuva keha energia on võrdeline
- keha massiga;
- amplituudi ruuduga;
- sageduse ruuduga.
|
|
Sama tulemuse saame, leides kineetilise või potentsiaalse
energia maksimaalväärtuse vastavalt tasakaaluasendis ning
maksimaalse hälbe momendil.
Seega toimub võnkumise ajal pidevalt
kineetilise energia üleminek potentsiaalseks ja vastupidi.
Koguenergia seejuures ei muutu; seepärast nimetatakse
harmoonilisi võnkeid ka sumbumatuteks võnkumisteks.
Et tegelikkuses toimub alati energiakadu hõõrdumise või
õhutakistuse tõttu, on vabavõnked idealisatsioon. Harmooniliste
võnkumiste näiteks on lisaks võnkumistele elastsusjõu mõjul veel
vedeliku võnked 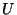 -torus, kuulikese veeremine paraboolsel
pinnal ning (ligikaudselt!) ka pendli väikese amplituudiga
võnked. -torus, kuulikese veeremine paraboolsel
pinnal ning (ligikaudselt!) ka pendli väikese amplituudiga
võnked.
|
|
Sumbuvvõnked.
Takistav jõud. Et kirjeldada reaalseid võnkeprotsesse,
tuleb liikumisvõrrandisse viia liige, mis väljendaks võnkumist
takistavat jõudu. Selle liikme kirjapanekul arvestame, et
- takistav jõud mõjub ainult liikuvale kehale;
- jõud takistab liikumist, st. mõjub liikumise vastassuunas;
- jõud on dissipatiivne, st. vähendab süsteemi energiat.
|
Kui võnkumiste energia kahaneb, tekivad sumbuvvõnked.
|
|
Meie poolt õpitutest kõlbavad seega hõõrde- ja takistusjõud.
Matemaatiliselt lihtsam on kasutada väikestel kiirustel
kehtivat keskkonnatakistust (sisehõõrdejõudu):
kus 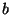 on takistustegur ja on takistustegur ja 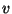 võnkuva keha kiirus. võnkuva keha kiirus.
Lisades selle vabavõngete võrrandile, saame:
Asendades kiiruse ja kiirenduse tuletistega ning viies nad
teisele poole võrdusmärki, saamegi sumbuvvõngete võrrandi:
|
Takistavas keskkonnas on võnkuva keha liikumisvõrrandiks
lineaarne
homogeenne
II järku
diferentsiaalvõrrand.
|
|
Matemaatikute jaoks on see lineaarne homogeenne II järku
diferentsiaalvõrrand, mille lahendi saab avaldada sama astme
polünoomi, nn. karakteristliku võrrandi
juurte
kaudu.
Diferentsiaalvõrrandi lahendi tüüp sõltub nüüd juurte
tüübist:
- Kui need on reaalarvud (st. ruutjuure alune
avaldis on positiivne), on otsitavaks funktsiooniks
(üldlahendiks) eksponentfunktsioon:
millele vastab hääbuv liikumine.
- Negatiivne juurealune avaldis
viib kompleksarvuliste juurte juurde:
|
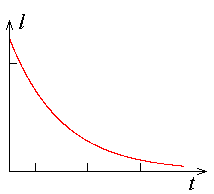
Hääbuv liikumine:
kaugus tasakaaluasendist kahaneb eksponentfunktsiooni kohaselt.
|
kus
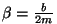 on reaal- ja on reaal- ja
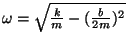 imaginaarosa.
Üldlahendiks on nüüd imaginaarosa.
Üldlahendiks on nüüd
mis sisaldab üheaegselt nii hääbuvat kui perioodilidelt muutuvat
osa.
- Lihtsaimat lahendit
kus 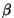 ja ja 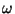 omavad ülaltoodud tähendust, nimetame
sumbuvateks võnkumisteks ja neid võib ligikaudselt
vaadelda kui eksponentsiaalselt kahaneva amplituudiga
harmoonilisi võnkumisi. omavad ülaltoodud tähendust, nimetame
sumbuvateks võnkumisteks ja neid võib ligikaudselt
vaadelda kui eksponentsiaalselt kahaneva amplituudiga
harmoonilisi võnkumisi.
|
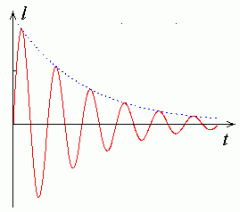
Eksponentsiaalselt kahaneva amplituudiga ("peaaegu harmoonilised") võnked.
|
Seda, et toodud valem lähtevõrrandit
rahuldab, saab igaüks kontrollida, võttes temast I ja II järku
tuletised ning asendades need lähtevõrrandisse.
Suurusi 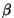 ja ja 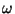 nim. vastavalt sumbuvate võnkumiste
sumbuvusteguriks ja omasageduseks. nim. vastavalt sumbuvate võnkumiste
sumbuvusteguriks ja omasageduseks.
Võttes arvesse, et
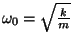 oli meie süsteemi vabavõngete sagedus e.
süsteemi omavõnkesagedus, võime sumbuvate võngete sageduse
avaldada kujul: oli meie süsteemi vabavõngete sagedus e.
süsteemi omavõnkesagedus, võime sumbuvate võngete sageduse
avaldada kujul:
Loomulikult kehtib see valem vaid juhul, kui
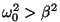 . Vastasel korral on meil karakteristliku
võrrandi dekrement (juurealune avaldis lahendi valemis)
positiivne ning võnkuv lahend puudub. . Vastasel korral on meil karakteristliku
võrrandi dekrement (juurealune avaldis lahendi valemis)
positiivne ning võnkuv lahend puudub.
Veel märgime, et
sumbuvvõngete omavõnkeperiood
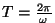 on seda
suurem, mida suurem on sumbuvustegur. Piirjuhul on seda
suurem, mida suurem on sumbuvustegur. Piirjuhul
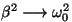
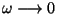 ehk ehk
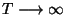 muutub liikumine
aperioodiliseks (st. mitteperioodiliseks). muutub liikumine
aperioodiliseks (st. mitteperioodiliseks).
|
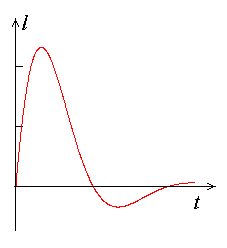
"Vahepealne variant" -- aperioodiline liikumine.
|
Energiakadu võngete sumbumisel. Sumbuvuse dekrement.
Kui sumbuvustegur 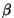 on väike, langeb sumbuvvõngete sagedus
praktiliselt ühte omavõnkesagedusega. Seetõttu neid tihtipeale
ei eristata, käsitledes sumbuvvõnkeid kui väheneva amplituudiga
vabavõnkumisi.
Et vabavõngete energia oli võrdeline amplituudi on väike, langeb sumbuvvõngete sagedus
praktiliselt ühte omavõnkesagedusega. Seetõttu neid tihtipeale
ei eristata, käsitledes sumbuvvõnkeid kui väheneva amplituudiga
vabavõnkumisi.
Et vabavõngete energia oli võrdeline amplituudi
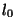 ruuduga, väheneb võnkuva keha energia iga täisvõnkega ruuduga, väheneb võnkuva keha energia iga täisvõnkega
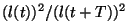 korda.
Suhet korda.
Suhet 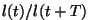 nimetame sumbuvuse
dekremendiks (ld. decrementum=kahanemine).
Lihtne arvutus
näitab, et dekrement võrdub nimetame sumbuvuse
dekremendiks (ld. decrementum=kahanemine).
Lihtne arvutus
näitab, et dekrement võrdub 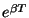 -ga. -ga.
|
Amplituudi (energia) vähenemist võnkumise käigus kirjeldab sumbuvuse dekrement.
|
Sagedamini
kasutatakse logaritmilist dekrementi
Energia kahaneb seega iga võnkega 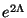 korda. korda.
Autovõnked. Selleks, et hoida mehaanilist (või mõnda
muud) süsteemi võnkumises, tuleb tema energiavaru regulaarselt
täiendada. Juhul, kui lisaenergia allikat lülitab sisse võnkuv
süsteem ise, on tegemist autovõngetega.
Autovõnkumiste näiteks on kõik mehaanilised kellad. Oluline on
see, et pendel (balansiir) saab energiat kellapommilt või
vedrult sama perioodiga, millega süsteem võngub.
Autovõnked kujutavad seega sumbumatuid võnkumisi, mille
võnkeperiood siiski pisut erineb omavõnkeperioodist
(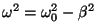 ). ).
Sundvõnked seevastu toimuvad
alati välise teguri (energiaallika) poolt määratud sagedusega,
mis ainult erijuhul võib kokku langeda omavõnkesagedusega.
|
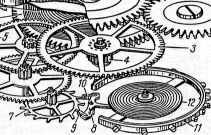
Autovõngete tavanäide - kellamehhanism.
Iga võnke järel annab kellavedru poolt veetav hammasratas (7) balansiirile (11) tõuke, mis kompenseerib hõõrdumisel kaotsi läinud energia.
|
|
Elektrivõnked
Kujutame ette, et juhtivas keskkonnas (näiteks traadijupis) on
tekitatud laengute polarisatsioon, mistõttu juhtme üks ots
onlaetud positiivselt, teine aga negatiivselt. Selle tulemusel
on juhis elektrivälja tugevus 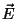 nullist erinev, mistõttu
tekib laengute liikumine - elektrivool. Et voolga kaasneb
magnetväli, mis muutudes kutsub omakorda esile induktsiooni
elektromotoorjõu, mõjub juhis liikuvale laengule kaks
vastassuunalist jõudu, millest üks (elektriväli) püüab
suurendada laengute liikumiskiirust (voolutugevust), teine
(eneseinduktsiooni EMJ) aga takistab seda.
Pilt on analoogiline
masspunkti liikumisega jõuväljas, kus väline jõud nullist erinev, mistõttu
tekib laengute liikumine - elektrivool. Et voolga kaasneb
magnetväli, mis muutudes kutsub omakorda esile induktsiooni
elektromotoorjõu, mõjub juhis liikuvale laengule kaks
vastassuunalist jõudu, millest üks (elektriväli) püüab
suurendada laengute liikumiskiirust (voolutugevust), teine
(eneseinduktsiooni EMJ) aga takistab seda.
Pilt on analoogiline
masspunkti liikumisega jõuväljas, kus väline jõud 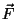 kiirendab
punkti liikumist, inertsijõud kiirendab
punkti liikumist, inertsijõud
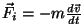 aga
takistab seda. aga
takistab seda.
|
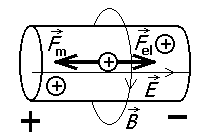
Võnkuvad laengud sirgjuhtmes.
|
Elektriskeemidel kujutatakse seda tavaliselt nn.
võnkeringina, mis koosneb induktiivsusest 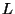 ning
mahtuvusest ning
mahtuvusest 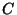 .
Loomulikult on igal juhil nii mahtuvus
(väljendab potentsiaali muutust laengu lisamisel) kui ka
induktiivsus (väljendab eneseinduktsiooni elektromotoorjõudu
voolutugevuse muutmisel), tähised on vajalikud nende omaduste
fikseerimiseks. .
Loomulikult on igal juhil nii mahtuvus
(väljendab potentsiaali muutust laengu lisamisel) kui ka
induktiivsus (väljendab eneseinduktsiooni elektromotoorjõudu
voolutugevuse muutmisel), tähised on vajalikud nende omaduste
fikseerimiseks.
Et kirja panna valemeid, mis
kirjeldaksid laengute liikumist, alustame Kirchoff'i II
reeglist. Kuna tegu on ühe ringiga, tuleb ka üks valem:
|
|
Asendades siia 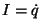 ning jagades mõlemaid pooli ning jagades mõlemaid pooli 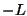 -ga, saame -ga, saame
mille lahendiks on vabavõngete võrrand
|
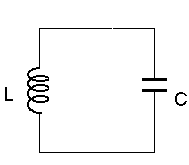
Võnkering.
|
milles
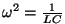 on võnkeringi omavõnkesagedus. on võnkeringi omavõnkesagedus.
Füüsikaline sisu: kondensaatori tühjenemisel kasvab voolutugevus
koos laengu vähenemisega ning saavutab maksimaalväärtuse hetkel,
kus laeng on null ja elektriväli juhis puudub. Samaks hetkeks
omandab maksimaalse tugevuse ka juhet ümbritsev magnetväli 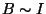 . Pinge kondensaatoril on nüüd null, samuti võrdub
nulliga ka elektriväli. Vool juhtmes aga ei katke, kuna nõrgenev
magnetväli tekitab omakorda indutseeritud elektrivälja, mis,
sundides laenguid liikumist jätkama, laeb kondensaatori uuesti
- seekord aga vastasmärgiliselt. Laadimisvool lakkab alles
siis, kui kondensaatori elektriväli peatab laengute liikumise
juhtmes. Edasi kordub kõik uuesti, kuid ümberpööratud polaarsusega. . Pinge kondensaatoril on nüüd null, samuti võrdub
nulliga ka elektriväli. Vool juhtmes aga ei katke, kuna nõrgenev
magnetväli tekitab omakorda indutseeritud elektrivälja, mis,
sundides laenguid liikumist jätkama, laeb kondensaatori uuesti
- seekord aga vastasmärgiliselt. Laadimisvool lakkab alles
siis, kui kondensaatori elektriväli peatab laengute liikumise
juhtmes. Edasi kordub kõik uuesti, kuid ümberpööratud polaarsusega.
Märgiprobleemist. Pinge kondensaatoril
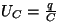 ,
genereerides voolu suunaga plussilt miinusele, tekitab
vastassuunalise induktsiooni EMJ ,
genereerides voolu suunaga plussilt miinusele, tekitab
vastassuunalise induktsiooni EMJ
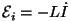 . Et
laengule mõjuvad nad üheaegselt, peaks summaarne pinge juhtmes
võrduma . Et
laengule mõjuvad nad üheaegselt, peaks summaarne pinge juhtmes
võrduma
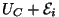 ehk ehk
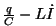 , mis erineb
Kirchoffi reeglist saadud valemist. , mis erineb
Kirchoffi reeglist saadud valemist.
Märgiviga tekib
kondensaatori juures: me ei arvestanud voolu suunaga. Pinge
kondensaatoril on küll suunatud plussilt miinusele, aga
vool vooluringis kulgeb piki juhtmeid, mitte aga "otse". Kui
joonistada voolu suund "üle kondensaatori" (vt. joonis), näeme,
et see läheb miinuselt plussile.
Seega vastaks meie skeemile pingelang
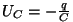 , mis
"neutraliseerib" , mis
"neutraliseerib" 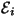 miinusmärgi. miinusmärgi.
|
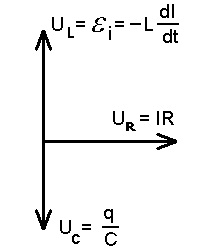
Elektrivõnkumiste faasidiagramm.
Induktsiooni elektromotoorjõud on alati vastassuunaline pingega kondensaatoril, voolutugevuse faasinurk jääb täpselt nende vahele ("vektor" IR on kaksiknoolega ULUC risti).
|
Pinge (potentsiaalide vahe) märk on üldse üks salakaval asi.
Märgi valikul tuleb alati vaadata, kas pinge muutus suurendab
või vähendab kondensaatori energiat.
Meie juhul energia vähenes,
järelikult pidi pingelangu märk olema negatiivne. Pärast seda,
kui kondensaator oli tühjenenud ja algas uus laadimine,
pingelangu märk muutus. Et aga samast momendist alates
voolutugevus mitte enam ei kasva, vaid kahaneb, muutub ka
elektromotoorjõu märk ning märgid tasakaaluvõrrandis jäävad samaks.
Sumbuvad elektrivõnked. Reaalses vooluahelas on alati
ka nn. oomiline takisti, kus pingelang tekib
elektrienergia muutumisest soojuseks (Joule-Lenz'i seadus).
Sellise ahela kohta annab Kirchoff'i reegel
millele vastab juba tuntud homogeenne diferentsiaalvõrrand
lahendiga
kus
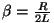 ning ning
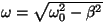 . .
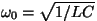 oli mäletatavasti omavõnkesagedus. oli mäletatavasti omavõnkesagedus.
|
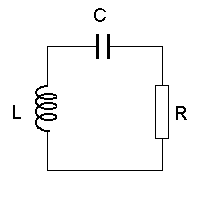
"Reaalne vooluring" koosneb mahtuvusest (kondensaatorist) C, induktiivsusest L ja oomilisest takistist R. Sellises võnkeringis tekivad sumbuvad elektrivõnked.
|
![]() Harmooniline liikumine
Harmooniline liikumine ![]() Tasakaalu tingimused
Tasakaalu tingimused ![]() Potentsiaalse energia miinimumi lause
Potentsiaalse energia miinimumi lause ![]() Direktsioonijõud
Direktsioonijõud ![]() Vabavõnked ja harmoonilised võnked
Vabavõnked ja harmoonilised võnked ![]() Siinusvõnked
Siinusvõnked ![]() Võnkumist iseloomustavad suurused
Võnkumist iseloomustavad suurused ![]() Ajas muutumatud
Ajas muutumatud ![]() Ajas muutuvad
Ajas muutuvad ![]() Faasidiagramm ja võnkumiste liitmine
Faasidiagramm ja võnkumiste liitmine ![]() Samasihilised võnkumised
Samasihilised võnkumised ![]() Faasidiagramm
Faasidiagramm ![]() Amplituudide reegel
Amplituudide reegel ![]() Tuiklemine
Tuiklemine ![]() Ristsuunalised võnkumised
Ristsuunalised võnkumised ![]() Lissajous' kujundid
Lissajous' kujundid ![]() Võnkumiste energia
Võnkumiste energia ![]() Sumbuvvõnked
Sumbuvvõnked ![]() Sumbuvvõngete võrrand
Sumbuvvõngete võrrand ![]() Sumbuvustegur
Sumbuvustegur ![]() Sumbuvuse dekrement
Sumbuvuse dekrement ![]() Autovõnked
Autovõnked ![]() Elektrivõnked
Elektrivõnked ![]() Võnkering
Võnkering ![]()