TÄIENDUSEKS  VEA-ARVUTUSELE

 

 

1. Mõõtemääramatuse kirjapanekust.

 

Metroloogia – teadus mõõtmistest – lähtub eeldusest, et mõõdetava suuruse tegelikku väärtust on võimalik kindlaks määrata vaid teatud piirini. Seda “absoluutsest tõest” puudujäävat osa on hakatud nimetama mõõtemääramatuseks (ingl. measurement uncertainity).

 

Tavakeeles kasutame sõnu “mõõteviga” ja “mõõtetäpsus”. Esimene tähistab mõõdetud suuruse tegeliku väärtuse erinevust mõõtetulemusest (mõõtarvust), teine iseloomustab vea suurust võrreldes mõõtetulemuse endaga. Nende matemaatilisteks väljendajateks on absoluutne piirviga ning suhteline (kasutatakse ka võõrkeelset väljendit “relatiivne”) viga. Tavatähiseid kasutades: kui x on mõõdetav suurus, siis

 

            x on mõõteviga (absoluutne piirviga) ja

            x/x  on mõõtetäpsus (suhteline viga)

 

Tulemust oleme harjunud kirjutama kujul  x ± x, millega väidetakse,et  x  tegelik väärtus asub kusagil  (x – x)  ja   (x + x)  vahel.

 

Rääkides määramatusest tahetakse öelda, et kuna me tõelist väärtust ei tea, ei tea me ka viga. Ehk teiste sõnadega – vea kirjapanek tähendaks seda, et me teame, kui palju me eksisime.

 

Mõõtemääramatust hinnatakse statistiliselt – analüüsides mõõtmiste seeriat mingist varemvalitud hüpoteesist lähtuvalt. Tulemuseks saadakse väärtuste vahemik, kuhu mõõdetava suuruse tegelik väärtus teatud tõenäosusega langeb. Seda tõenäosust nimetatakse usaldusnivooks (confidence level).

 

Kirjapaneku seisukohalt pole mingit vahet: ka määramatus pannakse kirja absoluutse piirvea kujul.

 

 

2. Arvutused vigaste suurustega.

 

Vea ülekandmisel arvutust käigus kasutame ainult täisdiferentsiaali valemit.

 

Olgu funktsioon antud võrrandiga

 

F = f(x,y,z,…) ; suurused x, y, z  vastavalt piirvigadega  x , y , z . Suuruse F piirviga  F  leitakse valemiga:

 

F =|f’_x|x + |f’_y|y + |f’_z|z .

 

kus  f’_x  tähistab funktsiooni  f  tuletist  x  järgi (matemaatikute keelepruugis nimetatakse seda osatuletiseks). Osatuletise võtmine mitme muutuja funktsioonist ei erine millegi poolest tavalise ühe muutuja funktsiooni tuletise võtmisest, teisi muutujaid (y , z) käsitletakse selle juures kui konstante.

 

Näide:  F = x² + y² + xy + z

 

            F’_x = ( x² )’_x + ( y² )’_x + ( xy)’_x + (z)’_x  = 2x + 0 + y + 0 = 2x + y

 

Vea valemiks saame:

 

            F =|f’_x|x + |f’_y|y + |f’_z|z = (2x + y) x + (2y + x) y + z .

 

NB!  Absoluutväärtuse märgid tuletiste juures on olulised! Kuna kõik vead antakse märgiga  ± , siis piirvea (tähendab maksimaalset võimalikku viga) leidmisel tuleb vead igal juhul liita, vaatamata sellele, millise märgiga on tuletis.

 

Harjutuseks: Lähtudes täisdiferentsiaali valemist, tuletage kahe “vigase arvu” summa, vahe ja korrutise vea valemid.

 

3. Lihtsustavaid nippe.

 

Jagatis, astmefuktsioon, juured  Tuletise arvutamisel annavad kooliõpikud tihti põhjendamatult keerukaid valemeid. Näiteks võib tuua nn. “jagatise tuletise” ja “tuletise ruutjuurest”.

 

Tegelikult on need mõlemad astmefunktsioonid, astmefunktsiooni tuletis on aga üks lihtsamaid:

 

          ( xⁿ )’ = n x^(n-1)

 

Kui nüüd kirjutada  a/x asemel  ax^(-1)  ja  ­­ x  asemel   x ^œ = x^0.5, saame kohe tuletised

 

(ax^(-1) )’ = -(1) ax^(-2)  = - ax^(-2)  

 

(x^0.5 )’ =  0.5 x ^-0.5

 

Ja ka päris keerulisest avaldisest saab asja:

 

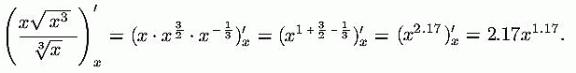
Elementaarfunktsioonid ja nende kombinatsioonid. Elementaarfunktsioonide tuletisi ise välja ei mõtle: need tuleb kas pähe õppida või leida käsiraamatust. Kombinatsioonide koha pealt on  kaks võimalust: kas kõnesolev funktsioon on osaks mingist algebralisest avaldisest või on algebraline avaldis funktsiooni argumendiks. Mõlemal juhul on tulemuseks korrutis: üheks teguriks tabelist leitud tuletis, teiseks teguriks kas ülejäänud osa avaldisest ( kui see on funktsiooni kordajaks) või siis tuletis nimetatud avaldisest (kui avaldis on elementaarfunktsiooni argumendiks).

 

Näide:

 

F = xy sin z :        F’_y = x sin z ;      F’_z = xy cos z ;     F’_x  = ?

 

F = x sin (yz) :   F’_x = sin (yz) ;   F’_y = x cos (yz) · z = xz cos (yz) ;  F’_z = ?

 

“Pikad read”. Nii nimetatakse tavaliselt algebralisi avaldisi, mis koosnevad vaheldumisi liitmis- ja korrutamistehetest, sisaldades ka astmeid, juuri ja elementaarfunktsioone. Siin ei aita muu, kui ülaltoodud lihtsate reeglite järjekindel rakendamine. Ja muidugi nõuab selline rehkendus püsivust ning tähelepanu.

 

Lõpliku pikkusega kümnendarvud.  Kalkulaatoriga rehkendamisel (ka “paberil korrutades”) saame alatihti arve, mis koosnevad kuuest kuni kümnest numbrikohast. Mida nendega peale hakata? Kui palju ümardada?

 

Siingi aitab täisdiferentsiaali valem. Olgu meil näiteks korrutis:

 

            17,76 · 78,3 = 1390,608

 

Seitse numbrikohta on siin kindlasti kurjast. Aga kui palju on õige?

 

Lähtume eeldusest, et teguriteks on ümardatud arvud. Esimene neist ei saa olla suurem kui 17,765 ega väiksem kui 17,755 . Määramatus on seega  ± 0.005 . Sama loogikaga saame teise teguri veaks  ± 0,05 .

 

Rakendame täisdiferentsiaali valemit.

 

( a · b ) = a · b + b · a  = 17,76 · 0,05 + 78,3 · 0,005 = 1,2795

 

Viga ümardatakse antud juhul kahe numbrikohani  ( 1,3 ) ,  tulemus antakse sama arvu kümnendkohtadega. Korrektne vastus oleks:

 

17,76 · 78,3 = 1390,6 ± 1,3

 

ehk, kui viga mitte kirjutada, 1390,6 – üks number rohkem kui kõige pikemal teguril.

 

Kas olete sellist reeglit varem kohanud?

Kas oskate seda nüüd ka matemaatiliselt tõestada?