Loeng 9. Molekulaarfüüsika: erisoojused ja ülekandenähtused
Olekuvõrrandi mehhanistlik esitus. 1811. a.
formuleeris itaalia füüsik Amedeo Avogadro moolruumalade võrdsuse
seaduse, mida tänapäeval tunneme Avogadro seadusena:
Samadel füüsikalistel tingimustel on kõigi gaaside
moolruumalad võrdsed.
Sisuliselt on see olekuvõrrandi üks võimalik sõnastus ja vaevalt
oleks ta erilist tähelepanu esile kutsunud, kui mitte Avogadro
ise poleks andnud talle huvitava tõlgenduse:
et kõigi ainete
gramm-molekulid sisaldavad võrdse arvu osakesi (molekule), siis
sõltub molekulide ruumtihedus üksnes rõhust ja temperatuurist.
Asendades olekuvõrrandis ainehulga 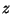 molekulide arvuga molekulide arvuga
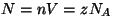 (suurust (suurust 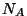 , mis väljendab molekulide arvu ühes
moolis aines, nim. Avogadro arvuks), saame , mis väljendab molekulide arvu ühes
moolis aines, nim. Avogadro arvuks), saame
|
Avogadro seadus on samaväärne Clapeyroni võrrandiga.
|
kus
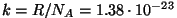 J/K kannab nimetust Boltzmanni konstant. J/K kannab nimetust Boltzmanni konstant.
|
Boltzmanni konstanti võib vaadelda kui "vaba molekuli universaalkonstanti".
|
Olekuvõrrandi kaks kuju erinevad selle poolest, et esimene neist
(Clapeyroni-Mendelejevi võrrand) on puht-empiiriline, sidudes otseselt
mõõdetavaid suurusi. Teine seevastu lähtub aine diskreetsuse
hüpoteesist (kõik ained koosnevad molekulidest). Hüpoteesi
kinnituseks pidi olema Avogadro arvu katseline määramine, mis
õnnestus alles sadakond aastat hiljem (Jean Perrin, 1909, lähtudes
Browni liikumisest). Küll aga võimaldas teine kuju üles ehitada
termodünaamika mehhanistliku esituse - gaaside
molekulaar-kineetilise teooria.
Molekulaar-kineetilise teooria põhivõrrand tuletatakse
eeldusest, et gaasi rõhk tekib molekulide põrgetel vastu anuma
seina (gaasi või vedeliku sisse paigutatud keha välispinda). Et
impulssesituses avaldub Newtoni II seadus kujul
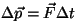 , võime rõhu avaldise kirjutada
kus , võime rõhu avaldise kirjutada
kus
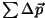 on kõigi ajavahemiku on kõigi ajavahemiku 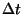 jooksul vastu
pinnatükki jooksul vastu
pinnatükki 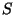 põrganud molekulide summaarne impulsimuutus.
(Õnnetuseks tähistatakse nii impulssi kui rõhku põrganud molekulide summaarne impulsimuutus.
(Õnnetuseks tähistatakse nii impulssi kui rõhku
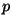 -ga, seetõttu eristab neid meie valemites vaid vektorimärk.)
Impulsi muutust on lihtne arvutada, kui teame impulssvektori
suunda ja suurust enne põrget; paraku pole mingit lootust seda
kõigi molekulide kohta teada saada.
Siin tulebki mängu statistika. Me teeme oletuse, et gaas
koosneb molekulidest; kujutame neid punktmassidena ja rakendame neile
Newtoni seadusi. Saadud tulemusi töötleme statistika valemite abil
ning leiame meid huvitava suuruse kui üksikute molekulide
parameetrite keskväärtuse. -ga, seetõttu eristab neid meie valemites vaid vektorimärk.)
Impulsi muutust on lihtne arvutada, kui teame impulssvektori
suunda ja suurust enne põrget; paraku pole mingit lootust seda
kõigi molekulide kohta teada saada.
Siin tulebki mängu statistika. Me teeme oletuse, et gaas
koosneb molekulidest; kujutame neid punktmassidena ja rakendame neile
Newtoni seadusi. Saadud tulemusi töötleme statistika valemite abil
ning leiame meid huvitava suuruse kui üksikute molekulide
parameetrite keskväärtuse.
Teeme näiteks oletuse, et kõik molekulid liiguvad võrdsete
kiirustega ja pind 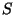 , millele mõjuvat rõhku arvutame, asub , millele mõjuvat rõhku arvutame, asub
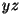 -tasandis. Põrgete arvu rehkendame molekulide ruumtiheduse -tasandis. Põrgete arvu rehkendame molekulide ruumtiheduse 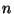 (molekulide arv kuupmeetris) ja liikumiskiiruse
(molekulide arv kuupmeetris) ja liikumiskiiruse 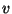 abil. Kui molekulid liiguksid kõik abil. Kui molekulid liiguksid kõik 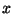 -telje ehk baasivektori -telje ehk baasivektori 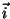 suunas, jõuaks meie pinnatükini ajavahemiku
suunas, jõuaks meie pinnatükini ajavahemiku 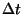 jooksul jooksul
|
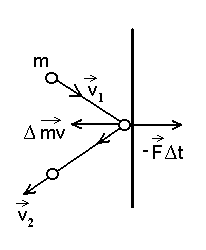
Ühe molekuli põrkel seinale antud (jõu)impulss.
Kuna me ei tea põrke kestust, siis mingit "seinale mõjuvat jõudu" me sellest arvutada ei saa.
|
molekuli. Kui lugeda põrge seinaga absoluutselt elastseks, hakkaksid
molekulid pärast põrget liikuma vastassuunas ja sama kiirusega --
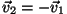 , seega muutuks nende impulss , seega muutuks nende impulss
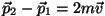 võrra. Pinnatükile võrra. Pinnatükile  mõjuva rõhu valemis asendame mõjuva rõhu valemis asendame
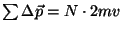 ja saame rõhu ja saame rõhu 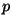 väärtuseks
Paraku ei anna see valem meile otsitavat rõhku. Molekulaarfüüsika
üheks eelduseks, mida kinnitab toosama Browni liikumine, on see, et
molekulid liiguvad kaootiliselt, st kõikvõimalikes suundades ja
kõikvõimalike kiirustega. Et leida õiget rõhku, tuleb meil arvutada
keskväärtus. väärtuseks
Paraku ei anna see valem meile otsitavat rõhku. Molekulaarfüüsika
üheks eelduseks, mida kinnitab toosama Browni liikumine, on see, et
molekulid liiguvad kaootiliselt, st kõikvõimalikes suundades ja
kõikvõimalike kiirustega. Et leida õiget rõhku, tuleb meil arvutada
keskväärtus.
Teeme asja pisut lihtsamaks, oletades, et gaas koosneb
ühesugustest molekulidest.
Ja nüüd statistika:
- Pinnatüki
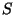 poole liiguvad pooled molekulid - jagame
leitud rõhu kahega; poole liiguvad pooled molekulid - jagame
leitud rõhu kahega;
- Iga kiiruse ruut avaldub kolme komponendi
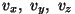 ruutude summana. Meile läheb korda vaid
ruutude summana. Meile läheb korda vaid 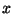 -komponent, mis on üks
kolmandik kolme komponendi ruutude summast - jagame tulemust veel
kolmega; -komponent, mis on üks
kolmandik kolme komponendi ruutude summast - jagame tulemust veel
kolmega;
- Asendame molekulide kiiruste ruutude summa nende
ruutkeskmise kiirusega
ja saame tulemuseks
|
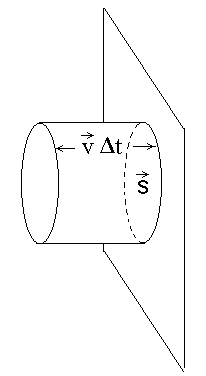 Molekulide "kollektiivne mõju".
Molekulide "kollektiivne mõju".
Ajavahemiku 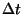 jooksul põrkuvad vastu silindri põhja (pindala S) kõik selles silindris olevad molekulid.
Gaasi rõhk on võrdeline molekulide ruutkeskmise kiirusega. jooksul põrkuvad vastu silindri põhja (pindala S) kõik selles silindris olevad molekulid.
Gaasi rõhk on võrdeline molekulide ruutkeskmise kiirusega.
|
Et valemis on rõhk võrdeline molekulide ruumtihedusega 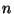 , saame
kohe lahti veel ühest piirangust. Me ei pea enam jälgima, et
molekulid oleks ühesugused. Kui meil on näiteks segu kolmest gaasist
tihedustega , saame
kohe lahti veel ühest piirangust. Me ei pea enam jälgima, et
molekulid oleks ühesugused. Kui meil on näiteks segu kolmest gaasist
tihedustega 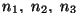 , saame kogurõhuks
Jälle hea valem: gaaside segu rõhk on võrdne komponentide osarõhkude
summaga. Pidage see meeles, võib tarvis minna.
Veelgi huvitavama seose saame, kui asendame , saame kogurõhuks
Jälle hea valem: gaaside segu rõhk on võrdne komponentide osarõhkude
summaga. Pidage see meeles, võib tarvis minna.
Veelgi huvitavama seose saame, kui asendame 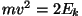 . Tuleb välja,
et . Tuleb välja,
et
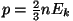 , ehk rõhk võrdub kahe kolmandikuga
molekulide kineetilisest energiast ruumiühiku kohta. Tõepoolest
-- ka dimensioon klapib: , ehk rõhk võrdub kahe kolmandikuga
molekulide kineetilisest energiast ruumiühiku kohta. Tõepoolest
-- ka dimensioon klapib:
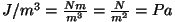 .
Asendame siia rõhu avaldise
molekulide ruumtiheduse ja temperatuuri kaudu: .
Asendame siia rõhu avaldise
molekulide ruumtiheduse ja temperatuuri kaudu:
|
Boltzmanni konstant seob molekulide keskmise kineetilise energia gaasi temperatuuriga.
|
|
-- molekuli kineetiline energia on võrdeline temperatuuriga!
Seega on molekulaar-kineetilises teoorias rõhk, energia ja
temperatuur ühe ja sellesama suuruse -- molekulide kiiruse --
avaldumisvormid. Siit ka teooria nimetus. Ilus teooria ja õige
kah - niivõrd, kuivõrd Newtoni mehaanikat saab rakendada nii
väikestele osakestele.
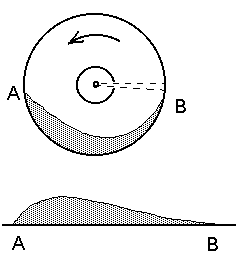
Gaasi soojusmahtuvus. Soojusmahtuvuse mõiste
tuleb mängu, kui uurime kehade soojenemist. Et tõsta mingi keha
temperatuuri ühe kraadi võrra, kulub kindel hulk soojust. See
ongi soojusmahtuvus.
Soojuse mõiste tuli füüsikasse koos temperatuuriga. Sedagi tuli
mõõta ning selleks defineeriti uus suurus -- soojushulk,
mille mõõtmiseks oli vaja ka ühikut. Algselt defineeriti
soojushulga ühik etaloonina: üks kalor (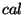 ) oli soojushulk,
mis tõstis ühe kuupsentimeetri vee temperatuuri ühe kraadi
võrra. Hiljem, kui inglise füüsik James Joule 1843. a. tõestas töö ja soojuse
ekvivalentsuse ( ) oli soojushulk,
mis tõstis ühe kuupsentimeetri vee temperatuuri ühe kraadi
võrra. Hiljem, kui inglise füüsik James Joule 1843. a. tõestas töö ja soojuse
ekvivalentsuse (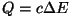 , , 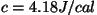 on soojuse
mehaaniline ekvivalent), hakati lihtsuse mõttes soojushulki
mõõtma energiaühikutes. Nii toimitakse ka SI-süsteemis;
"mehaanilist ekvivalenti" asendab mõiste "vee erisoojus": on soojuse
mehaaniline ekvivalent), hakati lihtsuse mõttes soojushulki
mõõtma energiaühikutes. Nii toimitakse ka SI-süsteemis;
"mehaanilist ekvivalenti" asendab mõiste "vee erisoojus":
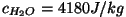 .
Anname nüüd definitsioonid: .
Anname nüüd definitsioonid:
-
Soojusmahtuvus
= soojushulk dzaulides, mis tõstab
keha temperatuuri ühe kelvini võrra
- Erisoojus
= soojushulk, mis tõstab antud aine
massiühiku (kilogrammi) temperatuuri 1 K võrra
- Moolsoojus
= soojushulk, mis tõstab antud aine ühe
mooli ...
|
Soojushulk ja energia on kattuvad mõisted; mõlemat võib mõõta sma ühikuga.
Keha soojusmahtuvus näitab, kui palju soojust (energiat) on vaja tema temperatuuri tõstmiseks ühe kelvini võrra.
Erisoojus ja moolsoojus iseloomustavad mitte kehi, vaid aineid.
|
Kui vedelikel ja tahketel ainetel piisab ühest erisoojusest,
siis gaaside soojusmahtuvus sõltub termodünaamilisest
protsessist. Isohoorilisel protsessil (konstantsel ruumalal)
kulub temperatuuri tõstmiseks vähem energiat, kui konstantse rõhu, seega muutuva
ruumala korral. Seetõttu eristatakse kaht mool- ja
erisoojust:
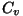 - isohooriline moolsoojus - kui soojendamine toimub
konstantse ruumala juures; - isohooriline moolsoojus - kui soojendamine toimub
konstantse ruumala juures;
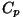 - isobaariline moolsoojus - kui soojendamine toimub
konstantsel rõhul. - isobaariline moolsoojus - kui soojendamine toimub
konstantsel rõhul.
Kui muutuvad nii rõhk kui ruumala, ei saa temperatuuri muutust
moolsoojuste abil arvutada. Siis lähtutakse olekuvõrrandist ja
protsessi valemitest.
Seose moolsoojuste väärtuste vahel leidis saksa arst Julius Mayer
1842. a., lähtudes eeldusest, et soojuste vahe kulutatakse
paisumisel tehtud tööks. Et paisumise töö isobaarilisel juhul on
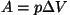 (
(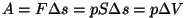 ), saame ühe
mooli gaasi jaoks olekuvõrrandist
millest järeldub
seos on tuntud Mayeri valemina.
Moolsoojused ise on erinevatel gaasidel üsna sarnased, sõltudes
vaid molekuli ehitusest.
Kõigil üheaatomilistel gaasidel
(inertgaasid näiteks) on ), saame ühe
mooli gaasi jaoks olekuvõrrandist
millest järeldub
seos on tuntud Mayeri valemina.
Moolsoojused ise on erinevatel gaasidel üsna sarnased, sõltudes
vaid molekuli ehitusest.
Kõigil üheaatomilistel gaasidel
(inertgaasid näiteks) on
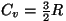 ,
kaheaatomilistel ,
kaheaatomilistel
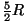 ,
kolme- ja enamaatomilistel ,
kolme- ja enamaatomilistel 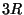 . .
Kavala tõestuse
on välja pakkunud molekulaarfüüsikud: et nende teoorias ühe
aatomi energia on
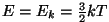 , saavad nad ühe mooli
koguenergiaks , saavad nad ühe mooli
koguenergiaks
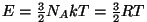 , kust , kust
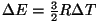 , millest , millest
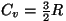 - nagu peabki
olema üheaatomilistel gaasidel. - nagu peabki
olema üheaatomilistel gaasidel.
Et kuidagi seletada
mitmeaatomiliste gaaside moolsoojusi, tuldi mõttele sisse tuua
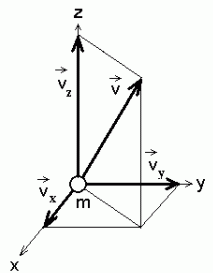
energia jagunemine vabadusastmete peale. Üheaatomilise
molekuli liikumisel on kolm vabadusastet (kiirusvektori kolm
komponenti), mitmeaatomilistel lisandub veel pöörlev liikumine
(nurkkiirusvektoril samuti kolm komponenti) - seega kokku kuus
vabadusastet.
Kuna energia salvestub kineetilise energiana
(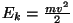 kulg- ja kulg- ja
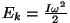 pöördliikumisel), sõltub salvestuva energia hulk lisaks kiiruse
ruudule ka massist (inertsimomendist). Energia valemisse kuuluv mass on kõigi
liikumissuundade jaoks ühesugune, inertsimoment seevastu sõltub
molekuli ehitusest. Kaheaatomilisel molekulil, kui aatomid lugeda
punktmassideks, on molekuli teljega (aatomeid ühendav sirglõik)
ühtiva telje suhtes inertsimoment null ja seetõttu ei kõlba üks
vabadusaste kuuest energia salvestamiseks - nii jääb
vabadusastmeid mitte kuus, vaid viis.
pöördliikumisel), sõltub salvestuva energia hulk lisaks kiiruse
ruudule ka massist (inertsimomendist). Energia valemisse kuuluv mass on kõigi
liikumissuundade jaoks ühesugune, inertsimoment seevastu sõltub
molekuli ehitusest. Kaheaatomilisel molekulil, kui aatomid lugeda
punktmassideks, on molekuli teljega (aatomeid ühendav sirglõik)
ühtiva telje suhtes inertsimoment null ja seetõttu ei kõlba üks
vabadusaste kuuest energia salvestamiseks - nii jääb
vabadusastmeid mitte kuus, vaid viis.
Moolsoojuse valemid võime seega
anda kujul:
- hea lihtne meeles pidada.
Aga kuidas arvutada erisoojusi?
|
Gaaside soojusmahtuvuse teoorias eristatakse kaht moolsoojust: isobaarilist ja isohoorilist. Neid seob Mayeri valem.
Molekuli kulgliikumise kineetilise energia seos vabadusastmetega: mv2=mvx2+mvy2+mvz2. Kui liita kokku kõigi molekulide energiad, tuleb iga vabadusastme kohta kolmandik summaarsest energiast.
Kaheaatomilise molekuli pöörlemisenergia.
Pöörlemine ümber z -telje energiat ei lisa, kuna inertsimoment on null.
|
|
Tasakaaluline kiiruste jaotus --
Maxwelli jaotus.
Kuna rõhk ja siseenergia avaldusid
keskmise kiiruse kaudu, peaks molekulaarfüüsika seisukohalt
olema lõpmatu arv kiiruste jaotusi, mis vastavad ühele ja
samale olekule (samale temperatuurile). Molekulaarfüüsikas väidetakse, et kõigist neist
võimalikest jaotustest on üks suurima tõenäosusega jaotus,
mida nimetatakse tasakaaluliseks jaotuseks. Molekulide
omavaheliste põrgete käigus toimub pidev energiavahetus, mille
tõttu muutuvad molekulide kiirused ja lõppkokkuvõttes ka
kiiruste jaotuse iseloom;
tasakaaluline jaotus on selline,
kus energiavahetused kiiruste jaotust ei muuda - mingist
kiiruste grupist
 põrgete tagajärjel
lahkuvate molekulide arv on võrdne sinna teistest gruppidest
tulevate molekulide arvuga. põrgete tagajärjel
lahkuvate molekulide arv on võrdne sinna teistest gruppidest
tulevate molekulide arvuga.
|
Molekulaarfüüsika seisukohalt on olek tasakaaluline siis, kui molekulide kiiruste jaotus enam ei muutu. Seda viimast nimetataksegi tasakaaluliseks jaotuseks.
|
|
Baromeetriline valem. Kõige lihtsam viis molekulide
kiiruste jaotuse määramiseks on uurida nende tiheduse jaotust
raskusjõu väljas. Siin on meil kasutada kaks valemit:
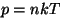 -- rõhu valem molekulaarfüüsikast, -- rõhu valem molekulaarfüüsikast,
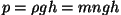 -- rõhu sõltuvus sügavusest
hüdrodünaamikas. -- rõhu sõltuvus sügavusest
hüdrodünaamikas.
Viimases valemis tuleb aga arvestada, et erinevalt vedelikest on
gaas kokkusurutav. Seetõttu sõltub tihedus rõhust ning meie
valemid on täpsed vaid lõpmata õhukeses kihis paksusega 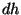 . .
Diferentseerime meie võrrandeid, saades
(miinusmärk näitab, et kõrguse suurenedes rõhk kahaneb).
Lahutame esimesest võrrandist teise, eraldame muutujad ning
integreerime:
kus 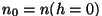 . .
Kui asendada selles valemis 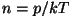 ja ja
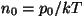 , saame baromeetrilise valemi, mis kirjeldabki
rõhu sõltuvust kõrgusest konstantse temperatuuri korral
(isotermilises atmosfääris). , saame baromeetrilise valemi, mis kirjeldabki
rõhu sõltuvust kõrgusest konstantse temperatuuri korral
(isotermilises atmosfääris).
|
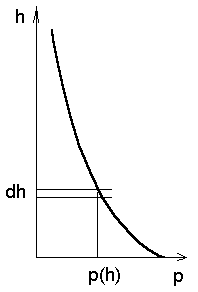
Baromeetrilise valemi tuletus: igas õhukeses kihis paksusega dh loeme rõhu ja tiheduse konstantseks; rõhk mingil kõrgusel h sisaldab kõigi kõrgemal olevate kihtide kaalude summat (integraali).
|
|
Küsimus: Kas suudate seda valemit siinsamas ja kohe kirja
panna?
Boltzmanni jaotus. Kui vaadata hoolega eksponendi 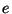 astendajat baromeetrilises valemis, näeme, et lugejas olev
suurus vastab massiga
astendajat baromeetrilises valemis, näeme, et lugejas olev
suurus vastab massiga 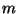 molekuli potentsiaalsele energiale
raskusjõu väljas. Kui lasta sellel molekulil kõrguselt molekuli potentsiaalsele energiale
raskusjõu väljas. Kui lasta sellel molekulil kõrguselt 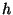 "alla
kukkuda", läheb tema potentsiaalne energia üle kineetiliseks: "alla
kukkuda", läheb tema potentsiaalne energia üle kineetiliseks:
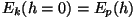 . Et molekulide jaotus atmosfääris peaks olema
tasakaaluline, saame kiiruste jaotuse kõrgusel . Et molekulide jaotus atmosfääris peaks olema
tasakaaluline, saame kiiruste jaotuse kõrgusel 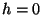 , kui
asendame baromeetrilises valemis potentsiaalse energia
kineetilisega ( , kui
asendame baromeetrilises valemis potentsiaalse energia
kineetilisega (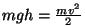 ): ):
|
Boltzmanni jaotuse saame, kui asendame baromeetrilises valemis potensiaalse energia mgh kineetilise energiaga mv2/2
|
Mida aga tähistab sel juhul suurus n?
Baromeetrilises valemis näitas see molekulide arvu ruumalaühiku
kohta kõrgusel 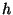 ,
kuid ei öelnud midagi nende molekulide kiiruste kohta. Võiksime
väita, et see tihedus sisaldab kõiki neid molekule, mis võiksid
tõusta kõrgemale kõrgusest ,
kuid ei öelnud midagi nende molekulide kiiruste kohta. Võiksime
väita, et see tihedus sisaldab kõiki neid molekule, mis võiksid
tõusta kõrgemale kõrgusest 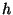 . Molekulide koguarv . Molekulide koguarv 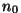 vastaks siis neile molekulidele, mis suudavad tõusta kõrgemale
kõrgusest
vastaks siis neile molekulidele, mis suudavad tõusta kõrgemale
kõrgusest 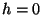 .
Kiiruste jaotuses väljendaks sel juhul arv .
Kiiruste jaotuses väljendaks sel juhul arv
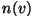 selliste molekulide ruumtihedust, mille kiirus on
suurem kiirusest selliste molekulide ruumtihedust, mille kiirus on
suurem kiirusest 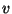 . Konstant . Konstant 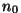 on nullist suurema kiirusega molekulide
arv ruumalaühikus ehk teiste sõnadega - molekulide kogutihedus.
Seda valemit nimetataksegi Boltzmanni jaotuseks.
Mikrofüüsikas väljendab ta kõige sagedamini osakeste jaotust energiate järgi.
Meie uurime praegu küll kiirusi - tegelikult on see aga ükspuha.
Boltzmanni jaotus kuulub nn.
integraalsete jaotusfunktsioonide hulka (statistikas nimetatakse
neid ka kumulatiivseteks - ld. cumulatio, kuhjumine). on nullist suurema kiirusega molekulide
arv ruumalaühikus ehk teiste sõnadega - molekulide kogutihedus.
Seda valemit nimetataksegi Boltzmanni jaotuseks.
Mikrofüüsikas väljendab ta kõige sagedamini osakeste jaotust energiate järgi.
Meie uurime praegu küll kiirusi - tegelikult on see aga ükspuha.
Boltzmanni jaotus kuulub nn.
integraalsete jaotusfunktsioonide hulka (statistikas nimetatakse
neid ka kumulatiivseteks - ld. cumulatio, kuhjumine).
Maxwelli jaotus seevastu on diferentsiaalne jaotusfunktsioon,
mis väljendab mingi kiirusega osakeste suhtelist hulka. Et
täpselt antud kiirusega liikuvate molekulide suhteline hulk on
lõpmata väike, defineeritakse diferentsiaalne jaotus valemiga
Meie juhul, kus kiiruse moodul ei saa olla negatiivne, on
nimetajas vahemik nullist lõpmatuseni. Integraalne
jaotusfunktsioon saadakse diferentsiaalse jaotusfunktsiooni integreerimisel
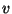 -st lõpmatuseni; aga võib ka integreerida suvalises
vahemikus, saades teatud kiiruste vahemikku kuuluvate molekulide
suhtelise hulga. -st lõpmatuseni; aga võib ka integreerida suvalises
vahemikus, saades teatud kiiruste vahemikku kuuluvate molekulide
suhtelise hulga.
Näiteks peab Maxwelli jaotusest tulenema
Boltzmanni jaotus:
Diferentsiaalse jaotusfunktsiooni leidmiseks tuleb lahendada
pöördülesanne: diferentseerides integraalset (Boltzmanni)
jaotust jõuda diferentsiaalse (Maxwelli) jaotuseni.
Lihtne
tuletise võtmine annab
mis pole paraku õige, kuna ei arvesta kiiruste jaotust suundade
järgi ega kogutiheduse sõltuvust temperatuurist.
Et ülesandega
hakkama saada, tuleb välja kannatada lühike geomeetriline
ekskursioon faasiruumi.
Kui kujutame kiiruste jaotust
faasiruumis, saame kolmemõõtmelise sfääri, kus kiiruste
vahemikule 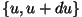 vastab kiht pindalaga vastab kiht pindalaga 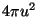 ning
paksusega ning
paksusega 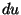 . Selle kihi ruumala vastabki vaadeldavasse
vahemikku langevate kiirustega osakeste suhtelisele hulgale. . Selle kihi ruumala vastabki vaadeldavasse
vahemikku langevate kiirustega osakeste suhtelisele hulgale.
Seega, kui kõik kiirused oleks võrdtõenäosed (faasiruum oleks
kiiruste osas ühtlaselt täidetud), saaksime
mis on täiesti absurdne oletus. Suure kiirusega osakeste arv
peab seetõttu kahanema kiiremini, kui 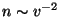 , ja see
saavutatakse eksponentteguri , ja see
saavutatakse eksponentteguri 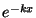 lisamisega valemisse. lisamisega valemisse.
|
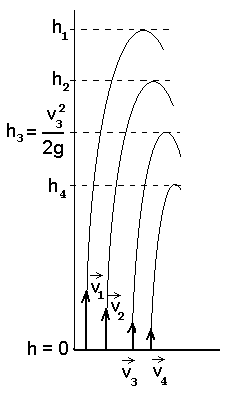
Kõrgusel h = 0 on kiirusest v suurema kiirusega molekule niisama palju, kui neid on kõrgemal kui h3= v32/2g .
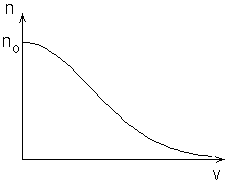
Boltzmanni jaotus kiiruste järgi.
Integraalne (kumulatiivne) jaotusfunktsioon näitab, kui palju on antud energiast suurema energiaga molekule.
Diferentsiaalne jaotusfunktsioon näitab, kui suur on mingisse kiiruste (kõrguste) vahemikku kuuluvate molekulide osakaal.
Mehaanikas nimetatakse faasiruumiks 6-mõõtmelist ruumi, mille koordinaatideks on lisaks tavalistele ruumikoordinaatidele
osakeste kiiruse või impulsi komponendid.
|
Tulemuseks on laialtkasutatav
valem
kus 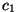 ja ja 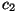 on
konstandid ning on
konstandid ning 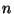 funktsiooni asümptoodile funktsiooni asümptoodile 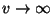 vastav
astendaja. Selle, astme- ja eksponentfunktsiooni korrutisena
saadava kõvera kujunemist illustreerib kõrvaltoodud graafik.
Meie ülesanne on konkreetsem: tuletada jaotusfunktsioon, mis on
ruumis isotroopne ja vastab Boltzmanni jaotusele. Kui liikumine
oleks ühemõõtmeline, võiksime joonisel kujutatud loogikast
lähtudes kirjutada diferentsiaalse jaotusfunktsiooni tuletisena:
Teguri vastav
astendaja. Selle, astme- ja eksponentfunktsiooni korrutisena
saadava kõvera kujunemist illustreerib kõrvaltoodud graafik.
Meie ülesanne on konkreetsem: tuletada jaotusfunktsioon, mis on
ruumis isotroopne ja vastab Boltzmanni jaotusele. Kui liikumine
oleks ühemõõtmeline, võiksime joonisel kujutatud loogikast
lähtudes kirjutada diferentsiaalse jaotusfunktsiooni tuletisena:
Teguri 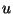 lisamine integraali on vajalik, kuna ühemõõtmelisel
juhul sõltub oskeste voog läbi "kontrollpinna" lisaks viimase
pindalale ka osakeste kiirusest: sama tiheduse korral jõuab
ajaühikus pinda läbida seda rohkem osakesi, mida kiiremini nad
liiguvad. Et molekulide tihedus lisamine integraali on vajalik, kuna ühemõõtmelisel
juhul sõltub oskeste voog läbi "kontrollpinna" lisaks viimase
pindalale ka osakeste kiirusest: sama tiheduse korral jõuab
ajaühikus pinda läbida seda rohkem osakesi, mida kiiremini nad
liiguvad. Et molekulide tihedus 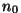 on praeguse probleemi
seisukohalt ebaoluline, tähistame seda sisaldava konstandi
lihtsalt on praeguse probleemi
seisukohalt ebaoluline, tähistame seda sisaldava konstandi
lihtsalt 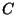 -ga ja leiame ta (pärast võrrandi mõlemate poolte -ga ja leiame ta (pärast võrrandi mõlemate poolte
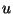 -ga läbi jagamist) normeerimistingimuse
abil. Kui nii talitada, saame osakeste suhtelise tõenäosuse
jaotuse, mis näitab, kui suure osa molekulide koguarvust
moodustavad antud kiirusega (kiiruste vahemikus) antud suunas liikuvad
osakesed. -ga läbi jagamist) normeerimistingimuse
abil. Kui nii talitada, saame osakeste suhtelise tõenäosuse
jaotuse, mis näitab, kui suure osa molekulide koguarvust
moodustavad antud kiirusega (kiiruste vahemikus) antud suunas liikuvad
osakesed.
|
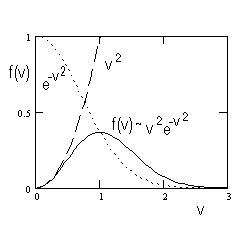 Maxwelli jaotus ja selle "piirajad" - funktsioonid v2 ning
Maxwelli jaotus ja selle "piirajad" - funktsioonid v2 ning 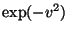
Integraalse jaotusfunktsiooni saame diferentsiaalse jaotusfunktsiooni integreerimisel.
NB! Maxwelli jaotuse tuletamine on lisatekst ning ei kuulu kohustusliku (eksamil kontrollitava) materjali hulka. Jaotust ennast ning sellele vastavat kõverat tuleb tunda ning osata seletada.
Kõik diferentsiaalsed jaotusfunktsioonid normeeritakse, st. jagatakse läbi vastava funktsiooni integraaliga üle kogu määramispiirkonna.
|
|
Integreerime nüüd saadud funktsiooni. Selleks teeme muutuja
vahetuse:
saades integraali
kust
|
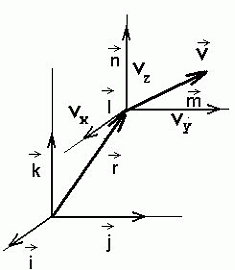 Faasiruum: iga osakest iseloomustab lisaks kohavektorile
Faasiruum: iga osakest iseloomustab lisaks kohavektorile 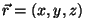 ka kiirusvektor
ka kiirusvektor 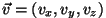 .
Kokku kuus koordinaati. .
Kokku kuus koordinaati.
|
See oleks siis tõenäosus, et osake liigub 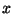 -telje suunas
kiirusega -telje suunas
kiirusega
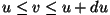 . Tõenäosuse, et osake liigub mingis
suvalises suunas kiirusega . Tõenäosuse, et osake liigub mingis
suvalises suunas kiirusega
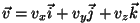 , saame,
kui korrutame omavahel kolm tõenäosust: , saame,
kui korrutame omavahel kolm tõenäosust:
- et
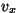 on vahemikus on vahemikus
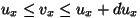 -- -- 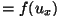 ; ;
- et
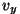 on vahemikus on vahemikus
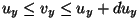 -- -- 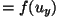 ; ;
- et
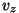 on vahemikus on vahemikus
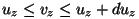 -- -- 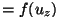 . .
Seega
Nüüd teeme kaks matemaatilist nippi:
esiteks viime eksponendid
ühisele astendajale, saades
teiseks asendame integreerimisel korrutise 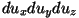 sfäärilise kihiga
faasiruumis sfäärilise kihiga
faasiruumis 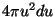 .
Tulemuseks saame:
Kuidas siit jõuda Maxwelli jaotuse traditsioonilise kujuni,
jäägu teie endi leida.
Mida me näeme? Nii jaotuse enda kui ka eksponentliikme astendaja
kordajad sõltuvad suurusest .
Tulemuseks saame:
Kuidas siit jõuda Maxwelli jaotuse traditsioonilise kujuni,
jäägu teie endi leida.
Mida me näeme? Nii jaotuse enda kui ka eksponentliikme astendaja
kordajad sõltuvad suurusest 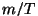 . Mida väiksem on see suurus
(mida kõrgem temperatuur või mida väiksem osakese mass), seda
kiiremini muutub jaotusfunktsioon. Kui tegur on suur
(temperatuur madal või osakeste mass suur), on kõver laugjam ja madalam.
Maxwelli jaotus, nagu teisedki shoti füüsiku J. C. Maxwelli
valemid on saadud puhtmatemaatilistest kaalutlustest,
tuginedes lisaks katseandmetele veel teatud puhtfilosoofilist
laadi eeldustele (molekulid on punktikujulised massiga osakesed,
elektri- ja magnetväli ei sõltu keskkonnast jne.). See on uut
tüüpi lähenemine füüsikalisele maailmatunnetusele -
lähtumine formaal-loogilisest vaatepunktist. Oluline on,
et erinevalt Newtoni, Ampere'i, Ohm'i jt. empiirilistest seadustest tuletatakse
siin matemaatiliselt ka valemite konstandid. See on
meetod, mida tänapäeval tuntakse teoreetilise füüsika nime
all. . Mida väiksem on see suurus
(mida kõrgem temperatuur või mida väiksem osakese mass), seda
kiiremini muutub jaotusfunktsioon. Kui tegur on suur
(temperatuur madal või osakeste mass suur), on kõver laugjam ja madalam.
Maxwelli jaotus, nagu teisedki shoti füüsiku J. C. Maxwelli
valemid on saadud puhtmatemaatilistest kaalutlustest,
tuginedes lisaks katseandmetele veel teatud puhtfilosoofilist
laadi eeldustele (molekulid on punktikujulised massiga osakesed,
elektri- ja magnetväli ei sõltu keskkonnast jne.). See on uut
tüüpi lähenemine füüsikalisele maailmatunnetusele -
lähtumine formaal-loogilisest vaatepunktist. Oluline on,
et erinevalt Newtoni, Ampere'i, Ohm'i jt. empiirilistest seadustest tuletatakse
siin matemaatiliselt ka valemite konstandid. See on
meetod, mida tänapäeval tuntakse teoreetilise füüsika nime
all.
|
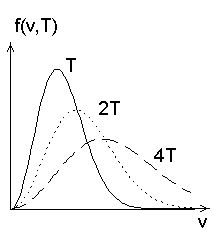 Maxwelli jaotus erinevatel temperatuuridel.
Maxwelli jaotus erinevatel temperatuuridel.
Maxwelli jaotus pole leitud katsest, vaid tuletatud matemaatiliselt.
|
|
Järeldused Maxwelli valemist. Lisaks juba tuntud
molekulide ruutkeskmisele kiirusele
saame leida veel keskmise kiiruse
ning, lähtudes funktsiooni ekstreemumi tingimusest
molekulide tõenäoseima kiiruse
|
Maxwelli jaotuse integreerimise teel on võimalik leida nii molekulide keskmist, ruutkeskmist kui tõenäoseimat kiirust.
|
Kulgliikumise jaoks tuletatud jaotust kiiruste järgi saab
üldistada suvalise kineetilise energia kohta käivaks, kui
asendada Maxwelli jaotuses
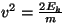 . .
Siis
ning
Saadud valem on oluline erisoojuste klassikalises teoorias ning
faasiüleminekute uurimisel.
Maxwelli jaotuse eksperimentaalsest
kontrollist. Kiiruste jaotust on suhteliselt lihtne uurida:
tuleb tekitada osakeste voog ning juhtida sellest eraldatud lõik
liikuvale ekraanile. Praktikas on piisava täpsusega katse
teostamine omajagu keeruline ning see õnnestus alles 1920. a.
Osakeste allikat (hõbetatud plaatinaniit) ümbritsevad kaks sama
nurkkiirusega pöörlevat koaksiaalset (samateljelist. ld. co+axis,
telg) silindrit, milledest
sisemise seina on lõigatud teljega paralleelne pilu. Sellest
väljuv molekul jõuab välimise silindrini aja
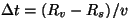 pärast, mistõttu tema langemiskoht ei asu mitte
sisemise pilu vastas, vaid on nihkunud pärast, mistõttu tema langemiskoht ei asu mitte
sisemise pilu vastas, vaid on nihkunud
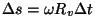 võrra. Välimisele silindrile sadestunud hõbedakihi
paksus on seetõttu võrdeline vastava kiirusega osakeste
esinemissagedusega, ehk, teiste sõnadega - osakeste
diferentsiaalse jaotusfunktsiooni võrra. Välimisele silindrile sadestunud hõbedakihi
paksus on seetõttu võrdeline vastava kiirusega osakeste
esinemissagedusega, ehk, teiste sõnadega - osakeste
diferentsiaalse jaotusfunktsiooni 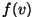 väärtusega antud
kiiruse juures.
Kirjeldatud katset on korratud erinevate ainete ning ka eri
tüüpi katseseadmete abil. Tulemused on piisavalt heas kooskõlas
Maxwelli valemiga.
Sellegipoolest loetakse Maxwelli valemi
peamiseks väärtuseks tema heuristilist väärtust (kr. heurisko - leian). Teadmine, et mingi süsteemi komponentide
energiad jaotuvad kindla seaduspärasuse järgi, võimaldab
modelleerida ("panna valemeisse") paljusid juhuslikkusel
põhinevaid nähtusi. Üht neist kirjeldame kevadsemestri viimase
loengu juurde antud lisatekstis. väärtusega antud
kiiruse juures.
Kirjeldatud katset on korratud erinevate ainete ning ka eri
tüüpi katseseadmete abil. Tulemused on piisavalt heas kooskõlas
Maxwelli valemiga.
Sellegipoolest loetakse Maxwelli valemi
peamiseks väärtuseks tema heuristilist väärtust (kr. heurisko - leian). Teadmine, et mingi süsteemi komponentide
energiad jaotuvad kindla seaduspärasuse järgi, võimaldab
modelleerida ("panna valemeisse") paljusid juhuslikkusel
põhinevaid nähtusi. Üht neist kirjeldame kevadsemestri viimase
loengu juurde antud lisatekstis.
|
 Maxwelli jaotuse kontroll.
Maxwelli jaotuse kontroll.
Kiired molekulid (kõvera ots B) jõuavad välimise silindrini varem kui aeglased (ots A). Tekkiva metallikihi paksus vastab Maxwelli jaotusele.
|
|
Ülekandenähtused. Maxwelli jaotuse abil saame
arvutada ka gaasi mittetasakaalulisi olekuid, kus mõni
olekuparameeter (näiteks temperatuur või keemiline koostis) on
vaadeldava ruumi eri osades erinev. Selline mittetasakaalulisus toob
kaasa energia, massi või liikumishulga ülekandumise ühest ruumiosast
teise, siit ka nähtuse nimetus.
Tehnilistes ülesannetes puutume kõige sagedamini kokku just loetletud
kolme suuruse ülekandumisega. Insenerifüüsikas räägitakse vastavalt
soojusjuhtivusest (energia ülekanne), difusioonist (massi
ülekanne) ja sisehõõrdest (impulsi ehk liikumishulga ülekanne).
Kõigil kolmel juhul iseloomustab lähteolekut mingi parameetri
(temperatuuri 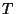 , kontsentratsiooni , kontsentratsiooni 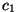 , voolukiiruse , voolukiiruse 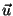 )
ebaühtlane jaotus, mida saab kirjeldada väljafunktsiooniga
(parameetri väärtus sõltuvalt asukohast). Ülekande kiirus on alati
võrdeline vaadeldava suuruse gradiendiga (vt. loeng 5),
võrdetegurit aga saab leida keskmise kiiruse kaudu. )
ebaühtlane jaotus, mida saab kirjeldada väljafunktsiooniga
(parameetri väärtus sõltuvalt asukohast). Ülekande kiirus on alati
võrdeline vaadeldava suuruse gradiendiga (vt. loeng 5),
võrdetegurit aga saab leida keskmise kiiruse kaudu.
|
Ülekandenähtuste all mõistame soojuse, keemilise koostise, impulsi või muu parameetri levikut gaasis.
|
Näitena vaatame lihtsamat juhtu, kus parameetri muutus toimub kindlas
suunas, näiteks 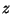 -telje sihis. Gradient asendub sel juhul lihtsa
tuletisega ning valemiteks saame:
Viimane valem väljendab meile juba hüdrodünaamikast tuntud
hõõrdejõudu, teised aga ajaühikus pinda -telje sihis. Gradient asendub sel juhul lihtsa
tuletisega ning valemiteks saame:
Viimane valem väljendab meile juba hüdrodünaamikast tuntud
hõõrdejõudu, teised aga ajaühikus pinda 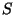 läbinud gaasi massi läbinud gaasi massi
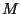 või soojushulka või soojushulka 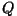 . Kõik konstandid on avaldatavad keskmise
kiiruse . Kõik konstandid on avaldatavad keskmise
kiiruse 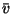 ning molekuli vaba tee pikkuse ning molekuli vaba tee pikkuse
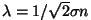 kaudu:
Keskmine kiirus on leitav Maxwelli jaotusest; vaba tee pikkus
sõltub aga gaasi tihedusest kaudu:
Keskmine kiirus on leitav Maxwelli jaotusest; vaba tee pikkus
sõltub aga gaasi tihedusest 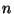 ning ühest senini empiirilisest
suurusest, nn molekuli efektiivsest ristlõikepindalast
(väljendab molekulaarjõudude mõjuraadiust) ning ühest senini empiirilisest
suurusest, nn molekuli efektiivsest ristlõikepindalast
(väljendab molekulaarjõudude mõjuraadiust) 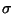 : :
|
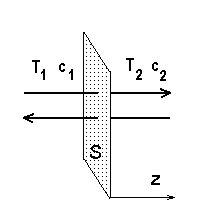 Soojusülekanne ja difusioon.
Soojusülekanne ja difusioon.
Temperatuuride (kontsentratsioonide) erinevus T1 - T2 (või konsentratsioonide erinevus c1 - c2) toob kaasa energia (või massi) voo läbi pinna S.
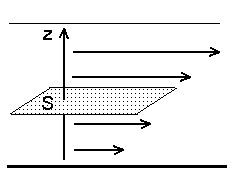 Sisehõõrdumine.
Sisehõõrdumine.
Aeglasemad molekulid liiguvad läbi pinna S, aeglustades gaasi voolamist ülemistes kihtides.
|