7. Vedelike voolamine.
Vedelike (gaaside) mehaanika. Siiani rõhutasime kõikjal kehade jäikust - jõudude mõjul need
hakkasid kas liikuma või pöörlema, aga tegid seda tervikuna.
Kogemusest teame aga, et looduses on hulgaliselt kehi, mis pole
tervikuna nihutatavad (kui nad just tahkest ainest anumasse pole
suletud). Nende kehade - vedelike ja gaaside - liikumist saab
samuti arvutada.
Vedelikke ja gaase eristab tahketest kehadest see, et neil puudub
kindel kuju. Iga vedeliku või gaasi osake liigub iseseisvalt,
teda võib vaadelda kui masspunkti (või ruumielementi). Kui
räägitakse vedeliku liikumisest (näiteks voolamisel), mõeldakse
selle all vedelikuosakeste liikumist.
Kui suur peaks see osake olema? Newtoni mehaanika, mis kasutab
pidevaid funktsioone, nõuab, et võrrandid kehtiksid "kuitahes
väikeste osakeste korral". Klassikalise füüsika seisukohalt peab
vedelik olema pidev keskkond - ainult siis saame rakendada
diferentsiaalarvutust. Nii valime oma joonistel "ruumielemendi"
piisavalt suure (et joonis loetav oleks) ja vajaduse korral vähendame
seda kuni "lõpmata väikese suuruseni".
|
Mehaanikas eristatakse aine kolme olekut järgnevalt:
- Tahke keha
säilitab liikumisel oma kuju ja ruumala;
- Vedelik
säilitab liikumisel oma (kogu)ruumala, kuid ei säilita kuju;
- Gaas
ei säilita ei kuju ega ruumala, vaid täidab kogu olemasoleva ruumi.
|
NB! Need lõpmata väikesed osakesed ei ole molekulid!
Molekulid, millel on kindel mass ja mõõtmed ja mis liiguvad
kaootiliselt ning väga suurte kiirustega, tulevad mängu gaaside
kirjeldamisel. Klassikalise hüdrodünaamika vedelik on pidev, tema
osake võib (põhimõtteliselt!) olla kuitahes väike.
|
Mehaanika käsitleb vedelikku pideva keskkonnana.
|
|
Et leida vedeliku liikumise võrrandit, peame oskama
matemaatiliselt kirja panna vedelikuosakestele mõjuvaid jõude.
Kuna osakesi mõjutavad kõige sagedamini teised (naaber-)osakesed,
on vaja suurust, mis iseloomustaks neid jõudusid. Et me oskame
mõõta-arvutada tahketele kehadele mõjuvaid jõude, kasutamegi
vedelike uurimisel nende kontakti tahkete kehadega.
Kõige
tavalisemaks uurimisvahendiks on silindriline anum, milles
liigub tihedalt kolb. Kui sellele kolvile mõjuda jõuga, kandub
see jõud üle kolvi all anumas olevale vedelikule ning meil on täielik alus
oletada, et jõud vedeliku sees on samaväärsed vedeliku ja kolvi
vaheliste jõududega.
Katse näitab, et oluline pole mitte kolvile mõjuv jõud, vaid
selle jagatis kolvi pindalaga. Kui meil on kaks ühendatud
silindrit, mille läbimõõdud on erinevad, peab tasakaalu
saavutamiseks suurema läbimõõduga silindris liikuvale kolvile
mõjuma suurema jõuga.
|
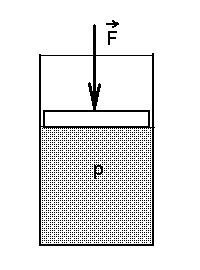
Vedelik kolvi all
|
|
Täpne mõõtmine näitab, et see jõud on
pöördvõrdeline kolvi pindalaga, ei sõltu silindri kujust ega
asendist.
Et tegu on vedeliku omadusega, taipas esimesena prantsuse
looduseuurija, rohkem filosoofina tuntud Blaise Pascal,
tema nime järgi on nimetatud nii vastav seadus kui ka rõhu ühik.
Rõhk on vaadeldavale kehale mõjuv rõhumisjõud
pinnaühiku kohta
Pascal'i seadus:
Vedelikud ja gaasid annavad rõhku
edasi kõigis suundades ühteviisi.
|
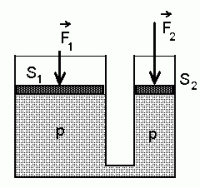
Ühendatud silindrid
|
Kaks lihtsat ja lühikest lauset, kerge pähe õppida kuid raske
mõista. Esiteks, kui rõhk ei sõltu suunast, siis peab ta olema
skaalar. Et jõud on vektor, peab definitsioonist tulenevas
valemis
|
Rõhu ühikuks SI süsteemis on paskal, (P) mis vastab rõhumisjõule üks njuuton ruutmeetri kohta.
|
olema lisaks jõule veel üks vektoriaalne suurus. See võib olla
vaid pindala - sel juhul oleks võimalik kirjutada näiteks
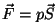 . .
Niisiis peab füüsikas pindala olema suunatud suurus - vektor. Aga
seda ta ju ongi - igal pinnatükil on kindel ruumiline
orientatsioon, mida väljendab temale tõmmatud ristsirge e.
normaal.
Pindala vektoriks loemegi vektorit, mille moodul
võrdub pinnatüki pindalaga, suund aga ühtib selle pinna
normaaliga.
Millisesse suunda kahest võimalikust on vektor
suunatud, on meie endi otsustada. See suund on kokkuleppeline, nagu
pöörleva liikumise aksiaalvektoreilgi. Kui jutt on anumasse suletud
gaasi rõhust,
võetakse pinna vektori suund väljapoole. Et rõhumisjõu suund
on samuti anumast väljapoole, peab rõhk olema alati
positiivne suurus (rõhkude vahe muidugi mitte!).
|
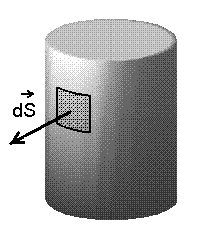
Pinnatükk dS vektorina
|
Kui rääkida rõhust vedeliku sees, tuleb meil kujutleda mingit
vedelikuosakest ja sellele mõjuvaid jõude. Tasakaalu korral
vedelik seisab paigal, vedelikuosakesed on järelikult liikumatud
ja neile mõjuvate jõudude resultant null. See on võimalik vaid
siis, kui rõhk on sõltumatu suunast - veel üks tõestus Pascali
seadusele.
Rõhk raskusjõu väljas. Vedeliku omapäraks
gaasidega võrreldes on pinna olemasolu. Meile harjumuspärane
horisontaalne tasane pind kujuneb raskusjõu mõjul - vedeliku
osakesed võtavad sellise asendi, kus neile mõjuvad jõud on
tasakaalus.
Kui veepind ei oleks horisontaalne, tekiks pinnal
asuvatel osakestel "kaldpinna efekt" - raskusjõu pinnaga
paralleelse komponendi mõjul hakkaks osakesed alla libisema; see
liikumine kestaks seni, kuni pind võtab horisontaalse asendi
nii, et raskusjõud on pinnaga risti.
|
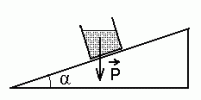
Vedelik kaldpinnal
|
|
Raskusjõud mõjub ka vedeliku sees.
Seetõttu lisandub iga vedelikuosakese jaoks lisaks
naaberosakeste rõhule ka osakese enda kaal. Koos sellega
muutub tasakaaluvõrrand.
Näiteks kuubikujulise ruumiosa jaoks (vt.
joon.) kirjutame tasakaaluvõrrandi
Et külgtahkudele mõjuvad jõud on
võrdsed-vastassuunalised, saame
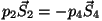 ning ning
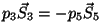 . Võrrandisse jääb kolm
liiget: . Võrrandisse jääb kolm
liiget:
|
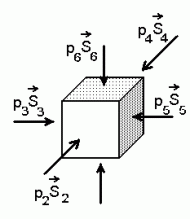
Rõhutasakaal:
Et kuup paigal seisaks, peavad tema tahkudele mõjuvad jõud olema võrdsed
|
kus 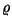 on vedeliku tihedus ja on vedeliku tihedus ja 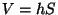 kuubi ruumala. Et
kõik need vektorid on samasihilised, võime kirjutada
skalaarse võrrandi, võttes märgid vastavalt vektorite suunale:
Siin kuubi ruumala. Et
kõik need vektorid on samasihilised, võime kirjutada
skalaarse võrrandi, võttes märgid vastavalt vektorite suunale:
Siin 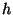 on kuubi kõrgus. on kuubi kõrgus.
Kui kuubi ülaserv asub vedeliku
pinnal, on 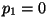 ning valem saab lihtsa kuju: ning valem saab lihtsa kuju:
kus 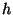 tähistab sügavust - kaugust vedeliku
pinnani. tähistab sügavust - kaugust vedeliku
pinnani.
Näiteks saame vee rõhuks 100 m sügavusel
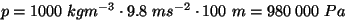 . .
NB! Pöörame tähelepanu ühele olulisele momendile vedelike
mehaanikas:
vedelikuhulga mass avaldatakse tiheduse kaudu.
Kui tahketel kehadel oli alati kindel kuju ja seega ka kindel mass,
siis sõnaühend "vedeliku mass" ei oma mingit mõtet - me võime rääkida
vaid kindla vedelikuhulga massist.
Aga vedeliku hulka on iidsetest
aegadest saadik mõõdetud ruumalaühikute (kortel, toop, liiter) abil.
|
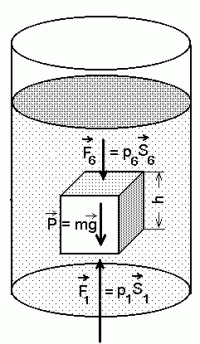
Tasakaal raskusjõuga:
Kuubi kaalu P peab tasakaalustama üleslükkejõud.
|
|
Kui meil on vaja teada mitte ruumala, vaid massi, peame liitrites
mõõdetud vedelikuhulga korrutama ühe liitri vedeliku massiga - seega
vedeliku tihedusega.
See lihtne tehe sisaldab aga varjatud eeldust, et vedeliku
tihedus on kõikjal ja alati ühesugune.
|
Kõigis veekogudes - ka veevärgi torudes - kasvab rõhk sügavuse h kasvades 9800 paskalit iga meetri kohta
|
Tegelikkuses on vedelikud
nagu tahked kehadki kokkusurutavad (tihedus sõltub rõhust), ka esineb
vedelikel soojuspaisumine (tihedus sõltub temperatuurist).
Õnneks on need muutused väga väikesed ja seepärast võib
klassikaline hüdrodünaamika neid mitte arvestada.
Et asi täpne oleks,
räägitakse sel juhul ideaalsest vedelikust, mille tihedus on
alati ühesugune, mis ei lähe kunagi keema ja mis voolab ilma
takistusteta.
|
Ideaalne vedelik ei muuda oma tihedust ja voolab takistuseta.
|
|
Rõhutasakaalu valemist raskusjõu väljas järeldub üks
hüdrostaatika tuntuimaid valemeid - Archimedese seadus.
Kujutame ette, et veekuubi asemel on meil samade mõõtmetega keha
tihedusega 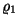 ja järelikult massiga ja järelikult massiga
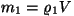 . Nüüd
pole see kuup enam tasakaalus: talle mõjub rõhkude vahest
tingitud üleslükkejõud . Nüüd
pole see kuup enam tasakaalus: talle mõjub rõhkude vahest
tingitud üleslükkejõud
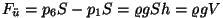 ning
keha kaal ning
keha kaal 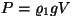 . Keha kaaluks vees saame . Keha kaaluks vees saame
 . .
Archimedese sõnastuses:
Vedelikku asetatud kehad
kaotavad oma kaalust osa, mis on võrdne keha poolt välja
tõrjutud vedeliku kaaluga.
Tõepoolest: kui 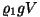 oli keha kaal, siis oli keha kaal, siis
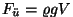 on
keha ruumalale vastava vedelikuhulga kaal, mida võib ju nimetada
ka välja tõrjutud vedeliku kaaluks. on
keha ruumalale vastava vedelikuhulga kaal, mida võib ju nimetada
ka välja tõrjutud vedeliku kaaluks.
Küsimus: Millistel tingimustel kehad ujuvad? Kui suur osa
nendest asub vee all?
|
Tahked kehad on vedelikus seda kergemad, mida suurem on nende ruumala
|
Voolav vedelik.
Kui rõhutasakaal mingil põhjusel puudub, hakkavad
vedelikuosakesed liikuma. Osakesele mõjuv jõud tähendab, et
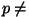 const. Sel juhul räägime rõhuväljast, mis on
skalaarne väli; sellisesse väljas sattunud osakestele mõjub
jõud ja nad hakkavad liikuma. Vedeliku liikumist nim.
voolamiseks ja seda uurib hüdrodünaamika. const. Sel juhul räägime rõhuväljast, mis on
skalaarne väli; sellisesse väljas sattunud osakestele mõjub
jõud ja nad hakkavad liikuma. Vedeliku liikumist nim.
voolamiseks ja seda uurib hüdrodünaamika.
Kui hüdrostaatika valemite tuletamisel lähtusime eeldusest, et
tihedus on konstantne (ei sõltu rõhust), siis nüüd peame tegema
veel ühe lihtsustava eelduse. Selleks on takistuseta voolavus e.
sisehõõrdejõudude puudumine. Mis jõud need on ja millest
sõltuvad, sellest edaspidi.
Takistuseta voolavat
mittekokkusurutavat vedelikku nim. ideaalseks vedelikuks
ning tema abil tuletatakse hüdrodünaamika põhivalemid. Üleminek
reaalsetele vedelikele tehakse hiljem vastavate parandusliikmete
sisseviimisega.
|
|
Kujutame lihtsuse mõttes torus voolavat vedelikku.
Voolamiskiirust saame määrata kahel viisil:
- märgistades
mõne vedelikuosakese ning mõõtes selle kiirust nagu tahkete
kehade korral;
- mõõtes torust välja voolava vedeliku
hulka.
Reaalse vedeliku korral on osakeste kiirused torus erinevad
ning seetõttu kõlbab voolukiiruseks vaid teine variant. Ideaalse
vedeliku korral on kiirused võrdsed ning kirjeldused
ekvivalentsed. Nii saame toru aja 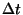 jooksul mistahes ristlõiget läbivaks
veehulgaks jooksul mistahes ristlõiget läbivaks
veehulgaks
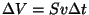 ; kiiruseks ajaühikus toru
ristlõiget läbinud vedeliku hulga järgi on seega suhe ; kiiruseks ajaühikus toru
ristlõiget läbinud vedeliku hulga järgi on seega suhe
Hüdrodünaamika põhivõrranditeks on pidevuse teoreem ja
Bernoulli võrrand. Mõlemad kujutavad endast mehaanika
jäävusseaduste formuleeringuid hüdrodünaamika jaoks. Lihtsuse
mõttes alustame ühemõõtmelisest voolamisest - voolamisest torus.
Pidevuse teoreem:
Vedeliku voolamisel muutuva ristlõikega torus on
voolamise kiirus pöördvõrdeline toru ristlõike pindalaga.
|
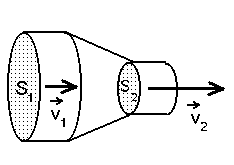
Pidevuse teoreem: mida peenem toru, seda suurem voolamiskiirus.
|
|
Tõestada pole siin midagi: kuna vedelik torust välja ei pääse
ning ka kokku ei anna teda suruda, peab suvalist ristlõiget sama
ajavahemiku vältel läbima võrdne vedelikuhulk. Võrdsustades
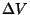 väärtused eri ristlõigetes, saame otsitava valemi. väärtused eri ristlõigetes, saame otsitava valemi.
Seega kujutab pidevuse teoreem endast tegelikult aine jäävuse
seadust.
|
|
Bernoulli võrrand:
See on energia jäävuse seadus. Vaatame joonisel
kujutatud kaldu asetsevat muutuva ristlõikega toru. Valime kaks
ristlõiget: ühe kõrgusel 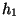 ja pindalaga ja pindalaga 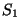 , teise
kõrgusel , teise
kõrgusel 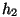 ristlõikega ristlõikega 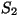 ning arvutame vedeliku
voolamisel läbi sellise toru ajavahemikul ning arvutame vedeliku
voolamisel läbi sellise toru ajavahemikul 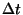 tehtava
töö: tehtava
töö:
(esimene
liige on võetud negatiivne, kuna siin on ristlõikepinna vektori
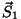 suund vastupidine kiirusvektori suund vastupidine kiirusvektori 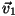 suunaga).
Energia jäävuse seaduse kohaselt peab see olema võrdne
mehaanilise koguenergia muuduga
Asendades massi tiheduse ja ruumala kaudu suunaga).
Energia jäävuse seaduse kohaselt peab see olema võrdne
mehaanilise koguenergia muuduga
Asendades massi tiheduse ja ruumala kaudu
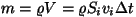 , rakendades pidevuse teoreemi , rakendades pidevuse teoreemi 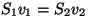 ning koondades sarnased liikmed, saamegi ülaltoodud võrduse.
ning koondades sarnased liikmed, saamegi ülaltoodud võrduse.
|
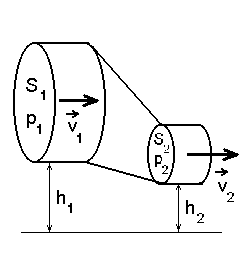
Bernoulli võrrand: rõhk p sõltub nii voolamiskiirusest kui toruosa kõrgusest .
|
Järeldused Bernoulli võrrandist:
Horisontaalses torus on voolava vedeliku rõhk seda väiksem,
mida suurem on voolamise kiirus.
Tõepoolest, kui 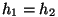 , saame , saame
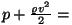 const.
Seega peab kiiruse suurenemisel esimene liidetav vähenema. const.
Seega peab kiiruse suurenemisel esimene liidetav vähenema.
Reservuaarist välja voolava vee kiirus on niisama suur, kui
on lõppkiirus veetaseme ja väljavooluava
kõrguste vahele vastavalt kõrguselt kukkumisel.
Lähtume sellest, et rõhk nii reservuaari pinnal kui ava kõrgusel
on sama. Järelejäänud valemist
kaob veel liige kus 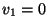 .
Kui .
Kui 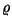 -ga läbi jagada, jääb -ga läbi jagada, jääb
sama
kiirus, mille saavutaks vabalt langev keha kõrguste vahe
 korral. korral.
Ka rõhu valem raskusjõu väljas on tuletatav Bernoulli võrrandist
juhul, kus vedelik seisab (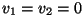 ). ).
|
|
Lisatekst: Pideva keskkonna hüdrodünaamika
Tuletatud valemeid on võimalik kirja panna ka "torude" abita.
Selleks vaatame vedelikku ruumi täitva pideva keskkonnana, kus
iga ruumipunkti jaoks saab määrata rõhu, vedeliku tiheduse ja
voolamiskiiruse. Kaks esimest on teadupärast skalaarsed
suurused, kolmas aga vektor. Nii et matemaatika seisukohalt on
meil tegemist kahe skalaarse ja ühe vektorväljaga, mille
uurimiseks kasutame matemaatikast tuntud vektoranalüüsi
meetodeid.
|
Pideva keskkonna kirjeldamisel kasutab hüdrodünaamika vektoranalüüsi meetodeid.
|
Pidevuse teoreemi analoogi leidmiseks eraldame ruumis kinnise
pinnaga 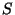 piiratud ruumiosa piiratud ruumiosa 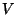 . Läbi pinnaelemendi ajaühikus
välja voolava vedeliku hulgaks saame
ning kogu
ruumiosast . Läbi pinnaelemendi ajaühikus
välja voolava vedeliku hulgaks saame
ning kogu
ruumiosast 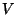 väljuva voo integraalina väljuva voo integraalina
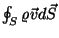 .
Et vaadeldavas ruumiosas olev vedelikuhulk
selle tõttu väheneb, saame aine jäävuse seaduse kujul
Kui nüüd lasta "vedelikuosakesel" muutuda lõpmata väikeseks, st. tema
ruumala
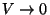 , jääb vasaku poole integraalist alles vaid
integreeritav avaldis , jääb vasaku poole integraalist alles vaid
integreeritav avaldis 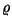 ; kokku näitab vasak pool tiheduse muutumise kiirust ; kokku näitab vasak pool tiheduse muutumise kiirust
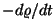 . Ka parem pool läheneb nullile, aga kuidas, seda me ei
tea. Kui teisendada võrrandi paremat poolt Gaussi-Ostrogradski
teoreemi abil:
saame viia mõlemad liikmed ühele poole võrdusmärki:
Et integraal on üle suvalise ruumala, järeldub siit integrandi
võrdsus nulliga. Üldjuhul, kus muutuda võib ka tihedus, võime
teise liikme lahti kirjutada korrutise diferentseerimise reegli
kohaselt:
mis ongi hüdrodünaamika pidevuse võrrand. . Ka parem pool läheneb nullile, aga kuidas, seda me ei
tea. Kui teisendada võrrandi paremat poolt Gaussi-Ostrogradski
teoreemi abil:
saame viia mõlemad liikmed ühele poole võrdusmärki:
Et integraal on üle suvalise ruumala, järeldub siit integrandi
võrdsus nulliga. Üldjuhul, kus muutuda võib ka tihedus, võime
teise liikme lahti kirjutada korrutise diferentseerimise reegli
kohaselt:
mis ongi hüdrodünaamika pidevuse võrrand.
Vedeliku voolamise kirjeldamiseks paneme kirja Newtoni II
seaduse pideva keskkonna tarbeks:
Jällegi on meil ühel pool võrdusmärki pind-, teisel pool
tavaline kolmekordne (ruum)integraal. Gauss-Ostrogradski
teoreem kehtib ka siin kujul
Korrates pidevuse võrrandi tuletamisel kasutatud võtteid, saame
mis olekski vedeliku liikumisvõrrand rõhuväljas juhul, kui
voolukiirus on ekvivalentne osakese liikumiskiirusega.
|
|
Reaalsed vedelikud.
Tundes ideaalse vedeliku voolamise seadusi, on meil suhteliselt
lihtne kirjeldada ka reaalsete vedelike liikumist. Selleks lisame
juba olemas olevatesse võrranditesse kaks vedelikku iseloomustavat
näitajat:
-
Pindpinevus on vedeliku pinnakihi omadus, mis väljendub
vastuseisus vedeliku pinda suurendavatele jõududele.
Pindpinevust saab väljendada numbrilise kordaja - nn.
pindpinevusteguri kaudu. See kordaja näitab, kui palju tuleb teha
tööd vedeliku pinna suurendamiseks 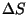 võrra: võrra:
|
Pindpinevus tekib vedeliku sisejõudude toimel ning püüab vähendada vedelikuosakese välispinda.
|
loomulikult on erinevatel vedelikel erinev pindpinevustegur 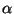 .
Ka sõltub teguri väärtus välistingimustest nagu temperatuur, rõhk,
vedelikku ümbritseva gaasi koostis. .
Ka sõltub teguri väärtus välistingimustest nagu temperatuur, rõhk,
vedelikku ümbritseva gaasi koostis.
-
Sisehõõre väljendab vedeliku voolamisel tekkivat
takistusjõudu. Selle jõu tulemusel voolavad paigalseisva pinna
(näiteks jõepõhja) lähedal olevad veekihid aeglasemalt kui sellest
kaugemal olevad kihid.
Ka seda jõudu saab kirjeldada antud vedelikku
iseloomustava suuruse - sisehõõrdeteguri abil.
|
Sisehõõrdumine tekib samuti sisejõudude toimel ning takistab vedeliku voolamist (vähendab kiirust).
|
|
Nii pindpinevuse kui sisehõõrde tekkepõhjuseks on molekulide
vahelised jõud. Nende tänapäevane kirjeldus kuulub
kvant-teooriasse; meie oma üldfüüsika kursusega nii kaugele ei jõua.
Igapäeva-vajadusi rahuldab nende jõudude katseline kirjeldus (nn.
empiirilised valemid), mille koostamist ja rakendamist õpite
vastavate laboritööde teoreetilises osas.
|
|