Loeng 6. Tahke keha pöörlemine.
Pöördliikumisest on seni juttu olnud kahel korral: staatika osas, kus
meie esimest masinat pööras jõumoment ning kinemaatika osas,
kus tõime näite kõva keha pöörlemisest kui ühedimensionaalsest
liikumisest.
Newtoni dünaamika ei erista pöördliikumist kulgevast liikumisest.
Kuna sealsed valemid käivad punktmassi kohta, polegi neid
võimalik eristada - punkt, millel pole joonmõõtmeid, ei saagi
pöörelda.
|
Pöörlemise all mõistetakse jäiga, liikumise käigus mitte deformeeruva keha asendi (orientatsiooni) muutust.
Pöörleva keha erinevad osad liiguvad piki erinevaid trajektoore, kuid säilitavad oma vastastikuse asendi.
|
Mispärast? Vihje: pange punktist telg läbi ja proovige
defineerida pöördenurka!
Lõplike mõõtmetega keha pöörlemise dünaamika.
Kui me tegime kulgliikumise valemeid, märkisime, et keha liikumise
kirjeldamiseks piisab ühe punkti liikumisest, kuna kõik teised
liiguvad samamoodi.
Pöörlemist eristab kulgliikumisest just see, et
samasuguse liikumise tingimus pole enam täidetud. Iga pöörleva
keha punkt liigub kulgevalt, kuid nende trajektoorid ruumis on
erinevad.
Kuna keha jääb pööreldes siiski tervikuks, on need
trajektoorid aga omavahel seotud - seetõttu saab võimalikuks
kirjeldada keha pöörlemist ühe võrrandiga. Muidugi üksnes
juhul, kui keha kuju ei muutu. Aga see eeldus oli vajalik ka
kulgliikumise korral.
Pöörlemise põhivõrrandite kirjapanek olekski esimene näide Newtoni
seaduste kollektiivsest rakendamisest. Pöörlev keha jagatakse
lõpmata väikesteks osadeks, mille liikumist saab kirjeldada
kulgliikumise valemite abil. Neile valemitele lisanduvad
keha koos püsimise matemaatilised tingimused.
Eraldame vaadeldavast kehast tükikese, mille mass on 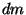 . Olgu selle
tükikese kaugus pöörlemisteljest . Olgu selle
tükikese kaugus pöörlemisteljest 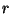 ja mõjugu temale jõud ja mõjugu temale jõud 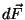 .
Tükike peaks selle jõu mõjul hakkama liikuma jõu suunas kiirendusega .
Tükike peaks selle jõu mõjul hakkama liikuma jõu suunas kiirendusega
Peaks, aga ei saa. Pöörlemine tähendab, et keha need punktid, mis
asuvad pöörlemisteljel, jäävad paigale. Kui meie poolt vaadeldav
tükike liiguks telje suhtes, peaks keha kuju muutuma - see aga pole
lubatud. Keha kuju säilib vaid juhul, kui tükike (koos kogu kehaga!) pöördub ümber telje, st. liigub risti nii telje kui ka teda teljega ühendava sirglõiguga.
Seetõttu ei mõjuta pöörlemist mitte kogu jõud 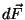 ,
vaid tema see komponent, mis on nii telje kui ,
vaid tema see komponent, mis on nii telje kui 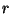 -ga risti. -ga risti.
|
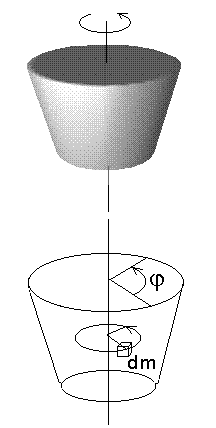
Pöörlev keha: iga tükike dm liigub piki ringjoonelist trajektoori
|
|
Katsume nüüd kirja panna dünaamika põhivõrrandi - Newtoni II seaduse
- selle tükikese kohta. Et kõik need diferentsiaalid meid segadusse
ei ajaks, kujutame, et tegu on "normaalse" punktmassiga 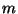 ja
"normaalse" jõuga ja
"normaalse" jõuga 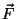 . Veel oletame, et jõud mõjub risti pöörlemisteljega. Selle jõu mõjul saab tükike kiirenduse . Veel oletame, et jõud mõjub risti pöörlemisteljega. Selle jõu mõjul saab tükike kiirenduse
| |
kus
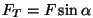 ja ja 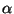 on nurk jõuvektori on nurk jõuvektori 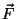 ning
tükikest pöörlemisteljega ühendava raadiuse ning
tükikest pöörlemisteljega ühendava raadiuse 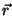 suuna vahel.
Nagu jooniselt näeme, on aga suuna vahel.
Nagu jooniselt näeme, on aga
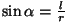 , kus l on
jõu , kus l on
jõu 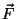 õlg. Saame: õlg. Saame:
kus 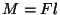 on jõu on jõu 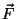 moment ette antud telje suhtes. moment ette antud telje suhtes.
Katsume siit jõuda pöörlemise kinemaatika valemis olevate suurusteni.
Pöörde ulatust mõõtis seal pöördenurk 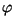 , mille esimeseks
tuletiseks aja järgi oli nurkkiirus , mille esimeseks
tuletiseks aja järgi oli nurkkiirus
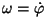 ning teiseks
tuletiseks nurkkiirendus ning teiseks
tuletiseks nurkkiirendus
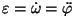 . Et pöördenurka
mõõdeti radiaanides (ringjoone kaare pikkuse ja raadiuse suhe!), on
pöördenurga suuruseks . Et pöördenurka
mõõdeti radiaanides (ringjoone kaare pikkuse ja raadiuse suhe!), on
pöördenurga suuruseks
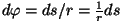 ning vastavalt ning vastavalt
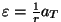 . .
Pöörlemise dünaamika põhivõrrand tuleb nüüd lihtsalt:
|
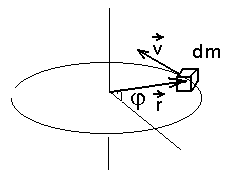
Tükikese 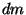 liikumist saab kirjeldada tema kohavektori liikumist saab kirjeldada tema kohavektori 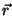 ning pöördenurga ning pöördenurga 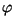 abil. Igal tükikesel on oma kindel kohavektor; pöördenurk aga on kõigile ühine. abil. Igal tükikesel on oma kindel kohavektor; pöördenurk aga on kõigile ühine.
|
kus 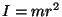 on meie "tükikese" inertsimoment. on meie "tükikese" inertsimoment.
Katsume leitut üldistada lõpliku kuju ja mõõtmetega keha kohta.
Selleks tuleb leida keha kui terviku inertsimoment ja kehale mõjuv
jõumoment. Inertsimomendi saame, kui liidame kokku kõigi tükikeste
inertsimomendid:
Seda saab teisendada integraaliks, kui keha on ühtlase tihedusega,
st. valmistatud mingist kindla tihedusega materjalist (puust, rauast
jne.). Siis
|
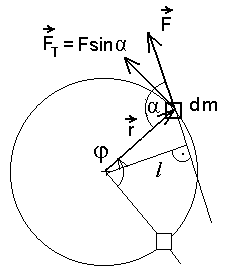
Tükikesele 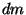 mõjuv jõud mõjuv jõud 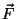 paneb pöörduma terve keha; arvesse tuleb vaid selle komponent paneb pöörduma terve keha; arvesse tuleb vaid selle komponent 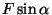 , mis mõjub piki rakenduspunkti liikumissuunda (trajektoori puutujat). , mis mõjub piki rakenduspunkti liikumissuunda (trajektoori puutujat).
|
kus 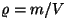 on tihedus ning integraal võetakse üle kogu
ruumala ning on tihedus ning integraal võetakse üle kogu
ruumala ning 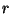 on tükikese on tükikese 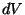 kaugus teljest. kaugus teljest.
Integraali saab arvutada korrapäraste kehade, nagu pöördkehad,
vardad, tasapinnalised plaadid jne. puhul, kui õnnestub iga tükikese
ruumala anda tema kauguse 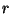 ja selle lõpmata väikese muudu ja selle lõpmata väikese muudu 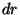 kaudu. Kõigil muudel juhtudel peame inertsimomendi määrama
katseliselt, pannes keha kindla jõu(momendi) abil pöörlema.
kaudu. Kõigil muudel juhtudel peame inertsimomendi määrama
katseliselt, pannes keha kindla jõu(momendi) abil pöörlema.
Kuidas seda teha? Vihje: meenutage üht laboritööd!
Milline on jõumoment ja kuidas ta tekib, on omaette probleem.
Koolifüüsikas käsitletakse lihtsaimat juhtu - jõupaari, mis
moodustub kahest vastassuunalisest, kuid piki erinevaid sirgeid
mõjuvast jõust. Tegelikult kujuneb jõumoment väga erinevat tüüpi
jõudude koosmõjul - olgu näiteks laboritöös trumlilt mahakeriv nöör
(mille poolt tekitatava jõumomendi suurust on lihtne
määrata), aga ka hüdro- või auruturbiinile ning elektrimootori
rootorile mõjuvad jõumomendid. Kõiki neid mõjusid saab võrrelda
lihtsalt ette kujutatava momendiühiku njuutonmeetriga.
|
Jõumoment on võrdeline jõuvektori mooduliga ning jõu mõjumissirge kaugusega pöörlemisteljest.
|
|
Njuutonmeeter (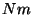 ) on jõumoment (pöördemoment), mis on
ekvivalentne ühenjuutonilise jõu poolt tekitatava momendiga, kui jõu
õla pikkus on üks meeter.
Jäiga keha pöörlemist iseloomustavate suuruste - jõumomendi
ning inertsimomendi - sisse toomine lubab kasutada pöördliikumise
kirjeldamiseks kulgliikumise valemeid. Paraku ei tee see neid
liikumisi sarnasemaks. Kui ühtlane sirgliikumine on vaba oma
olemuselt (keha jagunemisel osadeks jätkavad need kõik liikumist oma
esialgsetel trajektooridel); siis pöörlemisel püsivad keha osakesed
oma ringikujulistel trajektooridel ainult tänu keha koos hoidvatele
sisejõududele. Kui tükkideks jaguneb ühtlaselt pöörlev keha, lendavad
selle tükid mööda ruumi laiali. ) on jõumoment (pöördemoment), mis on
ekvivalentne ühenjuutonilise jõu poolt tekitatava momendiga, kui jõu
õla pikkus on üks meeter.
Jäiga keha pöörlemist iseloomustavate suuruste - jõumomendi
ning inertsimomendi - sisse toomine lubab kasutada pöördliikumise
kirjeldamiseks kulgliikumise valemeid. Paraku ei tee see neid
liikumisi sarnasemaks. Kui ühtlane sirgliikumine on vaba oma
olemuselt (keha jagunemisel osadeks jätkavad need kõik liikumist oma
esialgsetel trajektooridel); siis pöörlemisel püsivad keha osakesed
oma ringikujulistel trajektooridel ainult tänu keha koos hoidvatele
sisejõududele. Kui tükkideks jaguneb ühtlaselt pöörlev keha, lendavad
selle tükid mööda ruumi laiali.
Küsimus: Kas oskate leida jõumomenti juhul, kui jõud ei ole risti pöörlemisteljega?
|
Pöörlemise põhivõrrand:
Keha nurkkiirendus on võrdeline jõumomendiga
ning pöördvõrdeline inertsimomendiga.
|
Pöörlemisintegraalid. Pöördliikumisele saab
kerge vaevaga üle kanda ka töö, energia ja liikumishulga mõisteid.
Vastavad valemid
Suurust 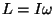 nimetatakse pöördimpulsiks, ka
pöörlemishulgaks ja impulssmomendiks. Siin on nad toodud
"lõpmata väikese ainetükikese" kohta - aga, nagu dünaamika
valemiski, saab neid summeerida-üldistada lõplike mõõtmetega keha
jaoks. nimetatakse pöördimpulsiks, ka
pöörlemishulgaks ja impulssmomendiks. Siin on nad toodud
"lõpmata väikese ainetükikese" kohta - aga, nagu dünaamika
valemiski, saab neid summeerida-üldistada lõplike mõõtmetega keha
jaoks.
|
Ka pöördliikumisel kehtivad liikumishulga ning kineetilise energia jäävuse seadused. Neid on mõistlik esitatada pöörlemisele sobivas formalismis, ehkki sisu on sama mis kulgliikumisel
|
Ja loomulikult kehtivad nende kohta kõik kulgliikumises õpitud
seadused. Kui pöörlemise kineetiline energia lihtsalt liitub
varasema, potentsiaalset ja kulgliikumise kineetilist energiat
sisaldava avaldisega, siis pöördimpulsi jäävuse seadust peetakse
täiesti iseseisvaks liikumisintegraaliks. Ikka selsamal põhjusel et
pöörlemine ja kulgliikumine pole samastatavad.
Pöörlemisvektorid. Lisaks ülaltoodule eristab
pöördliikumist kulgliikumisest erilise punkti -
pöörlemistsentri ja erilise sirge -pöörlemistelje olemasolu.
Nii jõu- kui inertsimoment sõltuvad pöörlemistsentri ning -telje
valikust. Kui vaadelda pöörlevat keha meie tavalises taustsüsteemis
(Cartesiuse ristkoordinaadistikus), on pöörlemistsenter määratud
kohavektoriga (nimetame seda pöörleva keha asukohaks ruumis),
pöörlemistelg aga sellest punktist lähtuva sirge -
pöörlemisvektoriga.
Pöörlemisvektoriga saab edasi anda kogu pöörlemisvõrrandi. Selleks
defineerime kolm suurust:
- pöördenurga vektor
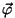 on vektor, mille moodul võrdub
pöördenurgaga ja mille suund antakse piki pöörlemistelge nii, et keha
pöördumisel ümber telje kehtiks "parema käe kruvireegel": on vektor, mille moodul võrdub
pöördenurgaga ja mille suund antakse piki pöörlemistelge nii, et keha
pöördumisel ümber telje kehtiks "parema käe kruvireegel":
- Kui keha pöörlemissuund võtta tavalise (parempoolse
vindiga) kruvi pöördumissuunaks, siis ühtib kruvi liikumissuund
pöördenurga vektori suunaga.
- nurkkiiruse vektor
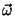 on vektor, mille moodul võrdub
nurkkiirusega ning mille suund piki telge ühtib pöördenurga suunaga,
kui nurk suureneb ja on sellega vastassuunaline, kui pöördenurk
väheneb; on vektor, mille moodul võrdub
nurkkiirusega ning mille suund piki telge ühtib pöördenurga suunaga,
kui nurk suureneb ja on sellega vastassuunaline, kui pöördenurk
väheneb;
- nurkkiirenduse vektor
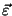 on vektor, ... (jätkake ise!). on vektor, ... (jätkake ise!).
|
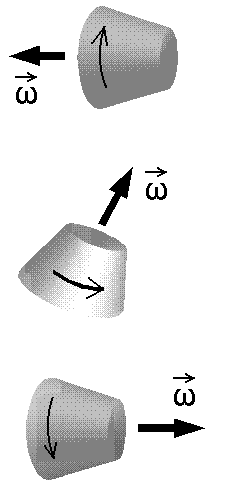
Pöörlemisvektorite suuna määrab (parempoolse) kruvi reegel.
|
|
Pöörlemisvektorid pole tegelikult õiged vektorid: neid ei saa
liita-lahutada, ka ei kehti nende jaoks taustsüsteemi vahetuse
valemid. Neid detaile käsitleb jällegi teoreetiline mehaanika. Et
märkida erinevust "õigete vektoritega", nimetatakse neid aksiaal- ehk
pseudovektoriteks.
Aga arvutada nendega saab. Näiteks võime pöörleva keha mingi punkti
joonkiiruse (tangentsiaalkiiruse) vektori avaldada nurkkiiruse
vektori ning vaadeldava keha kohavektori ja pöörlemistsentri
kohavektori vahe vektorkorrutisena:
kus 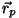 on vaadeldava punkti kohavektor, on vaadeldava punkti kohavektor, 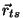 aga
pöörlemistsentri kohavektor. Mida kujutab endast vektorkorrutis,
vaadake matemaatika konspektist. aga
pöörlemistsentri kohavektor. Mida kujutab endast vektorkorrutis,
vaadake matemaatika konspektist.
Samasugused valemid saame teha ka pöörleva keha suvalise punkti nihke
ning tangentsiaalkiirenduse tarbeks. Tehke seda! Kuidas leida
normaalkiirendust, sellest järgmises punktis.
|
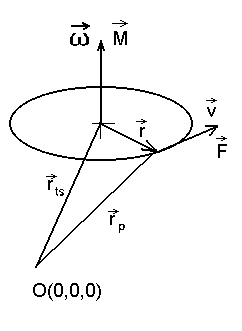
Punkti joonkiiruse leidmine keha nurkkiiruse ja tema ning pöörlemistsenri kohavektorite kaudu.
|
Inertsijõud pöörlevas süsteemis. Keha pöörlemine ei
tähenda midagi, iga tema "tükike" liigub ikkagi Newtoni
(kulgliikumise) seaduste järgi. Ringjoonelisel trajektooril hoiavad
teda aine ehitusest tulenevad sisejõud. "Tükikeste" püüdu
sirgliikumise poole kajastavad inertsijõud, mis on
tasakaalustatud sisejõudude poolt. Kõik nad tuletatakse Newtoni II
seadusest kujul
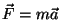 , kus kiirendus , kus kiirendus 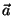 väljendab
"tükikese" vastuseisu pöörlemisest tekitatud trajektoori muutustele.
Neid viimaseid on kolme liiki: väljendab
"tükikese" vastuseisu pöörlemisest tekitatud trajektoori muutustele.
Neid viimaseid on kolme liiki:
- tsentrifugaaljõud on jõud, mis tasakaalustab
ringjoonelisel trajektooril liikuva keha normaalkiirenduse. Et
normaalkiirendus kutsub esile trajektoori kõverdumise ning sõltub
keha kiirusest, on tema suurus võrdeline nurkkiiruse ruuduga:
- Coriolise jõud tekib siis, kui mingi "tükike" peab
pöörleva keha (näiteks Maakera) pinnal või sees liikuma. Et keha
püüab oma tangentsiaalkiirust säilitada, tuleb teda pidurdada (kui
liikumine on suunatud telje poole) või kiirendada (kui keha liigub
teljest eemale. Tekib liikumisega risti olev inertsijõud.
|
Pöörlemisvektori praktilisi rakendusi:
a) pöörleva keha mingi punkti joonkiiruse 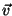 leidmine: leidmine:
b) jõumomendi 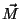 leidmine: leidmine:
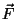 on jäiga keha punkti on jäiga keha punkti 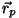 rakendatud jõud, rakendatud jõud,
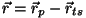 jõu rakenduspunkti ning pöörlemistsentri kohavektorite vahe. jõu rakenduspunkti ning pöörlemistsentri kohavektorite vahe.
|
- güroskoopilised jõud tekivad, kui püütakse muuta
pöörlemistelje ruumilist orientatsiooni. Nagu eelmiste jõudude korral
viib ka telje pööramine "tükikste" trajektoori muutmisele. Et igale
tükikesele vastab teisel pool telge samasugune, kuid vastassuunas
liikuv tükike, tekib siin inertsijõudude paar (seepärast ongi
need jõud mitmuses!), mis püüab telge "õigeks" pöörata. Kui keha
pöördimpulss on suur ja jõud väike, jääb tema mõju märkamatuks:
pöörlev keha säilitab oma ruumilise orientatsiooni. Kui jõud on suur,
hakkab keha pretsesseerima - tema telg pöördub ruumis, aga
mitte mõjuvate jõudude suunas, vaid nendega risti.
Tehnoloogias on olulised tsentrifugaal- ja güroskoopilised
jõud, kuna nende mõju seab piiranguid pöörlevate masinaosade
ehitusele. Põhjalikumalt tutvute nendega mehaanika kursuses.
|
Pöörleva keha käitumise määravad inertsijõud, mille tekkepõhjuseks on Newtoni I seadus - keha osade püüd säilitada ühtlast sirgjoonelist liikumist.
|
Pöörlemise tüübid. See, millest siiani juttu,
võiks kanda nime "pöörlemine teljel". Me oletasime, et pöörlemistelg
on ette määratud ning kõik meie pöörded toimusidki selle kindla telje
ümber. Polegi väga vale, kuna enamikus tehnilistest seadmetest on
pöörlemistelg fikseeritud võlli või laagrite abil.
Veeremine. Loodus ei tunne ei võlli ega ratast - mõlemad on
inimese väljamõeldis. Küll aga esineb looduses - ja üsna tihti -
nähtus, mida nimetatakse veeremiseks. Veerev keha liigub üheaegselt
nii pöörlevalt kui kulgevalt, seejuures jääb tema toetuspinnaga
kokkupuutev osa viimase suhtes paigale. Veeremise abil ületab loodus
hõõrdejõudu: takistus veeremisel puudub, kuna pindade omavahelist
nihkumist ei toimu.
Kui veerev keha on telgsümmeetriline (ratas, silinder, kera), liigub
pöörlemistelg kulgevalt, toetuspinnaga kokkupuutes olev osa seisab
(toetuspinna suhtes) paigal, selle vastaspunkt aga liigub teljega
võrreldes kahekordse kiirusega. Kui arvutada sellise veereva objekti
kineetilist energiat või liikumishulka, ei tohi unustada ka
pöörlemist. Näiteks saame veereva silindri kineetiliseks energiaks
|
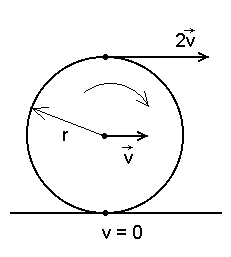
Veeremine: ratta alumine punkt seisab tee suhtes paigal, ülemine liigub kahekordse kiirusega.
|
ning arvestades, et silindri puhul 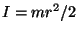 ja ja 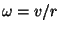 , ,
|
Veeremine: keha kulgliikumise kiirus v on võrdne veereva keha raadiuse r ja pöörlemiskiiruse 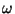 korrutisega. korrutisega.
|
|
Analoogiliselt arutledes saame liikumishulgaks
- aga arvutage parem ise. Ja püüdke välja mõelda, mis saab
liikumishulgast kui vektorist.
Ning veel üks küsimus: kumb veereb mäest alla kiiremini, kas ühtlase
tihedusega monoliitne silinder või õõnessilinder?
|
|
Vaba keha pöörlemine. Kuidas hakkab aga pöörlema keha, mis
pole kusagilt kinnitatud ega toetu ka pinnale? Näiteks sputnik,
lennuk või helikopter.
Et keha hakkaks pöörlema, peab teda mõjutama jõupaar - kaks
vastassuunalist võrdset jõudu, mis ei mõju piki sama sirget. Kõige
lihtsam on teha rida katseid, visates õhku näiteks risttahuka ja
pannes ta samal ajal pöörlema. Juhime tähelepanu kolmele faktile:
- Pöörlemine ei sõltu sellest, kas jõupaar rakendub
telje suhtes sümmeetriliselt või mitte;
- Vaba keha pöörlemistelg läbib alati masskeskme;
- Stabiilne pöörlemine on võimalik ainult kõige pikema või
kõige lühema telje ümber.
Ka selle kohta on teooria. Ükskõik missuguse kujuga keha jaoks saab
arvutada nn. inertsiellipsoidi - kolmeteljelise ühtlase
ainejaotusega ellipsoidi, mille inertsimomendid ükskõik millise
(masskeset läbiva!) telje suhtes on võrdsed modelleeritava keha
inertsimomendiga sama telje suhtes. Selle ellipsoidi kolm peatelge
määravadki vaba keha stabiilse pöörlemise oleku: keha saab pöörelda
vaid nende kahe telje ümber, mille suhtes tema inertsimoment on kas
minimaalne (mudelellipsoidi pikim telg) või maksimaalne (lühim telg).
Kui sundida vaba keha pöörlema mõne teise telje ümber (rakendades
vastava suunaga jõupaari), võtab keha pärast mõningat laperdamist
ruumis orientatsiooni, kus pikim/lühim telg on pööratud paralleelseks
pöörlemist esile kutsuva jõupaari momendivektori
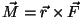 suunaga. suunaga.
|
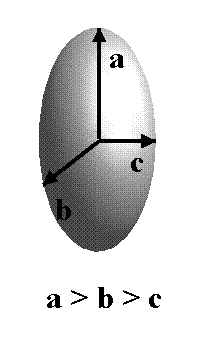
Inertsiellipsoid: pikima telje a suhtes on inertsimoment minimaalne, lühima telje c suhtes maksimaalne.
|
|
Miks nii, kuulub teoreetilise mehaanika kõrgema pilotaazi
valdkonda. Võite edasi mõelda. Annan ka vihje: lahendus peitub
(potentsiaalse?) energia miinimumi lauses ja (pöörd)impulsi jäävuse
seaduses. Keha lihtsalt ei saa teisiti pöörelda.
Väga kasulik seadus. Selle abiga stabiliseeritakse kosmilisi
sidesatelliite.
Kokkuvõtteks: pöörlev liikumine on äärmiselt keeruline, kõigi
üksikasjade suhtes puudub füüsikutel tänaseni üksmeel. Et ta on
samal ajal nii looduses kui tehnikas väga levinud, tuleb tema kohta
käivaid teooriaid võtta täie tõsidusega.
| Stabiilne pöörlemine on võimalik vaid nende pöörlemistelgede korral, kus pöörlemise kineetiline energia on antud pöörlemiskiiruse juures ekstremaalne.
|