|
Loeng 4. Töö ja energia.
Liikumisvõrrandi lahendamisel esile kerkivad probleemid sunnivad
tähelepanu pöörama liikumisele kui keha oleku muutusele. On selge, et
liikumine võib toimuda ka ilma jõudude (st. teiste kehade) abita. See
ühtlane sirgliikumine tähendab Newtoni I seaduse kohaselt aga mitte
oleku muutust, vaid kindlat oleku liiki (... säilitab oma
oleku kas paigalseisu või ühtlase sirgjoonelise liikumise kujul ...).
Ja niisama selge on see, et ükskõik kui suure jõu mõju ei suuda muuta
keha olekut - kuni puudub liikumine.
Järelikult tähendab oleku muutumine liikumise muutumist jõudude
mõjul. Selle muutuse ulatuse mõõtmiseks on füüsikutel eriline suurus
-- töö:
|
Oleku muutust saab mõõta protsessi iseloomustava suuruse - töö abil.
|
|
TÖÖ on keha liikumisoleku muutumise mõõt, mis on võrdne
keha poolt läbitud tee pikkuse ning kehale mõjuva jõu
liikumissuunalise komponendi korrutisega.
|
Töö arvutamisel läheb arvesse ainult jõu liikumissuunaline komponent, kuna just selle (komponendi) mõjul toimub oleku muutus.
|
|
Juhime tähelepanu sellele, et töö ei ole mitte
olekut (näiteks
liikumist), vaid selle muutumist kirjeldav suurus. Seega ei
iseloomusta ta mitte keha, vaid protsessi.
Töö on protsessi
kirjeldav parameeter.
Töö ühik ja mõõtmine. Et tee pikkuse ühikuks on
meeter (m) ja jõu ühikuks njuuton (N), peaks töö ühikuks sobima nende
korrutis. Nii see ka on, ja valemi lihtsuse huvides on jällegi võetud
ühik nii, et mingeid täiendavaid kordajaid ei tule:
Töö ühikuks on dzaul (J), mis on võrdne tööga, mida teeb
liikumissuunaline jõud üks njuuton tee pikkusel üks meeter.
Seega on ühe dzauli dimensiooniks
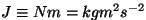
Nimetus on antud inglise füüsiku James Joule (1818 - 1889) järgi.
Tema nimelisi seadusi õpime hiljem.
|
Töö ühikuks SI süsteemis on dzaul,
tähis J,
dimensioon kg m2s-2.
|
|
Töö arvutamine. Definitsiooni järgselt tuleb töö
leidmiseks projekteerida kehale mõjuv jõud tema liikumise suunale
ning seejärel korrutada asendi muutuse - nihkega. Mõlemad (nii jõud
kui nihe) on vektorid. Töö seevastu on selgelt suunatu, st.
skalaarne suurus. Pole võimalik ju öelda, mis suunas tööd
tehakse.
Koolifüüsika töö valemiks on
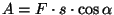 . Kui sellest
valemist pilt teha, näeme, et ta kehtib sirgliikumisel, kui jõud . Kui sellest
valemist pilt teha, näeme, et ta kehtib sirgliikumisel, kui jõud
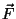 mõjub liikumissuunaga nurga all. Põhimõtteliselt saame
hakkama ka ilma koosinuseta, võttes "tee pikkuse" mõjub liikumissuunaga nurga all. Põhimõtteliselt saame
hakkama ka ilma koosinuseta, võttes "tee pikkuse" 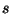 asemel
nihkevektori asemel
nihkevektori
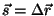 . .
Nii tekib korrektne valem
kus
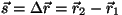 ning ning
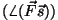 tähistab vektorite vahelist nurka.
tähistab vektorite vahelist nurka.
Töö valemis rakendame vektoralgebrast tuntud tehet - vektorite
skalaarkorrutist. Kui see koordinaatidesse ümber panna, saame väga
mugava valemi:
mis kahjuks kehtib vaid sirgliikumise ja muutumatu jõu korral.
Kui
liikumine on kõverjooneline või kui jõud muutub, kehtib see valem
üksnes lõpmata väikesel nihkel 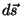 . Et leida tööd mingi pikema
liikumise korral, tuleb võtta integraal: . Et leida tööd mingi pikema
liikumise korral, tuleb võtta integraal:
Valem näib lihtne, aga ei ole seda. Me ei tohi sulge avada, sest tegu
pole "tavalise" määratud integraali, vaid joonintegraaliga. See
tähendab, et integreerimine toimub piki kindlat joont, milleks
mehaanikaülesannetes on trajektoori lõik punktist 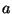 punktini punktini 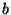 . .
Need punktid asuvad ruumis ja neil on samuti kolm koordinaati
(kohavektori komponendid). Kui valida teistsugune trajektoor, saame
integraalile tavaliselt ka teistsuguse väärtuse. Ja jõuvektori
komponendid 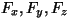 on kõik ruumi ja aja funktsioonid. on kõik ruumi ja aja funktsioonid.
Kuidas seda integraali siis arvutada? Kui on teada keha
liikumisvõrrand 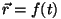 , saame kõik integraali all olevad
muutujad anda aja funktsioonidena, taandades joonintegraali
tavaliseks ühemõõtmeliseks (määratud) integraaliks. , saame kõik integraali all olevad
muutujad anda aja funktsioonidena, taandades joonintegraali
tavaliseks ühemõõtmeliseks (määratud) integraaliks.
Kui tahaksime
teha näiteks arvutiprogrammi, siis tuleks iga ajahetke jaoks leida
keha asukoht (liikumisvõrrandist) ja jõu valemi
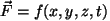 abiga arvutada jõu kolm komponenti. Seejärel korrutame neid vastavate
koordinaatide muutudega
abiga arvutada jõu kolm komponenti. Seejärel korrutame neid vastavate
koordinaatide muutudega
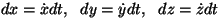 . Ja
alles siis võib integraali anda kolme eraldi integraali summana -
kusjuures nad kõik on integraalid aja, mitte koordinaatide
järgi.
Matemaatikud nimetavad seda "joonintegraali viimiseks
parameetrilisele kujule". Parameetriks on aeg - nagu
liikumisülesannetes ikka. . Ja
alles siis võib integraali anda kolme eraldi integraali summana -
kusjuures nad kõik on integraalid aja, mitte koordinaatide
järgi.
Matemaatikud nimetavad seda "joonintegraali viimiseks
parameetrilisele kujule". Parameetriks on aeg - nagu
liikumisülesannetes ikka.
|
Töö arvutus
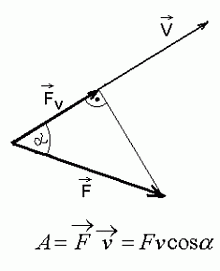
a) sirgjoonelisel liikumisel
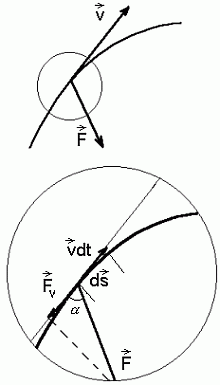 b) kõverjoonelisel liikumisel
b) kõverjoonelisel liikumisel
|
|
Kordamise huvides: mida kujutavad endast
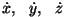 ? ?
| |
|
Võimsus ja kasutegur
Tehnilistes ülesannetes pole tihti tähtis mitte niivõrd mehhanismi poolt tehtud töö, kui töövõime. Sellistel juhtudel arvutatakse keha poolt ajaühiku kohta tehtav töö, mida nimetatakse võimsuseks:
| |
Võimsus on keha (kehade süsteemi, mehhanismi) töövõimet iseloomustav suurus, mis on võrdne ajaühiku kohta tehtava tööga.
Võimsuse ühikuks on vatt (tähis W). Üks vatt vastab võimsusele, kus sekundis tehakese üks dzaul tööd.
Ühik on nimetatud 1784. a. esimese kasutuskõlbliku aurumasina konstrueerinud inglise leiduri James Watt'i järgi.
Seniõpitud suurustest sarnaneb võimsus kõige rohkem kiirusele (ajaühiku kohta läbitud tee pikkus). Ja nagu kiirust saab ka võimsust arvutada tuletisena aja järgi:
|
Töö tuletist aja järgi nimetatakse võimsuseks
Võimsus iseloomustab töötavat seadet ja väljendab selle poolt ajaühikus tehtavat tööd
Võimsuse ühikuks SI süsteemis on vatt,
tähis W,
dimensioon kg m2s-3.
|
Selliselt arvutatud võimsust nimetatakse hetkvõimsuseks. Kasutatakse ka keskmist võimsust (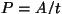 ), nimivõimsust ja maksimaalselt lubatavat võimsust. Viimased kaks on juba tehnikaalased terminid. ), nimivõimsust ja maksimaalselt lubatavat võimsust. Viimased kaks on juba tehnikaalased terminid.
Kasulik töö, kogu töö, kasutegur. Looduses ja tehnikas on jõudusid, mille tehtud töö ei muutu mehaaniliseks energiaks, vaid "läheb kaotsi" (tavaliselt muutub soojuseks). Selliseid jõudusid nimetataks mittekonservatiivseteks (energiat mitte säilitavateks) ja nende näiteks
on hõõrdejõud ja takistusjõud. Kui soovime leida töö valemi abil energiamuutust (või energia jäävuse seaduse abil tööd), tuleb mittekonservatiivsete jõudude töö vaatlusest välja jätta. Kõige lihtsam on seda teha kasuteguri abil:
Seadme kasuteguriks nimetatakse samas ajavahemikus tehtud kasuliku (energiat muutva) töö ja kogu tehtud töö suhet.
Et ajaühikus tehtud töö kannab nimetust "võimsus", saab kasuteguri avaldada ka võimsuste suhtena. Kokku saame ilusa valemite komplekti:
Mida kujutas endast kaotsi läinud "mittekasulik" töö, meid neis valemites enam ei huvita.
|
Seadme efektiivsust iseloomustab kasutegur
Kasutegur väljendab kasuliku töö ja kogutöö (kulutatud energia, kütuse jms) suhet. Teda võib arvutada ka kui võimsuste suhet.
Kasutegur on dimensioonita suurus. Tavaliselt antakse ta protsentides.
|
|
Energia kui olekuparameeter. Niisiis väljendab
töö keha (liikumis)oleku muutust. Oleks loomulik, kui seda "olekut"
saaks kirjeldada samuti mingi suurusega, mis on tööga samanimeline ja
mis töö käigus muutub. Selliseks suuruseks on energia:
Energia on keha olekut kirjeldav suurus, mille muut on
võrdne ja vastasmärgiline selle keha poolt tehtava tööga.
|
Energia iseloomustab keha olekut oleku muutmiseks tehtava töö kaudu.
Teda mõõdetakse samades ühikutes kui töödki.
|
Niisiis:
- kui keha teeb tööd, tema energia väheneb.
- Kui tööd
teevad teised kehad (mille mõju on keha poolt avaldatava jõuga
vastasmärgiline), energia suureneb.
| |
Kineetiline energia. Vaatleme lihtsaimat juhtu, kus kehale
massiga 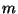 mõjub konstantne jõud mõjub konstantne jõud 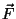 . Et asi veel lihtsam
oleks, võtame sellise taustsüsteemi, kus keha hetkel . Et asi veel lihtsam
oleks, võtame sellise taustsüsteemi, kus keha hetkel 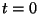 on paigal
( on paigal
(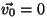 ). Selline keha hakkab liikuma sirgjooneliselt
(mitteühtlaselt, kiirus kasvab!) ja hetkeks ). Selline keha hakkab liikuma sirgjooneliselt
(mitteühtlaselt, kiirus kasvab!) ja hetkeks 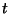 on tema kiirus: on tema kiirus:
Kiiruse muutus tähendabki oleku muutust: olek hetkel 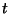 erineb
olekust hetkel erineb
olekust hetkel 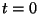 selle poolest, et keha liigub nüüd kiirusega selle poolest, et keha liigub nüüd kiirusega
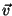 . .
Arvutame nüüd jõu 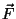 poolt ajavahemiku poolt ajavahemiku 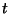 jooksul tehtud töö.
Et liikumine oli jõu mõjumissuunas, on vektorite vaheline nurk null
ja selle koosinus 1. Järelikult on töö jooksul tehtud töö.
Et liikumine oli jõu mõjumissuunas, on vektorite vaheline nurk null
ja selle koosinus 1. Järelikult on töö 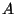 võrdne jõu võrdne jõu 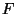 ja läbitud
tee pikkuse ja läbitud
tee pikkuse 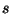 korrutisega. Viimase leiame valemist korrutisega. Viimase leiame valemist
ja töö
|
Tähelepanu! - nii töö kui energia väärtused sõltuvad taustsüsteemist!
Üleminekul teise, esialgse suhtes liikuvasse taustsüsteemi ei saa töö ja energia väärtusi üle kanda. Nad tuleb uuesti arvutada ja nad kehtivad ainult vaadeldava süsteemi piires.
|
|
Suuruse 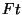 leiame kiiruse valemist: leiame kiiruse valemist:
ja asendame töö valemisse:
See töö kulus liikuma pandud keha energia suurendamiseks:
juhul, kui keha seisis enne jõu mõjuma hakkamist paigal.
| |
|
Leitud suurust 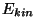 nimetatakse keha kulgeva liikumise
kineetiliseks energiaks.
Kui keha seisab (mingis taustsüsteemis!)
paigal, on tema kineetiline energia (selles süsteemis!) null. Mingis
teises süsteemis võib sama keha kineetiline energia nullist erineda,
sel juhul tingib välisjõu mõjumine energia muutumise.
Saab
näidata, et kui keha liigub algul näiteks kiirusega nimetatakse keha kulgeva liikumise
kineetiliseks energiaks.
Kui keha seisab (mingis taustsüsteemis!)
paigal, on tema kineetiline energia (selles süsteemis!) null. Mingis
teises süsteemis võib sama keha kineetiline energia nullist erineda,
sel juhul tingib välisjõu mõjumine energia muutumise.
Saab
näidata, et kui keha liigub algul näiteks kiirusega 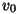 , on tehtud
töö võrdne kineetilise energia muutusega , on tehtud
töö võrdne kineetilise energia muutusega
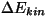 . Seda
isegi juhul, kui jõud on esialgse liikumissuunaga nurga all. . Seda
isegi juhul, kui jõud on esialgse liikumissuunaga nurga all.
|
Kineetiline energia on liikuva keha energia.
Et selle keha liikumist peatada, tuleb teha samapalju tööd, kui kulus keha liikuma panemiseks..
|
|
Tõestage seda! Võtke algkiiruseks 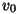 , mis on x-telje suunaline ja
pange jõud , mis on x-telje suunaline ja
pange jõud 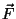 mõjuma sellega mõjuma sellega 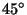 nurga all. Leidke jõu nurga all. Leidke jõu
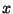 - ja - ja 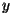 -komponendid, arvutage kiirendused ja seejärel
liikumisvõrrandist uus kiirus -komponendid, arvutage kiirendused ja seejärel
liikumisvõrrandist uus kiirus
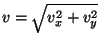 . .
Kui suudate
arvutada ka (kõverjoonelisel liikumisel!) tehtud töö, näete, et see
on täpselt võrdne kiirustele 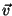 ja ja 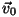 vastavate
kineetiliste energiate vahega. vastavate
kineetiliste energiate vahega.
Hoiatan: tegu on tõsise rehkendusega! Kel algebraga raskusi, võib
mingil momendil tähtede asemele numbrid panna.
| |
|
Potentsiaalne energia. Välisjõudude töö ei tarvitse alati
keha energiat suurendada. Ülesvisatud keha liikumisel mõjub talle
Maa külgetõmbejõud, mis aga ei suurenda, vaid hoopis vähendab keha
kiirust. Koos sellega väheneb ka keha kineetiline energia.
Kui üles visatud keha peatub, saab nulliks ka tema kineetiline
energia. See ei tähenda aga sugugi, et kogu energia nulliks
muutub. Sama keha kogub alla kukkudes uuesti kiirust ja tema
kineetiline energia kasvab sellesama Maa külgetõmbejõu mõjul.
Siit: liikumisenergia pole ainus (mehaanilise) energia liik. Keha
võib omada energiat ka oma asukoha tõttu teiste kehade suhtes. Üles
riputatud raskus, pingule keeratud vedru, veehoidla tammi taha
kogunenud vesi - kõik need omavad mingit energiavaru, mida
nimetatakse potentsiaalseks energiaks. Nagu kiiruse muutmiseks,
tuleb ka jõudude mõju all oleva keha asukoha muutmiseks teha tööd. Ja
nagu liikumise korralgi loetakse tehtud töö positiivseks, kui keha
energia kasvab ning negatiivseks, kui energia kahaneb.
Potentsiaalse energia muutumise valem sõltub jõudude tüübist.
Raskusjõu korral on üles tõstetavale kehale mõjuv jõud konstantne
(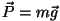 ) ning tehtav töö on võrdeline kõrguse muutusega
( ) ning tehtav töö on võrdeline kõrguse muutusega
(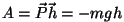 ), kuna raskusjõud ), kuna raskusjõud 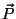 ning vertikaalnihe ning vertikaalnihe
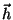 on vastassuunalised.
Vedru venitamisel kasvab elastsusjõud võrdeliselt venituse ulatusega
(deformatsiooni suurusega, on vastassuunalised.
Vedru venitamisel kasvab elastsusjõud võrdeliselt venituse ulatusega
(deformatsiooni suurusega,
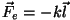 ) ning ) ning
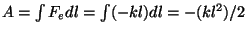 . .
|
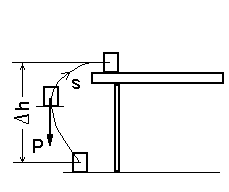
Keha liigutamisel ei sõltu raskusjõu töö liikumisteest, vaid ainult alg- ja lõpp-oleku kõrguste vahest.
|
|
Normeerimine. Toodud valemid näitavad keha
nihutamisel tehtud tööd. Juhime tähelepanu asjaolule, et kirja pandud
integraalid on antud määramata integraali kujul ja seepärast
peaks lõppvalem sisaldama aditiivset (juurde liidetavat)
integreerimiskonstanti 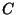 . Tegelikult on nihkel alati algus ja lõpp,
mis, kajastudes integreerimistee otspunktidena
( . Tegelikult on nihkel alati algus ja lõpp,
mis, kajastudes integreerimistee otspunktidena
( ), teeb määramata integraalist määratud
integraali. ), teeb määramata integraalist määratud
integraali.
Kui rääkida energiast, siis meie näidetes on sellelgi "normaalne",
valemist endast tulenev nullpunkt. Võttes üles tõstetava raskuse
potentsiaalse energia valemiks
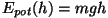 , saame energia
nullväärtuse punktis , saame energia
nullväärtuse punktis 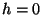 . Sama tuleb välja elastsusjõu valemist
( . Sama tuleb välja elastsusjõu valemist
(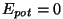 kui kui 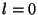 ). Kui mingi jõud on nihke või selle ruuduga
pöördvõrdeline (nagu gravitatsioonijõud), võime nullpunktiks
valida ka lõpmatuse. ). Kui mingi jõud on nihke või selle ruuduga
pöördvõrdeline (nagu gravitatsioonijõud), võime nullpunktiks
valida ka lõpmatuse.
Üldjuhul on normeerimine suvaline ja seetõttu
öeldakse, et potentsiaalne energia on määratud aditiivse
konstandi täpsusega.
Mida see tähendas? Ja kas suudate näidata, et sama lause
käib ka kineetilise energia kohta?
|
Energia nagu kõik määramata integraalid on määratud vaid konstandi täpsuseni. Selle konstandi leidmiseks peame teadma keha energiat mingil ajamomendil (või mingis kindlas punktis).
|
|
Märgiprobleem. Kui kineetilise energia avaldises oli kõik
selge - jõud mõjus liikumise suunas ja kuna tema poolt tehtav töö
suurendas liikuva keha energiat, pidigi märk olema positiivne. Ja kui
jõud juhtus mõjuma liikumisele vastassuunas, tuli märk negatiivne
ning kuna keha kiirus vähenes, vähenes ka liikuva keha (kineetiline)
energia.
Potentsiaalse energia korral tundub olevat vastupidi: kui nihe on jõu
suunaga vastupidine (raskust tõstetakse ja vedru venitatakse vastu
jõu mõjumissuunda), siis potentsiaalne energia kasvab. Ning kui
raskust allapoole või vedru lõdvemale lasta, energia väheneb (kuigi
liikumine toimub jõu mõjumise suunas).
|
Kui jõud mõjub liikumise suunas, siis potentsiaalne energia väheneb, kineetiline aga kasvab.
Kui jõud mõjub liikumisele vastassuunas, siis kineetiline energia kahaneb, potentsiaalne aga kasvab.
|
|
See ongi potentsiaalse energia märgiprobleem. Kui keha
(süsteem) osutab talle mõjuvale jõule vastupanu, salvestub selle
jõu vastu tehtud töö potentsiaalse energiana. Et potentsiaalne
energia saaks kasvada, peab lisaks raskus- või elastsusjõule kehale
mõjuma veel mingi vastassuunaline välisjõud. Potentsiaalse
energia omapära ongi selles, et ta ei kehti kunagi üksiku
keha, vaid kehade süsteemi kohta. Sellesse süsteemi kuuluvate
kehade vahel mõjuvaid jõude nimetame sisejõududeks, süsteemi
kehadele väljaspoolt mõjuvaid aga välisjõududeks.
Potentsiaalse
energia muutumist võivad esile kutsuda mõlemad, kuid:
süsteemi potentsiaalse energia suurenemine on võimalik üksnes
välisjõudude töö arvelt.
| |
|
Nüüd peaks paistma ka märgiprobleemi lahendus: nii, nagu pole
võimalik vedru pikenemine elastsusjõu arvel ei saa ka kehasid tõsta
raskusjõu arvel. Mõlemad on sisejõud ja selleks et vedru hakkaks
pikenema (keha ülespoole tõusma), peab talle mõjuma välisjõud, mis on
vastassuunaline (vektorformalismis vastasmärgiline) nimetatud
(sise)jõududega. Kui raskusjõu töö keha tõstmisel on negatiivne, siis
temaga vastassuunalise välisjõu töö on loomulikult positiivne - ja
just selle (välis)jõu töö suurendabki süsteemi potentsiaalset
energiat.
|
Potentsiaalse energia märk valitakse vastavalt ülesande iseloomule.
|
|
Miks me siis üldse kasutame potentsiaalse energia valemis
sisejõudusid? Võiks ju panna kohe valemisse vedru venitava välisjõu
ning probleem oleks olematu!
Paraku pole see võimalik. Kui välisjõud oleks täpselt võrdne
sisejõuga, oleks jõud tasakaalus ja mingit venitamist ei toimuks.
Selleks, et vedru hakkaks pikenema (keha kerkima), peab välisjõud
olema suurem sisejõust. Kui palju, pole oluline - ja enamikul
juhtudest pole see ka täpselt määratav. Ja ainult osa selle
välisjõu tööst kulub potentsiaalse energia suurendamiseks. Ülejäänu
kas suurendab keha kiirust (kasvatades kineetilist energiat) või
läheb kaotsi hõõrdumise ja õhutakistuse ületamisel. Täpselt on
määratav ainult sisejõu ületamiseks kulunud töö ja seda kirjeldasidki
ülaltoodud valemid.
Järelikult on potentsiaalse energia muut vastasmärgiline kehale
mõjuva sisejõu poolt tehtava tööga. Kui panna nii kineetilise
kui potentsiaalse energia muudu sõltuvus (välisjõudude poolt) tehtud
tööst kirja valemitena, peame potentsiaalse energia miinusmärgi
unustama, saades:
ja kogu tehtud töö
| |
kus
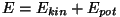 ehk, kasutades teoreetilise mehaanika
tavatähiseid, ehk, kasutades teoreetilise mehaanika
tavatähiseid,
Suurust 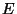 nimetatakse mehaaniliseks koguenergiaks,
teoreetilises mehaanikas ka Hamiltoni funktsiooniks. nimetatakse mehaaniliseks koguenergiaks,
teoreetilises mehaanikas ka Hamiltoni funktsiooniks.
|
Keha või süsteemi kineetilise ja potentsiaalse energia summat nimetatakse mehaaniliseks koguenergiaks.
|
Nagu
järgnevas näeme, lihtsustab energia mõiste kasutamine paljude
liikumisülesannete lahendamist. Muuseas - teoreetilises mehaanikas
kasutatakse ka energia-avaldise tüüpi, kus potentsiaalse energia märk
on muutmata. Saadud funktsiooni 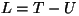 nimetatakse Lagrange'i
funktsiooniks e. lagranziaaniks, nii et palun mitte segi ajada. nimetatakse Lagrange'i
funktsiooniks e. lagranziaaniks, nii et palun mitte segi ajada.
Energia jäävuse seadus. on otsene järeldus
energia valemist. Kui "mehaanilise koguenergia muutus on võrdne
välisjõudude poolt tehtud tööga", siis sellest järeldub, et
välisjõudude töö puudumisel on koguenergia muutus null. Ja kui mingi
suuruse muutus on null, tähendab see, et vaadeldav suurus on
muutumatu e. jääv.
Konservatiivsed ja mittekonservatiivsed jõud. Enne kui
energia jäävuse seaduse kirja paneme, täpsustame tema kehtivuse
piire. Esiteks on lisaks välisjõududele olemas ka süsteemi kehade
vahel mõjuvad sisejõud, mille töö tulemusel võib energia samuti
muutuda.
Nimelt on olemas terve rida jõudusid, mille toimimise käigus
mehaaniline energia hajub, muutudes teisteks energialiikudeks -
näiteks soojus- või elektrienergiaks. Nii neid jõudusid ka
nimetatakse - mittekonservatiivseteks (ld. conservare --
säilitama), mõnikord ka dissipatiivseteks (ld. dissipatio --
hajuma, kaduma) jõududeks.
Tüüpilised mittekonservatiivsed jõud on
näiteks hõõrde- ja takistusjõud: nende poolt tehtav "töö" tähendab
igal juhul kaotsi läinud energiat. Linnasõidul on auto kütusekulu
alati suurem, kuna sagedased pidurdamised hajutavad liikumisenergiat.
Maanteel sõltub kütusekulu kiirusest, kuna õhutakistus on võrdeline
kiirusega. (Kiirustel üle 30 m/s e. 0.1 helikiirust hakkab takistus
kasvama isegi võrdeliselt kiiruse ruuduga, sellest ka suurenenud
kütuse kulunormid 120-kilomeetrise tunnikiiruse korral.)
Teine vajalik täpsustus puudutab "välisjõudude tööd", mille nulliga
võrdumine tähendab kas jõu või liikumise puudumist. Viimane neist on
liig suur piirang: kui ükski keha ei liigu, pole mõtet rääkida ka
oleku muutumisest (liikumisest). Järelikult piirdume jõudude kohta
käiva tingimusega. Kokku saame:
Süsteemis, mille sisejõud on konservatiivsed, on
välisjõudude puudumisel mehaaniline koguenergia jääv.
"Jääv" tähendab matemaatikas ja füüsikas protsessi vältel
muutumatut suurust; "konstantne" käib tavaliselt konkreetse seisundi
(oleku) kohta. Pole suur viga, kui neid lugeda sünonüümideks.
Ülesanne pidurdavast autost. Kui seaduses toodud tingimused
pole täidetud, annab energia jäävuse seadus äärmiselt praktilise
eeskirja paljude dünaamika ülesannete lahendamiseks:
Süsteemi mehaanilise energia muut võrdub välisjõudude
tehtud töö ning kõigi protsessis osalevate mittekonservatiivsete
jõudude poolt tehtava töö vahega
Kuidas seda valemit kasutada, selgub järgmisest näitest. Olgu meil
tavaline mehaanika ülesanne:
Milline peaks olema pidurdav jõud, et peatada kiirusega
108 km/h liikuv auto, mille mass on 1 t, 50 meetri piikusel lõigul?
Millise hõõrdeteguri korral on selline pidurdamine üldse võimalik?
Et praktikumis sai sellega juba vaeva nähtud, ei hakka me praegu
rassima Newtoni seadustega, vaid paneme kohe kirja energia jäävuse
seaduse:
millest leiame vahetult otsitavad suurused:
| |
Vapustav, aga mitte veel kõik. Kujutame ette, et pidurdamine toimub
mitte tasasel maal, vaid tõusul või langusel. Kui tahaksime nüüd
lähtuda Newtoni seadustest, tuleks meil vaadelda liikumist
kaldpinnal, jagada jõud komponentideks jne. Energia valemi abil saame
lihtsalt energia avaldisse täiendava liikme:
Lisaliige 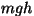 asub sulgudes, järelikult lisandub valemisse liige asub sulgudes, järelikult lisandub valemisse liige
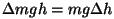 , kuna kolmest valemis olevast suurusest
muutub vaid kõrgus. Tavaliselt antakse
tee kalle protsentides; vaatame juhtu, kus pidurdamine toimub vastu
mäge, mille tõus on 5%. Matemaatiliselt tähendab see, et , kuna kolmest valemis olevast suurusest
muutub vaid kõrgus. Tavaliselt antakse
tee kalle protsentides; vaatame juhtu, kus pidurdamine toimub vastu
mäge, mille tõus on 5%. Matemaatiliselt tähendab see, et
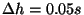 . Et pidurdamine toimub vastu mäge, kasvab selle käigus
potentsiaalne energia. Jõu valemiks saame: . Et pidurdamine toimub vastu mäge, kasvab selle käigus
potentsiaalne energia. Jõu valemiks saame:
Lahendus on vapustavalt lihtne. Proovimiseks arvutage, milline peaks
olema hõõrdetegur, kui soovime autot laskumisel pidama
saada.
|
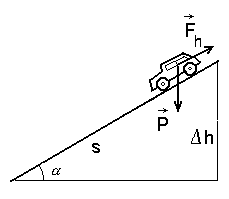
Auto pidurdamisel peab pidurdav jõud lisaks kineetilisele energiale kustutama ka langusele vastava potentsiaalse energia
E = 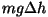 . .
|
|
Liikumisintegraalid. Tasub meelde jätta: alati,
kui liikumisülesandes küsitakse sõltuvust kehale mõjuva jõu ning tema
poolt läbitud tee pikkuse vahel, on kasulik rakendada energia jäävuse
seadust. Selle pärast, et töö on integraal jõust ja tee
pikkusest. See integraal on võrdeline liikumise käigus tekkiva
energiate vahega. Energia muutus (lõpp- ja algenergia vahe) on seega
liikumise integraalne (summeeruv) muutus ning seepärast võib energiat
nimetada liikumisintegraaliks. Nagu eelnevas ülesandes nägime,
aitab tema kasutamine vältida kiirenduse (kiiruse tuletise) leidmist.
Selle asemel, et töötada tuletistega, töötasime integraalidega.
Energia pole ainuke liikumisintegraal. Integreerides Newtoni II
seadust, saame:
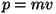 on keha impulss ehk liikumishulk. Kuna Newtoni II
seaduse (originaalformuleeringu) järgi toimub impulsi muutus jõu on keha impulss ehk liikumishulk. Kuna Newtoni II
seaduse (originaalformuleeringu) järgi toimub impulsi muutus jõu
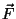 mõjumise suunas, kehtib saadud valem kõigi jõuvektori
komponentide, seega kogu jõuvektori kohta. mõjumise suunas, kehtib saadud valem kõigi jõuvektori
komponentide, seega kogu jõuvektori kohta.
Proovige ja te veendute, et ka see liikumisintegraal lubab kiiresti
ning kadudeta lahendada liikumisülesandeid. Seekord selliseid, kus
kasutatakse seost jõu 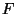 ning tema toimimisaja ning tema toimimisaja 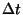 vahel. vahel.
Ja nagu energia, nii võime ka impulsi kohta anda jäävusseaduse. See
on siis impulsi jäävuse seadus.
Kui süsteemile mõjuvate välisjõudude summa on
null, on süsteemi kehade impulsside summa jääv suurus.
NB! Seaduses on rõhutatud, et oluline on üksnes välisjõudude
mõju. Millised jõud mõjuvad süsteemi kuuluvate kehade vahel, pole
seega oluline.
Kas suudate seda tõestada? Annan vihje: Newtoni II seaduse kohaselt
mõjuvad jõud ainult paariti ja seejuures vastassuunas. Mis järeldub
siit impulsside kohta?
| |