|
Dünaamika.
Sõnaga dünaamika (kr. dynamis - jõud) nimetatakse
mehaanika osa, mis kirjeldab kehade vahelise vastasmõju seost
liikumisega. Põhilise osa temast annavad erinevate vastasmõju liikide
(eri tüüpi jõudude) matemaatilise formuleerimise ning vastavate (teist järku!) diferentsiaalvõrrandite lahendamise probleemid.
Newtoni seadused. Klassikalise dünaamika aluseks
on kolm Newtoni poolt formuleeritud seadust. Newton oma 1687. a.
ilmunud teoses Loodusfilosoofia matemaatilised printsiibid
(Philosophiae naturalis principia mathematica) püüdis füüsikat
üles ehitada klassikalise geomeetria kombel, tuletades kõigi talle
teada olevate nähtuste kirjeldused kolmest põhipostulaadist.
Koolifüüsika formuleeringus oleksid need (nn. Newtoni seadused):
|
Dünaamika ülesandeks on:
- leida kehade vastasmõjule matemaatiline esitus;
- lahendada saadud diferentsiaalvõrrand
|
- Iga keha seisab paigal või liigub ühtlaselt sirgjooneliselt
kui talle ei mõju teised kehad või kui nende kehade mõjud
kompenseeruvad.
- Keha kiirendus on võrdeline talle mõjuva jõuga ning
pöördvõrdeline keha massiga.
- Kaks keha mõjutavad teineteist alati jõududega, mis on
suuruselt võrdsed ja suunalt vastupidised.
|
Newtoni seadused tuleb pähe õppida.
|
|
Et tegu on kogu füüsika seisukohalt äärmiselt olulise
momendiga, anname ka Newtoni originaal-formuleeringud:
- Iga keha säilitab oma oleku kas paigalseisu või ühtlase
sirgjoonelise liikumise kujul seni, kuni temale rakenduvad jõud seda
olekut ei muuda.
- Liikumishulga muutus on võrdeline kehale mõjuva jõuga ning
toimub samas suunas mõjuva jõuga.
- Jõud esinevad ainult paariti: iga mõjuga kaasneb alati niisama
suur, kuid vastassuunaline vastumõju.
|
NB! Newtoni II ja III seadus käsitlevad jõudu kui vektorit!
Matemaatikast:
Väide "suurus A on võrdeline suurusega B" tähendab seda, et neist ühe (näiteks A) suurendamine mingi arv korda toob endaga kaasa teise (B) suurnemise sama arv korda
|
|
Jõud, mass, liikumishulk. Jätkame keeleõpet. Jõud ja
liikumine on meil juba defineeritud, samuti mõiste "keha". Ära tuleb
seletada mass ja liikumishulk.
Mass on keha inertsuse mõõt; ta väljendub vastupanus
(liikumis)oleku muutumisele väliste jõudude toimel.
Liikumishulk e. impulss on (liikumis)olekut kirjeldav
suurus , mis defineeritakse kui keha massi ja liikumiskiiruse korrutis.
Nagu näeme, toetuvad mõlemad mõisted samale nähtusele -- kehade
inertsusele (ld. inertia -- loidus, laiskus) kui võimele säilitada
oma olek. Staatikas tulenes oleku muutumatus jõudude tasakaalust -
nii ka dünaamikas, puudub vaid paigalseisu nõue. Seega on dünaamika
seisukohalt tasakaaluolekuks ka ühtlane sirgliikumine, paigalseis
(kiiruse võrdumine nulliga) on üksnes selle erijuht.
| |
|
Mida see "mass" endast kujutab, on niisama mõttetu küsimus, kui
probleem aja või ruumi olemusest. Newtoni järgi on mass "ainehulga
mõõt, mis kujuneb võrdeliselt tiheduse ja ruumalaga". Selle "massi"
mõõtmiseks kasutati juba enne Newtonit kehade kaalumist, st.
aine hulga määramist temale mõjuva raskusjõu abil. Raskusjõud
(jõud, millega Maa tõmbab külge tema pinnal olevaid esemeid) on
millegipärast võrdeline täpselt sama massiga, mis läheb Newtoni teise
(inertsi)seadusesse.
| Mass on aja ja pikkuse (ruumilise ulatuse) kõrval kolmas mehaanika põhisuurus.
|
Kordan veel kord: füüsika ei seleta, vaid kirjeldab loodust.
Newtoni seadused, aga ka kõik järgnevas kursuses õpitav, on
loodusnähtuste matemaatiline kirjeldus. Selliseid kirjeldusi on ajaloo
jooksul tehtud igasuguseid, meie õpime ja kasutame vaid neid, mis on
ajaproovile vastu pidanud ja mis annavad kasulikke rakendusi.
Massi ühikuks on kilogramm (kg):
1 kilogramm on ühe kuupdetsimeetri
(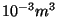 ) puhta vee mass temperatuuril ) puhta vee mass temperatuuril 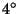 C ja rõhul
1.013 MPa.
Kilogrammi etalooniks on plaatinast silinder, mida
hoitakse Rahvusvahelise Kaalude ja Mõõtude Büroos Pariisis. Et
kaalumine - kaalude võrdlemine - on tehniliselt lihtsasti
korraldatav ja väga täpne mõõtmise liik, kasutatakse igapäevaelus
ainehulga määrajana just massi. C ja rõhul
1.013 MPa.
Kilogrammi etalooniks on plaatinast silinder, mida
hoitakse Rahvusvahelise Kaalude ja Mõõtude Büroos Pariisis. Et
kaalumine - kaalude võrdlemine - on tehniliselt lihtsasti
korraldatav ja väga täpne mõõtmise liik, kasutatakse igapäevaelus
ainehulga määrajana just massi.
| Mass on ainus tänapäeval kasutusel olev suurus, mille etalooniks on mitte arvutuseeskiri, vaid reaalne keha.
SI süsteemi ühikud jagunevad
- põhiühikud - siin meeter, sekund, kilogramm
- tuletatud ühikud - siin näiteks njuuton
Tuletatud suuruse dimensioon on tema avaldis põhiühikute kaudu.
|
|
Jõu ühik rahvusvahelises süsteemis SI on tuletatud Newtoni II
seadusest. Seadus ütleb, et kiirendus on võrdeline jõuga -
seega peaks valemis olema võrdetegur - konstantne kordaja, millega
korrutatakse jõu ja massi suhet. Kui valida jõu ühik nii, et
võrdetegur oleks võrdne ühega, saaksime lihtsaima valemi. Nii ka
toimitakse.
Jõu ühikuks on njuuton (N)
1 njuuton on jõud, mis annab ühe kilogrammise massiga
kehale kiirenduse üks meeter sekundis sekundi kohta.
Njuutoni dimensioon - väljend põhiühikute (meeter,
sekund, kilogramm) kaudu on 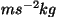 ehk ehk 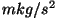 . .
|
Jõu ühik - njuuton - on nimetatud klassikalise mehaanika rajaja Isaac Newtoni nime järgi.
Reegel on, et selliste ühikute tähis algab suure tähega, nende eestikeelne nimetus aga kirjutatakse vastavalt originaalkeele hääldusele.
|
|
Liikumisvõrrand Newtoni mehaanikas. Tuletame
meelde: kinemaatikas tähendas liikumisvõrrand keha asukoha (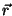 )
sõltuvust ajast. Seda sõltuvust võib väljendada ruutpolünoomina )
sõltuvust ajast. Seda sõltuvust võib väljendada ruutpolünoomina
kus 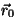 , , 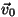 ja ja 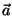 on konstantsed vektorid.
See
võrrand kujutab ühtlaselt muutuvat (kiirenevat või aeglustuvat)
liikumist (kuna kiirendusvektor on konstantsed vektorid.
See
võrrand kujutab ühtlaselt muutuvat (kiirenevat või aeglustuvat)
liikumist (kuna kiirendusvektor 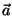 on konstantne).
Newtoni II seaduse kohaselt sõltub kiirendus kehale mõjuvast jõust,
mis omakorda võib olla ajas muutuv suurus. Võrrandist on konstantne).
Newtoni II seaduse kohaselt sõltub kiirendus kehale mõjuvast jõust,
mis omakorda võib olla ajas muutuv suurus. Võrrandist
|
Newtoni dünaamikas kasutatavad tähised:
- skalaarid:
- vektorid:
- s - nihe
- v - kiirus
- a - kiirendus
- F - jõud
- p - impulss, =mv
|
on näha, et kiirendus on konstantne siis, kui jõud 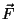 on konstantne.
Kui on konstantne.
Kui 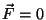 , on kiirendus null ja keha liigub ühtlaselt või seisab
paigal. Aga just seda väidab Newtoni I seadus: kui teiste kehade mõju
puudub või need kompenseeruvad, ongi , on kiirendus null ja keha liigub ühtlaselt või seisab
paigal. Aga just seda väidab Newtoni I seadus: kui teiste kehade mõju
puudub või need kompenseeruvad, ongi
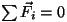
| |
|
Mida hakata peale Newtoni III seadusega? Kui uuritakse ainult ühe
keha liikumist ja teda mõjutavad kehad meid ei huvita, võime nad
vaatluse alt välja jätta. Kui tegu on kehade süsteemiga (aga
igasugune mehhanism on tegelikult kehade süsteem) tuleb seadust
arvestada.
Kui autoga paigalt võttes anname sidurit vabastades gaasi,
rakendame tegelikult Newtoni III seadust: samal ajal, kui siduri üks
ketas pöörab käigukasti kaudu auto rattaid, mõjub teisele kettale
vastassuunaline (mootori pöörlemist pidurdav) jõud. See tuleb
kompenseerida täiendava võimsuse lisamisega (gaasi andmisega),
vastasel juhul sureb mootor välja.
Newton polnud esimene, kes matemaatika abil liikumist uuris. Seda
tegid ka vana-aja mehaanikud Heron, Archimedes jt. Liikumise ja selle
põhjuste üle murdsid pead Leonardo da Vinci, Galileo Galilei,
Evangelista Torricelli, Rene Descartes ja paljud nende kaasaegsed.
Newtoni süsteem ületas kõiki neid varasemaid katseid oma
universaalsusega, võimalike järelduste ja rakenduste tohutu hulgaga.
See, et me teda tänaseni õpime, näitab ainult üht: midagi paremat
pole inimkond viimase 300 aasta jooksul välja mõelnud.
|
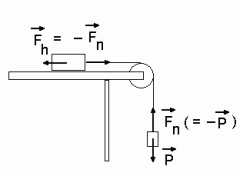
Newtoni III seadus. Hõõrdejõud on tasakaalus niidi pingega, niidi pinge raskusjõuga.
|
|
Miks? Kohe näeme.
Liikumise diferentsiaalvõrrand. Mida
teha aga juhul, kui jõud on muutuv suurus? Esimene mõte: paneme oma
liikumisvõrrandis-polünoomis kiirenduse 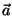 asemele asemele 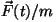 ja
saamegi "muutuva jõuga võrrandi".
Kui see nii lihtne oleks! Juba käesolevas loengus näeme, et kehade
vastasmõju sõltub pigem nende vastastikusest asendist kui ajast. Kui
räägime "muutuvast jõust", ei mõtle me mitte funktsiooni ja
saamegi "muutuva jõuga võrrandi".
Kui see nii lihtne oleks! Juba käesolevas loengus näeme, et kehade
vastasmõju sõltub pigem nende vastastikusest asendist kui ajast. Kui
räägime "muutuvast jõust", ei mõtle me mitte funktsiooni 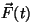 ,
vaid ,
vaid
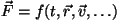 ... Aga liikumisvõrrand nõuab
vaid üht - keha asukoha sõltuvust ajast. ... Aga liikumisvõrrand nõuab
vaid üht - keha asukoha sõltuvust ajast.
|
Liikumisvõrrandi leidmise teeb keeruliseks asjaolu, et uuritavale kehale mõjuv jõud sõltub tavaliselt nii keha asukohast kui kiirusest.
|
Siin tulebki appi diferentsiaalarvutus. Kui võtta ajavahemik
nii lühike, et jõud "samahästi kui ei muutu", võime liikumise lugeda
ühtlaselt muutuvaks. Me võime kasutada Newtoni II seaduse valemit
See on teist järku diferentsiaalvõrrand. Me võime kirjutada ta
koordinaate pidi lahti (tehke seda!), sööta arvutisse (MathCAD
sööb teda hea meelega) ja mõnel lihtsal juhul ka integreerida - viia
kujule, mis rahuldab liikumisvõrrandi üldkuju 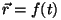 . .
Liikumisvõrrandi lahendeid. Füüsikaülesannetes
sageli esinevad jõudude tüübid on loomulikult ammu läbi rehkendatud.
Toome järgnevalt mõned näited sellest, kuidas käitub liikumise
diferentsiaalvõrrand meile tuttavate jõudude korral. Vaatame, kas
lahendid tulevad tuttavad ette. See, et kasutatakse ühemõõtmelisi
liikumisi, ei tohiks teid enam häirida - oletame, et tegu on näiteks
kolmemõõtmelise vektorvõrrandi ühe komponendi käitumisega. Teised
käituvad samamoodi.
| |
a) Kui jõud on null, on võrrandiks 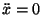 Integreerides
saame: Integreerides
saame:
Siin 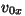 ja ja 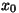 on integreerimiskonstandid; nad võrduvad
kiiruse x-komponendi ning keha x-koordinaadi väärtustega ajahetkel on integreerimiskonstandid; nad võrduvad
kiiruse x-komponendi ning keha x-koordinaadi väärtustega ajahetkel
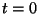 . .
| Jõudude puudumisel või nende summa võrdumisel nulliga liigub keha ühtlaselt (muutumatu kiirusega). |
|
Kui oskate matemaatikat (eksam tehtud?), näidake seda.
| |
b) Kui jõud on konstantne (raskusjõud: 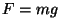 , hõõrdejõud: , hõõrdejõud:
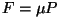 ), on võrrandi lahendiks meie poolt kinemaatika osas
kirjeldatud ning praktikumis proovitud polünoom ), on võrrandi lahendiks meie poolt kinemaatika osas
kirjeldatud ning praktikumis proovitud polünoom
Proovige lahendada difvõrrand konstantse nullist erineva jõu puhul,
kasutades eelmises punktis esitatud võtteid.
|
Konstantse jõu korral keha kiirus kasvab või kahaneb ühtlaselt (muutumatu kiirendusega).
|
c) Kui jõud sõltub ainuüksi ajast, pannakse polünoomi
ruutliikmesse ajast sõltuv kiirendus 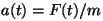 . .
|
Ajast sõltuva jõu korral saame liikumisvõrrandi, kui asendame ühtlaselt muutuva liikumise valemis kiirenduse Newtoni II seadusest. Vt. ülesanded!
|
d) Kui jõud on võrdeline nihkega (näiteks elastsusjõud 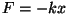 ),
või kiirusega (näiteks takistusjõud ),
või kiirusega (näiteks takistusjõud 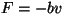 ) tekib väga huvitav võrrand: ) tekib väga huvitav võrrand:
mille üheks lahendiks on sumbuvad võnkumised. Võrrandil on paljudel juhtudel
ilus algebralis-trigonomeetriline lahend, numbriliselt (arvutiga) on
ta kergesti integreeritav. Matemaatikutel on selliste võrrandite kohta
terve teooria.
|
Nihkega võrdeline, kuid vastassuunaline jõud kutsub esile võnkumised.
Kiirusega vastassuunaline jõud peatab liikumise või viib võnkumiste sumbumisele.
|
e) Kui jõud on pöördvõrdeline nihke või selle ruuduga
(näiteks gravitatsioonijõud
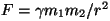 ), tekivad nn.
väljavõrrandid.
Aga sellest juba järgmises loengus. ), tekivad nn.
väljavõrrandid.
Aga sellest juba järgmises loengus.
| |