1. Sissejuhatus
Füüsika nagu iga teinegi õppeaine koosneb kahest komponendist:
teadmised ja oskused. Kui üldfüüsika kursustes piirdub vaid
teadmistega, siis insenerifüüsika juurde kuuluvad paratamatult ka
oskused - võime kasutada füüsikakursuses omandatud teadmisi
tehniliste probleemide lahendamisel. Enamus masinaõpetuse ja
elektrotehnika valemeid ning tehnoloogilisi normatiive on
üle võetud või tuletatud füüsika seadustest; füüsikast on pärit ka
mõõtmistehnoloogia ning statistiline andmetöötlus.
| |
|
Füüsika kui teadus kujutab endast filosoofilist süsteemi, kus
reaalsetele loodusnähtustele seatakse vastavusse nende matemaatilised
mudelid. Igat eset või protsessi püütakse kirjeldada kvantitatiivselt
määratavate parameetrite - füüsikaliste suuruste abil. Nende
parameetrite arvulised väärtused - mõõdud - on omavahel
seotud matemaatiliste seoste - valemitega. See arvude-
valemite kompleks kannab nime matemaatiline mudel.
Matemaatiline modelleerimine võimaldab uurida protsessi
teda reaalselt käivitamata, varieerides mudeli parameetreid ja
jälgides neist sõltuvate suuruste muutumist, st. protsessi käiku.
Mudeli arengut reaalse protsessiga võrreldes saame hinnata mudeli
täpsust ja adekvaatsust (vastavust tegelikkusele) ning teda vajaduse
korral korrigeerida. Kriitilistel juhtudel viiakse läbi katse e.
eksperiment - looduses tavaolukorras mitte esinev protsess, mida on
vaja ühe või teise valemi kontrolliks.
|
Mõõtühikute ning mõõtmisprotsessiga tutvute füüsika laboris. Seal õpitu kuulub loengukursuse juurde, selle omandamist kontrollitakse kontrolltööde käigus.
|
|
Füüsikat õppima asudes oleks hea meeles pidada järgnevaid
põhimõtteid: |
|
| 1. |
Füüsika ei kasuta kvalitatiivseid määratlusi, nagu
ilus, halb, punane, hapu, etc., vaid asendab need
kvantitatiivselt määratavate suurustega nagu pikkus, aeg,
voolutugevus, etc.. Iga suurust iseloomustab tema mõõt -
kujund, mis koosneb mõõtarvust, piirveast ja ühikust. Suuruse ja
mõõtühiku tähistamiseks kasutatakse kokku lepitud
tähtsümboleid, mõõtarv ja viga antakse tavaliselt ümardatud
reaalarvu abil. Ümardamiseks ning vea leidmiseks on seejuures
kindlad reeglid. |
Nähtuste ja esemete kirjeldamiseks kasutatakse füüsikas ainult arve. Valemites ja seadustes olevad tähtsümbolid peavad olema alati asendatavad arvudega.
|
| 2. |
Füüsika seadused kujutavad endast matemaatilisi
seoseid
nimetatud suuruste vahel. Seos püütakse anda valemi
abil,
aga kasutatakse ka graafikuid, tabeleid ja nomogramme. Valem
ongi
matemaatilise mudeli lihtsaim vorm,
| |
| |
AGA | |
| 3. | Iga füüsika
seaduse juurde kuulub ka sõnaline
kirjeldus, mis viitab
põhjuslikule seosele. Matemaatiline
valem on indiferentne, teda
saab matemaatiliselt teisendada,
kusjuures kõik leitud kujud on
samaväärsed. Ka on matemaatiline seos
kehtiv kogu
määramispiirkonna ulatuses, füüsika seadustel on aga
reeglina piiratud rakendusala. Kõik see nõuab sõnalist
selgitust.
|
Füüsika valemite algebralised teisendid ei ole alati
samaväärsed. Kui üks neist kirjeldab põhjuslikku seost
või esineb muid piiranguid, lisatakse sõnaline kirjeldus.
|
| 4. |
Füüsika kursus on
järjepidev, st. tema järgnevad osad
toetuvad eelnevatele.
Nii sisaldab optikakursus elektriõpetuse ja
mehaanika elemente,
kvant-teooria toetub termodünaamikale jne.
|
|
|
Füüsika valemeid võib tinglikult jagada kolme tüüpi:
| |
| 1. | Empiirilised
valemid saadakse mingi katseseeria üldistusena.
Nad on suhteliselt
ebatäpsed (seose kuju sõltub tugevalt
mõõtmistäpsusest) ja ei oma otsest tunnetuslikku
väärtust.
Empiirilise seose tunnuseks on numbriliste parameetrite
rohkus; need
parameetrid on saadud katseseeria matemaatilisel
töötlemisel.
|
|
|
2. | Teoreetilised valemid - põhiseadused - saadakse
empiiriliste valemite üldistamise teel. Nad on matemaatiliselt
keerukad,
mõnd empiirilist parameetrit asendab kindlat väärtust
omavate suuruste, nn. universaalkonstantide kombinatsioon.
| Füüsika
seadused ja neid esitavad valemid jagunevad:
- põhiseadused
- empiirilised sõltuvused
- rakenduslikud seosed
|
| 3. | Rakenduslikud
seosed saadakse eespool toodute
konkretiseerimise tulemusena. Nende
ülesandeks on kindla suuruse
leidmine või jälgimine ette
antud protsessis. On rohkem tehnilise
füüsika ja tehnoloogia
pärusmaa.
|
|
Ülaltoodut arvestades püüan kursuse üles ehitada mitte kui
ajaloolis-filosoofilise ülevaate, vaid peaasjalikult rakenduslikke
vajadusi silmas pidades. Viimaste osas üritan konsensusele jõuda ka
Teie tulevaste eriala-õppejõududega.
Jaak Jaaniste
| |

2. Matemaatiline baas
Et kõik ülaltoodu kehtib ka matemaatikakursuse kohta, siis,
tundes matemaatikute kalduvust teoreetilisuse poole, kordan ma
füüsika õppimisel vaja minevaid matemaatilisi alustõdesid. Ma ei
hakka siin defineerima-tõestama teil juba õpitud asju - võtke
seda kui meeldetuletust. Vajaduse korral võime teha konsultatsioone.
Arvud. Valdavalt on füüsikas suuruste kirjeldajaiks
reaalarvud. Erijuhtudel kasutatakse ka täis-, naturaal- ja
kompleksarve.
Reaalarvude hulk on pidev, st kahe ükskõik kui lähedase
reaalarvu vahele mahub alati veel mõni reaalarv, aga sinna ei anna toppida ühtki mitte-reaalarvu. Muidugi
kuuluvad reaalarvude sekka kõik selle hulga alamhulgad, nagu
ratsionaalarvud, täisarvud jne.
Igapäevaelus ja ka tehnilistes dokumentatsioonides esitatakse
reaalarvud kümnendsüsteemi positsioonarvude kujul. Lahti seletatuna tähendab see, et iga arvu saab kirja panna astmereana, kus
astmealuseks on kümme (10), mille erinevatele astmetele vastavad
kordajad reastatakse astmenäitajate kahanevas järjekorras. Puuduva
astme kordaja tähistatakse nulliga; kohta, kus astendaja muutub
negatiivseks, tähistatakse komaga (lääne õpikutes ja
arvutiprogrammides enamasti punktiga). Kümne astmeid ja liitmismärke
seejuures ei kirjutata.
| |
|
Näiteks:
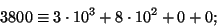
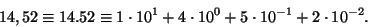
Kui arv on väga suur (väike), st. taga (ees) olevate nullide arv üle
mõistuse, tavatsetakse sobiv kümne aste sulgudest välja tuua. Nii
saadakse ujukoma-arv, näit.
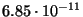 . Mida see
tähendab? Kirjutame lahti: . Mida see
tähendab? Kirjutame lahti:
|
Harjutame:
- positsiooniarvu kirjapanek polünoomina
- püsikoma-arvu teisendamine ujukoma-arvuks ja vastupidi
- aritmeetilised tehted ujukoma-arvudega
NB! Kõik harjutused kuuluvad ka kontrolltöödesse!
|
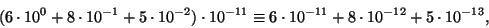
|
|
mis on palju arusaadavam kui püsikoma-arv 0,0000000000685.
Kasuks tuleb, kui teada, et positsiooniarvu saab anda ka 10-st
erineva astme-aluse abil. Arvutiasjandus ja automaatika kasutavad
lisaks kümnendsüsteemile kahend-, kaheksand- ja
kuueteistkümnend-süsteeme.
Täisarvud on loenduv, mittepidev arvusüsteem; kasutatakse indeksitena
mitmekomponendiliste objektide (maatriksid, vektorid, tensorid
etc.) juures ning arvuridade kirjapanekul (summeerimisindeksid).
Täisarve ei saa jagada, sest siis pole tulemuseks enam
täisarv.
Kompleksarvud on algebraline süsteem, mis lubab kirja panna
suvalise astme võrrandi lahendeid. Koosneb reaal-osast (tavaline
reaalarv) ja imaginaar-osast (reaalarvu korrutis imaginaarühikuga
i. Imaginaarühik defineeritakse seosega 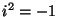 . Matemaatikud
kasutavad kompleksarve II järku diferentsiaalvõrrandite teoorias,
füüsikud ostsilleeruvate (võnkuvate) süsteemide kirjeldamisel, kus
nad annavad tavaliste arvudega võrreldes märksa kompaktsema
esituse. Nii on kvantmehaanika esitatav ainult kompleksarvude
vahendusel, suurt ruumi ja aja kokkuhoidu annavad nad ka
vahelduvvoolu teoorias. . Matemaatikud
kasutavad kompleksarve II järku diferentsiaalvõrrandite teoorias,
füüsikud ostsilleeruvate (võnkuvate) süsteemide kirjeldamisel, kus
nad annavad tavaliste arvudega võrreldes märksa kompaktsema
esituse. Nii on kvantmehaanika esitatav ainult kompleksarvude
vahendusel, suurt ruumi ja aja kokkuhoidu annavad nad ka
vahelduvvoolu teoorias.
Näide kompleksarvu tekkest:
Olgu tarvis lahendada kuupvõrrand 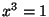 . Tavalahendi . Tavalahendi 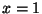 saame
kergesti kätte. Aga astmevõrrandil on lahendeid täpselt nii palju,
kui suur on saame
kergesti kätte. Aga astmevõrrandil on lahendeid täpselt nii palju,
kui suur on 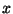 maksimaalne aste. Kuhu kadusid meie
võrrandi kaks ülejäänud lahendit? maksimaalne aste. Kuhu kadusid meie
võrrandi kaks ülejäänud lahendit?
Teeme teistmoodi. Kirjutame võrrandi polünoomina ja jagame tegureiks:
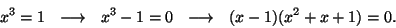
Esimese teguri nullib meie poolt juba leitud lahend 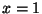 . Teine
tegur annab ruutvõrrandi . Teine
tegur annab ruutvõrrandi 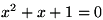 , mille lahendiks on: , mille lahendiks on:
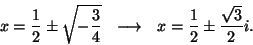
Ongi käes veel kaks lahendit, mis erinevad vaid imaginaarosa märgi
poolest. Selliseid kompleksarvude paare nim. kaaskompleksarvudeks.
Nii palju siis arvudest. Läheme edasi.
| |
|
Algebra.
Matemaatikas nimetatakse algebraks hulka, mis on kinnine kahe
põhitehte ning nende pöördtehete suhtes. Põhiteheteks on liitmine ja
korrutamine, nende pöördteheteks lahutamine ja jagamine. Sõna
"kinnine" tähendab, et näiteks kahe reaalarvu liitmisel saadakse
jälle reaalarv; sama käib ka ülejäänud tehete kohta.
Koolimatemaatikast mäletame algebrat kui tähtsümbolitega arvutamise
kohta käivate reeglite kompleksi. Tõepoolest, kui tähistada reaalarve
väikeste ladina tähtedega, võime kirja panna tunduvalt keerukamaid
matemaatilisi konstruktsioone, kui seda on liitmine või jagamine.
Algebraliste tehete aluseks on võrrand, mis võib esineda
võrduse (näiteks 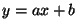 ) või võrratuse ( ) või võrratuse (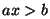 ) kujul. Andes neis
"matemaatilistes lausetes" olevatele sümbolitele arvväärtused
(näiteks ) kujul. Andes neis
"matemaatilistes lausetes" olevatele sümbolitele arvväärtused
(näiteks 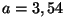 ) saame võrrandist leida teiste arvude (näit. ) saame võrrandist leida teiste arvude (näit. 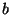 või
või 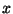 ) väärtuseid. ) väärtuseid.
| |
|
See, et võrduse mõlemal poolel seisavad ühesugused arvud (mis sest,
et erinevate sümbolitega kirja pandud), annab võimaluse võrdust
teisendada, avaldades temast otsitava suuruse. See, et kaks võrdset arvu
jäävad alati võrdseteks ka pärast ükskõik millist matemaatilist
tehet, lubab meil võrduse pooltele liita, lahutada jne. ükskõik
missugust (reaal)arvu. Osava manipuleerimisega saavutame, et
võrdusmärgist vasakule jääb otsitav suurus, paremale kõik ülejäänud.
Ettevaatlik tuleb olla vaid jagamisega: võrduse mõlemaid pooli tohib
jagada vaid sellise tähega, mille väärtus ei saa kunagi nulliks.
Niipea kui tekib nulliga jagamine, kaotab võrdus oma mõtte. Ka
arvutiprogramm peatub sellise takistuse korral.
Võrratusega on pisut keerulisem: negatiivse arvuga
korrutamine/jagamine muudab võrratusmärgi suuna vastupidiseks. Mõelge,
mispärast.
|
Harjutame:
- otsitava suuruse avaldamist algebralisest avaldisest
- võrrandisüsteemi teisendamist lihtvõrrandiks
|
|
Funktsioonid.
Funktsioon on teisendus-eeskiri; ta seab kindla suuruse (argumendi)
väärtusele vastavusse samuti kindla suuruse (funktsiooni). Muidugi ei
tarvitse argumendiks kõlvata ükskõik milline reaalarv, pole ka mingit
garantiid, et argumendi teatud väärtusele ei vasta rohkem kui üks
funktsiooni väärtus.
Loomulikult on funktsioonideks kõik algebralised võrrandid. Kuid
mitte ainult: inimpraktika vajadused on ellu kutsunud terve rea
funktsioone, mis polegi võrrandiga avaldatavad. Koolifüüsikast teame
nn. elementaarfunktsioone, nagu logaritm, siinus, arkustangens
jt. Igaüks neist kirjeldab kindlat matemaatilist seost, aga ükski
neist pole esitatav tavalise, vaid nelja põhitehet sisaldava
avaldise abil.
Elemntaarfunktsioonide leidmiseks on välja mõeldud teravmeelseid
võtteid graafikutest-nomogrammidest kuni ritta-arendusteni. Viimased
on eelistatavad, kuna lubavad funktsiooni väärtust arvutada (koonduva
rea abil) kuitahes täpselt. Et mahukaid arvutusi vältida, koostati
funktsioonide tabeleid (ajalugu tunneb ülimahukaid, 8 - 9
numbrikoha täpsusega logaritmide ning trigonometriliste funktsioonide
tabeleid). Praegu arvutatakse elementaarfunktsioonid kalkulaatori või
personaalarvuti abiga; needki riistad kasutavad ritta-arendusi.
|
|
|
Tuletis ja integraal.
Funktsioonide tabeleid rehkendades märkasid matemaatikud, et paljude
funktsioonide naaberväärtusi saab leida, korrutades argumendi muutu
mingi teise funktsiooni väärtusega samal argumendil. Asja uurinud
W. Leibnitz tuli järeldusele, et funktsiooni muutumise kiirus
argumendi suvalisel väärtusel on kogu määramispiirkonna ulatuses
avaldatav ühe ja sama funktsiooniga, mida ta nimetas tuletiseks
(sks.
Ableitung, ingl.
derivative). Leibnitz'i tähistus
on klassikaline ja väljendab tuletise põhilist ülesannet - ta avaldab
mistahes funktsiooni argumendi mistahes väärtuse jaoks võrdelise
sõltuvuse kujul.
Muidugi kehtib see sõltuvus vaid antud punkti
lähedal, tema nn. "lõpmata väikeses ümbruses", aga - ta loob eelduse
panna kirja diferentsiaalvõrrand, st. seos funktsiooni lõpmata
väikeste muutuste vahel. Et see seos on lineaarne (nii nimetavad
matemaatikud võrdelist sõltuvust), on ka vastav võrrand lihtsama
kujuga.
Juba Newton märkas, et rehkendamine lõpmata väikeste suurustega on
märksa edukam kui füüsikaliste suuruste vahelise seose "ennustamine"
graafiku kuju järgi. Nii saab ringi pindala leidmisel lugeda väikese
sektori pindala võrdseks kolmnurga pindalaga (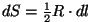 ), vedru lõpmata väikesel venitamisel võime elastsusjõu lugeda
konstantseks ( ), vedru lõpmata väikesel venitamisel võime elastsusjõu lugeda
konstantseks (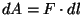 ) jne. Otsitava seose leidmiseks tuleb
nüüd üle minna "normaalsetele" suurustele, liites kokku kõik need
"lõpmata väikesed tükid". Sellisel teel leitud summat nimetataksegi
integraaliks (ld.
integer, tervik). Matemaatikas näidatakse,
et mingist funktsioonist leitud integraali tuletiseks on seesama
funktsioon, seetõttu nimetatakse (määramata) integraali ka
vaadeldava funktsiooni algfunktsiooniks. ) jne. Otsitava seose leidmiseks tuleb
nüüd üle minna "normaalsetele" suurustele, liites kokku kõik need
"lõpmata väikesed tükid". Sellisel teel leitud summat nimetataksegi
integraaliks (ld.
integer, tervik). Matemaatikas näidatakse,
et mingist funktsioonist leitud integraali tuletiseks on seesama
funktsioon, seetõttu nimetatakse (määramata) integraali ka
vaadeldava funktsiooni algfunktsiooniks.
Summa sõltub lisaks liidetavate suurusele ka nende arvust, ja
niisamuti sõltub ka integraal argumendi väärtuste vahemikust, kus
summeerimine-integreerimine aset leiab. Kui antud on
integreerimisvahemiku mõlemad otspunktid, on tegu määratud
integraaliga, millel on ka kindel arvuline väärtus. Kui leitakse lihtsalt
algfunktsioon (määramata integraal), tuleb sellele aga alati liita vabalt
valitava väärtusega konstant. Tuletise väärtust see ei mõjuta, kuna
diferentseerimisel on konstantse liidetava tuletis ("konstandi
muutumise kiirus") null.
|
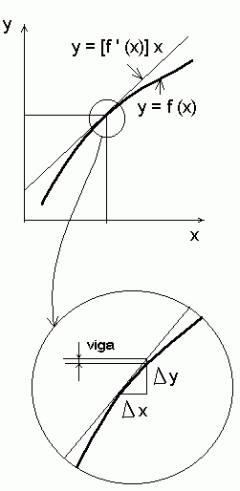
Nii tekib diferentsiaalvõrrand
|
|
Tuletiste ja integraalide leidmist õpetatakse matemaatilise analüüsi
(ingl. calculus) kursuses. Tuletise leidmine on lihtsam, peaaegu
iga valem on esitatav elementaarfunktsioonide kaudu ja nende
tuletised on teada. Vajaduse korral võime kasutada ka liitfunktsiooni
tuletise leidmise algoritmi. Integraalidega on raskem, etteantud
funktsioonidele algfunktsiooni leidmist on alati kasutatud
matemaatilise kirjaoskuse kontrolliks. Praktikas on olud kõvasti
muutunud - suvalise tuletise või integraali saab leida arvuti abiga.
Iseasi, kuidas me saadud tulemust tõlgendada oskame...
Asi, mida iga insener peab aga oskama, on diferentsiaalvõrrandi
koostamine. Põhiprintsiibid on siin üsna lihtsad, aga iga asi tahab
harjutamist. Mida me oma füüsika kursuses kindlasti ka teeme.
|
Harjutame:
- elementaarfunktsioone sisaldava avaldise tuletise leidmine
- liitfunktsiooni tuletis
|
|

Vektorid, tensorid jms.
Matemaatiliste objektide hulk ei piirdu ainult arvudega.
Kõikvõimalike probleemidega tegeledes on inimkond leiutanud
kõikvõimalikke abivahendeid. Nii ka matemaatikas.
Tuleb kohe öelda, et arvutatakse ikkagi ainult arvudega.
Ülal mainitud "matemaatilised objektid" on oma olemuselt arvude
komplektid, mis on kindlal viisil kodeeritud ja mida kasutatakse
kindlal otstarbel. Nii laguneb füüsikaõpetajate lemmik-piinariist
vektor juba tavalises Cartesiuse ristkoordinaadistikus kolmeks
arvuks-komponendiks, liikumisvõrrand kolmeks praktiliselt sõltumatuks
lihtvõrrandiks. Kõik need vektorite liitmised-lahutamised rööpküliku-
jm meetodil on vaid ümberjutustus lihtsatest tehetest tavaliste
arvudega.
Kujutlus vektorist kui noolekujulise otsaga sirglõigust on muide
täiesti täpne. Kui kolmemõõtmelises ruumis on punkti asukoht määratud
kolme lihtarvu - koordinaadiga, siis vektori "pikkuse" ja suuna
andmiseks tuleb tarvitusele võtta veel kolm arvu-koordinaati. Näib,
nagu oleks tegu kuuekomponendilise suurusega... Tegelikult see nii ei
ole, vektor algab alati koordinaatide alguspunktist; ülejäänud
kolm koordinaati näitavad selle keha asukohta, mille juurde antud
vektoriaalne suurus kuulub.
Vektorit kõige üldisemal kujul võimegi kujutada kui üheveerulist
maatriksit, mille ridade arv on võrdne sõltumatute
ruumikoordinaatide arvuga. Millised arvud neis ridades seisavad,
sõltub lisaks vektorile endale meie poolt valitud
koordinaatsüsteemist. Tavaliseks ruumteljestikuks on nn.
ortonormeeritud reeper, mis pannakse kokku kolmest üksteisega risti
olevast ühikvektorist.
Kuidas vektor sellises baasis välja näeb ja kuidas sooritatakse
tehted vektoritega, seda vaatame juba konkreetse füüsika lõigu
juures.
Tensor on vektori üldistus, tema lihtsaimaks analoogiks on
ruutmaatriks. Sellise objekti iga komponendi juures on juba kaks
indeksit, millest üks näitab rida, teine veergu. See on nn. teist
järku tensor (vektorit võiks nimetada esimest järku tensoriks).
Vajaduse korral võime moodustada ka kõrgemat järku tensoreid -
lihtsamaks asi sellest vaevalt et läheb.
Veel tunneb matemaatika spiinoreid, stringe, operaatoreid ja ei tea
kui palju eriotstarbelisi objekte. Meie peame vähemaga toime tulema.
|
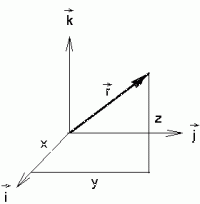
Vektor ja tema kolm koordinaati
|
|
Mitme muutuja funktsioonid ja väljad.
Sõltumatute muutujate arv võrrandis pole millegagi piiratud. Kui need
argumendid muutuvad samaaegselt, on tegu mitme muutuja funktsiooniga.
Seejuures on oluline, et argumentideks olevad muutujad oleks
sõltumatud, st ühtegi neist ei saa avaldada teiste kaudu. Niipea,
kui selline avaldamine on võimalik, muutub mitme muutuja funktsioon
tavaliseks (ühe muutuja) funktsiooniks.
| |
|
Argumentide sõltumatus loob analoogia sõltumatute
ruumikoordinaatidega. Kui vaadelda neid argumente teljevektorite
(ühikvektorite!) kordajatena, saame igale argumentide
kombinatsioonile vastavusse seada kindla punkti ruumis, mille
telgedeks ongi sõltumatud muutujad. Nii on suvaline kolme muutuja
funktsioon esitatav hulgaga, kus igale kolmruumi punktile 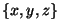 vastab funktsiooni kindel väärtus. Sellist kujundit nim.
väljaks (ingl. field, sks. Feld); väljade uurimiseks on loodud
isegi spetsiaalne matemaatika (või füüsika?) haru - väljateooria.
Väljafunktsiooniks võib olla nii tavaline arv (skalaar) kui vektor
või tensor, vastavalt räägitakse skalaar-, vektor- ja
tensorväljadest.
vastab funktsiooni kindel väärtus. Sellist kujundit nim.
väljaks (ingl. field, sks. Feld); väljade uurimiseks on loodud
isegi spetsiaalne matemaatika (või füüsika?) haru - väljateooria.
Väljafunktsiooniks võib olla nii tavaline arv (skalaar) kui vektor
või tensor, vastavalt räägitakse skalaar-, vektor- ja
tensorväljadest.
|
Matemaatikas on "väli"
mitme muutuja funktsioon,
mida kujutatakse
ruumikoordinaadistikuna.
|
|
Väljafunktsioone saab ka diferentseerida ja integreerida. Veelgi
enam: võimalik on lülitada uuritava ruumi koordinaatide hulka ka funktsioon ise.
Sel juhul määrab iga väljamuutujate vaheline funktsioon selles ruumis
mingi kindlate omadustega alamruumi (näiteks kolmruumi pinna).
Füüsikakursuses tutvume jõuväljadega (on vektorväljad) ja
potentsiaaliväljadega (skalaarväljad) ning õpime rehkendama nende
vahelisi üleminekuid.
| |
|
Programmipakett MathCAD.
Kiirete ning odavate personaalarvutite levik on ellu kutsunud terve
rea matemaatika-alast tarkvara. Algaastate algoritmkeeltest (ALGOL,
FORTRAN, PASCAL, C ja nende arendused) on tänapäevaks jõutud
komplekssete aknareziimis töötavate programmipakettideni, kus
arvutuste teostamiseks on vaja vaid sisestada valem ning defineerida
soovitav arvutus (valemi teisendamine, tuletise või integraali
leidmine, graafiku või tabeli ekraanile kuvamine). See muudab
oluliselt meie suhtumist matemaatikasse: kui varem oli määravaks
arvutuste maht, siis nüüd tuleb peatähelepanu suunata ülesande
püstitusele ja tulemuse interpreteerimisele. Viiekümnendate aastate
"nipitamisele" eelistab tänapäeva matemaatika lihtsaid ja
arusaadavaid, mis sest et töömahukaid algoritme.
Muidugi, olgu arvuti kuitahes võimas, alati on võimalik püstitada
ülesanne, mille lahendamine on "võimaluste piiril" - kas
lahendusaja, vajaliku mälumahu või mõne muu tehnoloogilise piirangu
osas. Ja siis läheb vaja ka nipitamist.
Windows-arvutite meelispakett MathCAD on üks sellistest
universaalsüsteemidest. Tema oskamine on kui mitte hädavajalik, siis
soovitatav. Aga alati tuleb meeles pidada, et ükski arvuti ei asenda
matemaatika-alaseid teadmisi. Ajuvaba lähenemine viib paratamatult
absurdsete resultaatideni, millede paikapanek pole tulemuste tarbija
jaoks tihtipeale võimalik. Mees peab masinast üle olema,
muidu on kraavisõit kindel.
| Kui teil on võimalus õppida MathCAD'i, kasutage seda.
|

