Spikker

Kuidas käsitleda liikumisvõrrandit.

Vektorkujul antud liikumisvõrrandiga on ikka ja jälle probleeme. Et asi ükskord selgeks saaks, annan lühikonspekti. Alguseks lepime kokku tähistes:

1. Mis on liikumisvõrrand?

• on funktsioon, mis määrab liikuva keha (punkti!) asukoha mingil ajahetkel. Võib olla igasugune funktsioon.
• keha (punkti!) asukoha määrab kohavektor, mis antakse kolme koordinaadiga (x,y,z). Need koordinaadid määravad keha asukoha kolmruumi ortonormaalse reeperi suhtes.
• ortonormaalne reeper koosneb kolmest omavahel risti olevast ühikvektorist. Tähistame neid: i, j, k, peale paneme vektorimärgid.

Kokku saame valemi vektorkujul

mis on samaväärne kolme skalaarse võrrandiga:

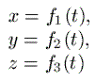Newtoni mehaanikas on kombeks esitada neid võrrandeid ruutpolünoomina

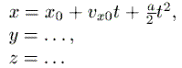Liikumisvõrrandi esimest tuletist nimetatakse kiiruseks:

ja teist tuletist kiirenduseks:

Kui kiirendus on konstantne, on kõik kolm koordinaatvõrrandit samaväärsed koolifüüsikast tuntud "mitteühtlase sirgliikumise" valemitega:

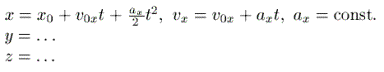See, et me teame,mismoodi liikumisvõrrand välja näeb, ei tee meid targemaks. Me peame oskama teda koostada ja kasutada.

 

2. Liikumisvõrrandi kasutamine.

Olgu meil antud liikumisvõrrand vektorkujul:

Kui see koordinaate pidi lahti kirjutada, saame kolm tavalist võrrandit:

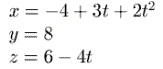Asendades nendesse võrranditesse aja t mingi väärtuse (näiteks t = 3.5 ), saame keha (punkti!) asukoha, st. tema koordinaadid x, y, z sel ajahetkel:

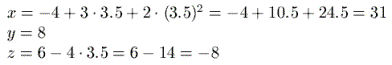Kui küsitakse kiirust, peame võtma kõigist kolmest võrrandist tuletise aja järgi:

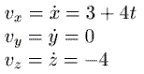ning asendama jällegi aja t väärtused:

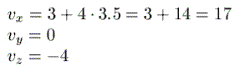Samal moel leitakse kiirendus:

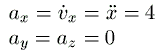Asukoht on asukoht; kiiruse ja kiirenduse kohta võidakse küsida ka suunda. Suunda saab anda nurkadega kiirusvektori ja koordinaat-telgede vahel; kooligeomeetriast teame, et piisab ka kahest nurgast (nurk xy-tasandiga ning nurk vektori projektsiooni ja x-telje vahel tasandil xy).

Kuidas neid nurki leitakse, pidite õppima matemaatika kursuses. Mina piirdun kõige lihtsamaga - küsin nurka vektori ja mingi koordinaattelje vahel. See on nurk kahe vektori (uuritava ja baasivektori) vahel, mille teatavasti määrab skalaarkorrutis:

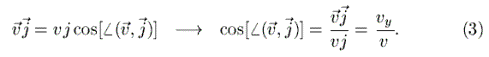Muide - kuna koosinus on paarisfunktsioon (mida see tähendab?), ei määra arkuskoosinus kunagi nurga märki. Ruumilistes ülesannetes pole see tavaliselt oluline. küll aga tasandil. Sel juhul võetakse appi arkustangens ja määratakse, millisele ühikringi veerandile vastab otsitav nurk.

Miks see nii on, tuleb teil mulle eksamil seletada. Seniks aga - kasutage ... 

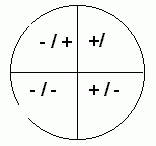
Meie ülesandes on näiteks kiirusvektori nurk x-teljega:

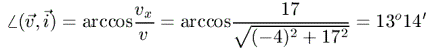Aga  y- ja  z-teljega? Mõelge ja arvutage!

 

Kiirendusega on veel üks vigur. Nagu loengutes kuulsite, jagatakse see kaheks komponendiks:

• normaalkiirendus on kiirenduse komponent, mis on liikumissuunaga risti (suunatud piki trajektoori normaali).

• tangentsiaalkiirendus on kiirenduse komponent, mis on suunatud piki trajektoori puutujat (ingl. tangent - puutuja).

 

Et neid leida, peame kõigepealt leidma nurga kiirus- ja kiirendusvektorite vahel. Loomulikult skalaarkorrutise kaudu

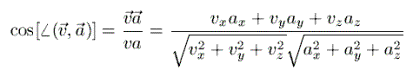Edasi on lihtne: tangentsiaalkiirenduse saamiseks tuleb kiirendusvektori moodul (just moodul, mitte komponendid!) korrutada vektorite vahelise nurga koosinusega, normaalkiirenduse saamiseks aga sama nurga siinusega.

Meie ülesande korral on see lihtne:

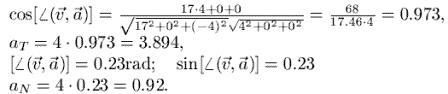Kontrolliks arvutage, kas nende ruutude summa annab välja kiirenduse mooduli ruudu:

Näe - välja tuli!

 

3. Liikumisvõrrandi koostamine

Seda võib mõista kaheti: võrrandit saab "kokku panna", kui on teada kiirendus (pole tähtis, kas konstantne või ajas muutuv) ning keha asukoht ja kiirus vähemalt ühel ajamomendil. Teine - ja hulka tõsisem - on ülesanne, kus liikumisvõrrand tuleb endal tekitada, lähtuvalt konkreetsest ülesandest. Aga see on rohkem teoreetilise mehaanika probleem ja siinkohal me sellega ei tegele.

Niisiis: meil on antud kolm vektorit:

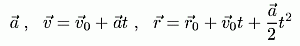ja me otsime liikumisvõrrandit kujul (1). Mis tähendab, et tuleb leida suurused:

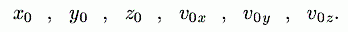
kus indeks "0" tähistab vastava suuruse väärtust hetkel  t = 0 . Kui mõni neist on ülesande algtingimustega antud, võime selle kohe "võrrandisse panna". Kui mitte, tuleb rehkendada.

Teeme näiteks ülesande: Leida liikumisvõrand kui:

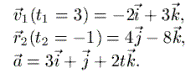Lahendit otsime kujul

mis on "summa kolmest sirgliikumisest. Alustame x(t) leidmisest:

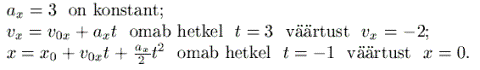Leiame kõigepealt algkiiruse

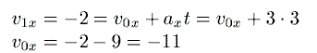seejärel juba algasukoha

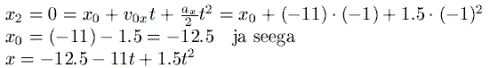NB! See, et lähtevalemeis on mõni baasivektor puudu, tähendab vastava komponendi (koordinaadi, kiiruse, kiirenduse) võrdumist nulliga. Meie ülesandes näiteks x hetkel  t = -1 .

Samal moel leiame y(t).  z-ga on keerulisem: kiirendus pole konstantne, vaid kasvab võrdeliselt ajaga. Seda tuleb arvestada algkiiruse valemis

ning loomulikult ka algasukoha (z-koordinaadi) valemis.

Rehkendage. Vastus peaks olema:

Muuseas - neid valemeid on väga lihtne kontrollida. Pange lõppvastusesse algandmetele vastavad ajamomendid,  rehkendage asukohad ning kiirused ning vaadake, kas algandmed ikka välja tulevad. Kui mitte, hakake viga otsima.

Loomulikult saab neid ülesandeid "edasi arendada". Nii kiirust kui kiirendust saab panna algandmetesse mooduli ja nurkade kaudu; kiirenduse võib anda tangentsiaal- ja normaalkomponendiga. Või pakkuda nurka kiirusvektori suhtes...

Eks proovige. Ja – loodame, et selles tekstis vigu ei ole...

Jaak Jaaniste
veebruar 2004