Loeng 10. Soojusmasinad
18. saj. lõpus, kui arenev tööstus hakkas nõudma suurel hulgal
mehaanilist energiat, leiutati paljudes vee- ja tuuleenergiat
mitte omavates kohtades auru jõul töötavaid seadmeid. Need nn.
atmosfäärimasinad koosnesid tavaliselt silindrist, milles keeva
vee aur tõstis üles raske kolvi. Kolvi jõudmisel
silindri külgseinas oleva avani väljus aur atmosfääri ning kolb
langes alla. Sellised masinad tulid edukalt toime vee
pumpamise või raskuste tõstmisega, kuid ei suutnud anda
tööstusmasinatele vajalikku stabiilse kiirusega pöörlemist. Probleemi
lahendas James Watt 1788. a., leiutades tänaseni kasutusel oleva
aurumasina.
Soojusmasin
=seade, mis muudab soojusenergia
mehaaniliseks tööks.
Masina tööks vajalikku soojust võib saada kütuste põletamisel,
päikese- või tuumaenergiast, vulkaanilistes piirkondades
kasutatakse ka Maa-sisest (geotermaalset) soojust. Mehaaniline
töö tehakse gaaside paisumisel; et aga masin töötaks pidevalt,
tuleb paisunud gaas uuesti algolekusse kokku suruda. Kuidas seda
teha nii, et masin töötaks stabiilselt ja ökonoomselt, on tänaseni
üks tähtsamaid tehnoloogilisi probleeme.
Klassikaline (Newtoni seadustel põhinev) termodünaamika lähtub
kolmest aluspostulaadist, mida nimetatakse termodünaamika
printsiipideks ja nummerdatakse nagu Newtoni seaduseidki - esimesest
kolmandani. Nagu mehaanika liikumisintegraalid, kujutavad ka
termodünaamika printsiibid loodusseadustest tulenevaid
tehnoloogilisi piiranguid. Nende tundmine kuulub seega inseneri
kohustusliku alghariduse juurde.
|
95% tänapäeva energeetikast põhineb soojusmasinatel.
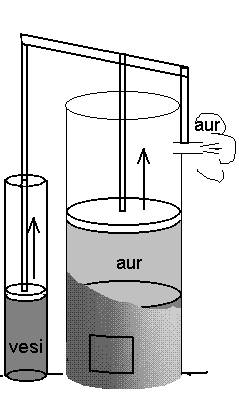
XVIII saj. atmosfäärimasin.
Jämedamas silindris keeb vesi, peenema abil pumbatakse vett kaevanduskäikudest.
|
|
Gaasi töö. Kulgliikumise töö valemid on lihtsalt
kohandatavad gaaside paisumisele. Meie lihtsamas katseseadmes -
silindris liikuva kolvi korral - on
kus
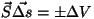 , st. ruumala, mille võrra
suurenes või vähenes kolvi alla jääv ruum. Nagu
jooniselt näeme, on pindala vektor suunatud silindrist väljapoole,
seega vastab ruumala suurenemisele , st. ruumala, mille võrra
suurenes või vähenes kolvi alla jääv ruum. Nagu
jooniselt näeme, on pindala vektor suunatud silindrist väljapoole,
seega vastab ruumala suurenemisele  positiivne,
vähenemisele aga negatiivne väärtus. Tulemus on igati loogiline:
paisumisel gaas teeb tööd, tema kokkusurumiseks peab aga keegi
teine tööd tegema.
Saadud lihtne valem eeldab, et gaasi rõhk jääb kogu paisumise vältel
konstantseks. Kui rõhk muutub, saab ka valem keerulisema kuju - ja
jällegi on see sarnane kulgliikumise töö valemiga: positiivne,
vähenemisele aga negatiivne väärtus. Tulemus on igati loogiline:
paisumisel gaas teeb tööd, tema kokkusurumiseks peab aga keegi
teine tööd tegema.
Saadud lihtne valem eeldab, et gaasi rõhk jääb kogu paisumise vältel
konstantseks. Kui rõhk muutub, saab ka valem keerulisema kuju - ja
jällegi on see sarnane kulgliikumise töö valemiga:
Siiski - kuna rõhk on skaalar, jäävad gaasi paisumise valemid
(väliselt!) mõnevõrra lihtsamateks. Matemaatiliselt on see lihtsus
aga petlik, kuna nüüd on meil tegu mitte joon-, vaid
ruumintegraalidega. Arvuti jaoks on see muidugi ükspuha.
|
Soojusmasinate poolt tehtav töö saadakse gaaside paisumisest.
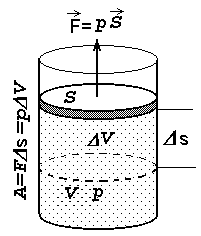
Kolvi liikumisel tehtav töö on võrdeline gaasi rõhuga ning kolvialuse ruumala juurdekasvuga.
|
|
Töö isoprotsessidel. Nagu mehaanikas tahkete kehade
liikumisel, arvutatakse ka gaasi paisumisel tehtav töö integraalina,
süsteemi alg- ja lõppolekust lähtudes. Neid olekuid seob
olekuvõrrand. Kõige lihtsam on rehkendada nn. isoprotsesse, kus
üks parameetritest on konstantne:
1. Isohoorilise protsessi korral on ruumala konstantne, gaas ei
paisu ja järelikult tööd ei tee;
2. Isobaarilisel protsessil, kus rõhk konstantne, kehtib lihtne
valem:
3. Isotermilisel protsessil tuleb avaldada rõhk ruumala ja
temperatuuri kaudu ning lahendada diferentsiaalvõrrand:
|
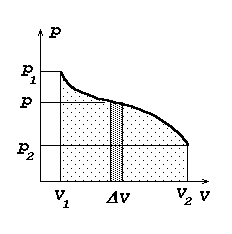
Töö kui integraal:
dA = p dV; kõvera alla jääv pindala saadakse lõpmata väikeste ristkülikute pindalade summana.
|
Avaldame 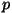 olekuvõrrandist: olekuvõrrandist:
millest pärast integreerimist saame
Küsimus: Kas suudate leida valemi, kus isotermilise
protsessi töö leitakse gaasi alg- ja lõpprõhu kaudu?
Protsesside, mille käigus muutuvad kõik kolm olekuparameetrit, töö
arvutamine on keerulisem. Siin tulevadki appi termodünaamika
printsiibid, mida võib pidada mehaanika liikumisintegraalide
analoogideks.
|
|
|
Termodünaamika I printsiip kujutab endast
energia jäävuse seaduse kirjapanekut:
Gaasile antav soojushulk on võrdne siseenergia
juurdekasvu ning paisumisel tehtava töö summaga.
Täpsustame selle võrrandi liikmete tähendust.
"Soojushulk" on, nagu
ka eelmistes loengutes, gaasile juurde antav energia. Selle
tagajärjel tõuseb gaasi temperatuur, mis molekulaarfüüsika
seisukohalt tähendas tema molekulide kineetilise energia kasvu. Seda
"sisemist" energiat väljendabki võrrandi järgmine liige:
Siseenergia
= keha (gaasi) võime teha tööd sisemiste
(mikro)protsesside arvelt
|
Termodünaamika I printsiip väljendab energia jäävuse seadust gaasi paisumisel.
|
|
Siseenergia liike on palju: kütuste keemiline energia,
tuumaenergia, ergastatud aatomite energia, jms. Kui tegu on ideaalse
gaasiga, samastatakse siseenergia molekulide kineetilise energiaga. Teisi
energialiike sel juhul ei arvestata.
|
Ideaalse gaasi siseenergiaks on tema molekulide kineetiline koguenergia.
|
Täpsustus "töö paisumisel" on samuti oluline: nagu energeetilistes
protsessides ikka, vajab märgiprobleem eelnevat kokkuleppimist.
Antud juhul on nii 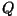 kui kui 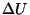 juurdekasvud. Gaasi
paisumine vähendab siseenergiat ja tuleb seega kompenseerida
suurema soojushulga andmisega - seetõttu on juurdekasvud. Gaasi
paisumine vähendab siseenergiat ja tuleb seega kompenseerida
suurema soojushulga andmisega - seetõttu on 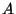 märk positiivne. Ka
kokkusurumisel tehakse tööd, aga kuna see töö suurendab
siseenergiat, peab ta valemis olema negatiivne. märk positiivne. Ka
kokkusurumisel tehakse tööd, aga kuna see töö suurendab
siseenergiat, peab ta valemis olema negatiivne.
|
|
|
Termodünaamiline protsess on üldnimetus kõigi
olekutevaheliste üleminekute kohta. Termodünaamika
I printsiip koos olekuvõrrandiga lubab meil leida valemid
selliste protsesside jaoks, kus ülemineku tee
(vaheolekute pidev jada) on protsessi olemuse poolt ette määratud.
Suhteliselt lihtsad valemid saame isoprotsesside korral:
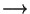 Isohooriline protsess: Isohooriline protsess: 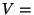 const, const, 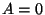 . .
Et
mittepaisuv gaas tööd ei tee, on kogu soojushulk võrdne
siseenergia muutusega:
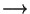 Isobaariline protsess: Isobaariline protsess: 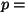 const, const,
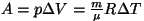
(Mayeri valemist).
I printsiibi võrrand:
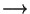 Isotermiline protsess: et Isotermiline protsess: et 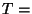 const, siis const, siis
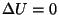 ja ja
Protsessidest, kus muutuvad kõik kolm olekuparameetrit, on
tähtsaim adiabaatiline protsess. See on protsess, mis
toimub soojusvahetuseta (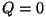 ). Adiabaatilise protsessi korral ). Adiabaatilise protsessi korral
Keerulisem on lugu
olekuvõrrandiga, mis tuleb viia nn. polütroobi kujule.
Polütroobiks (kr polü = mitme + tropos = suund) nimetame
sõltuvust 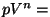 const, kus astendaja const, kus astendaja 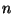 võib omada suvalist väärtust. Nii võiks polütroopseiks lugeda ka
isotermilist (
võib omada suvalist väärtust. Nii võiks polütroopseiks lugeda ka
isotermilist (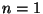 ) ja isegi isobaarilist ( ) ja isegi isobaarilist (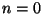 ) protsessi.
Adiabaadi võrrandi leidmiseks asendame rõhu ) protsessi.
Adiabaadi võrrandi leidmiseks asendame rõhu 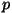 olekuvõrrandist ruumala ja temperatuuri kaudu. Lihtsuse mõttes loeme gaasi hulga võrdseks ühe mooliga ( olekuvõrrandist ruumala ja temperatuuri kaudu. Lihtsuse mõttes loeme gaasi hulga võrdseks ühe mooliga (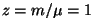 ). Saame: ). Saame:
Ilmselt kujutab see lõigukest adiabaatilist protsessi
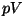 -diagrammil kujutavast kõverast. Kogu kõvera saame,
eraldades muutujad ning integreerides: -diagrammil kujutavast kõverast. Kogu kõvera saame,
eraldades muutujad ning integreerides:
Kui asendada siia olekuvõrrandist 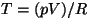 , saame , saame
See ongi adiabaadi võrrand, mida nimetatakse ka Poissoni
võrrandiks.
Astendajat
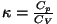 (moolsoojuste
suhe) nimetatakse adiabaadi astendajaks ja teda on lihtne leida
vabadusastmete arvu (moolsoojuste
suhe) nimetatakse adiabaadi astendajaks ja teda on lihtne leida
vabadusastmete arvu 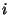 järgi: järgi:
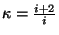 .
Küsimus: Kas oskate näidata, et Poisson'i võrrand kehtib suvalise ainehulga jaoks?
pV- diagramm. Gaasi töö piltlikuks kujutamiseks sobib
kõige paremini graafik, mille telgedeks on rõhk ja ruumala. Et gaasi
töö kujutab nende kahe suuruse korrutist, on sellisel pV-diagrammil
gaasi poolt (või tema kallal) tehtud töö võrdne kõvera ja 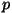 -telje
vahele jääva pindalaga. See, integraalarvutuse õpikutest hästi tuntud
"kõverjooneline trapets" on alati arvutatav, kui on vaid teada rõhu
sõltuvus ruumalast. -telje
vahele jääva pindalaga. See, integraalarvutuse õpikutest hästi tuntud
"kõverjooneline trapets" on alati arvutatav, kui on vaid teada rõhu
sõltuvus ruumalast.
Toome lehe serval ära kõigi loetletud protsesside graafikud
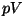 -teljestikus ( -teljestikus (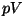 -diagrammid). -diagrammid).
|
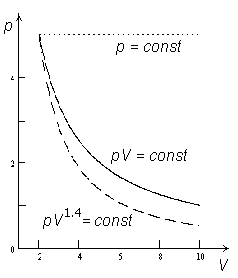
Isobaar (p = const ), isoterm (pV = const ) ja adiabaat (pV1.4 = const) pV-diagrammil
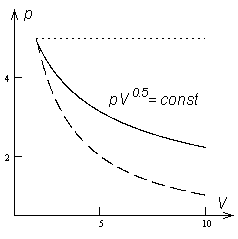
Polütroop indeksiga n = 0.5 pV-diagrammil.
Punktiiriga on antud isobaar (n = 0) ja isoterm (n = 1).
|
|
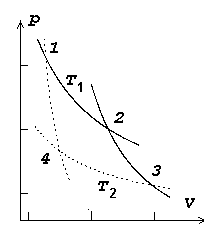
Termodünaamika II printsiip.
Tuleme tagasi soojusmasina probleemi juurde. Võtame ette "tühja"
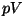 -diagrammi ja paneme sellele kahte "olekut" A ( -diagrammi ja paneme sellele kahte "olekut" A ( ) ning B
( ) ning B
( ) kujutavad punktid. Üleminek ühest olekust teise võib toimuda
erinevaid teid pidi, ja igale teele vastab erinev "töö", st. erineva
kuju ja pindalaga kõverjooneline trapets. ) kujutavad punktid. Üleminek ühest olekust teise võib toimuda
erinevaid teid pidi, ja igale teele vastab erinev "töö", st. erineva
kuju ja pindalaga kõverjooneline trapets.
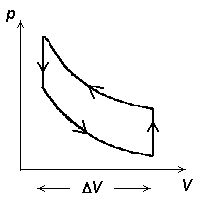
Just siin peitubki soojusmasina ehitamise võimalus. Kui moodustada
diagrammil kinnine kõver nii, et gaasi paisumine toimub piki ülemist
kõverat (suurem töö), kokkusurumine aga piki alumist kõverat (väiksem
töö), kulub kokkusurumiseks vähem energiat kui paisumisel vabaneb.
Selline masin võib toota mehaanilist või elektrienergiat gaasi
siseenergia, st. soojuse arvel.
Ringprotsess
= termodünaamiline protsess, mille
lõppolek langeb ühte algolekuga.
Joonistelt on näha, et kasulik töö tekib ringprotsessil siis,
kui kokkusurumine toimub madalamal rõhul, kui paisumine.
Et väiksem rõhk antud ruumala juures tähendab madalamat
temperatuuri, tuleb töötavat gaasi enne kokkusurumist
jahutada, pärast kokkusurumist aga soojendada.
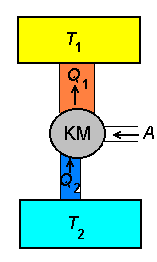
Seega koosneb
soojusmasin kolmest osast:
- soojusallikast, kus kütuse põletamisel tõstetakse gaasi
temperatuuri;
- tööorganist (silindris liikuv kolb), kus gaasi paisumisel tehakse
mehaanilist tööd;
- jahutajast, kus silindris oleva gaasi temperatuuri
alandatakse enne järgnevat kokkusurumist.
On selge, et ka jahutaja poolt ärajuhitav soojushulk  pärineb soojendilt, seega ei muutu kasulikuks tööks mitte kogu
energia:
pärineb soojendilt, seega ei muutu kasulikuks tööks mitte kogu
energia:
Soojusmasina kasutegur
=masina poolt tehtava töö ja
soojendilt saadud energia suhe:
|
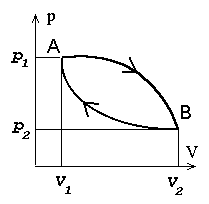
Ringprotsess pV-diagrammil. Üleminekud olekust A olekusse B ja tagasi toimuvad erinevaid teid mööda. Kui protsess kulgeb noolega näidatud suunas, on töö paisumisel (ülemine kõver) suurem kui töö kokkusurumisel (alumine kõver).
Et soojusmasin töötaks (toodaks energiat), tuleb gaasi enne paisumist soojendada, enne kokku surumist aga jahutada.
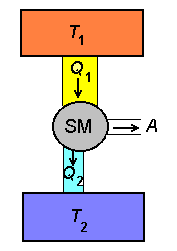
Soojusmasina skeem. Soojusallikalt saadav energiahulk Q1 jaguneb masinas kasulikuks tööks A ning jahutajale antavaks jääksoojuseks Q2.
|
|
Kuna kasutegur oli jõumasinate tähtsaim majanduslik näitaja
(ning osutus äärmiselt väikeseks - esimestel aurumasinatel vaid
paar protsenti), oli möödunud sajandi alguse füüsikutel
kasuteguri probleemiga hulk tegemist.
See uurimistöö lõppes
termodünaamika teise printsiibi formuleerimisega R. Clausiuse
poolt 1850. a.:
Pole võimalik ehitada masinat, mis muudaks temale antud
soojuse täielikult tööks.
Soojus ei voola iseenesest külmemalt kehalt soojemale
Teist liiki perpetum mobile on võimatu
Need on printsiibi sagedamini esinevad sõnastused. Aga vaatame,
kõigepealt ikkagi, millega on tegemist. Tänapäeval kasutatavates
jõumasinates kasutatakse põhiliselt kolme tsüklit:
Aurumasin (J. Watt 1788) - Rankine'i tsükkel:
Tsükli moodustavad kaks isobaari
-katla rõhul toimuv paisumine ja kondensori rõhul (ligikaudu
välisrõhk) toimuv "kokkusurumine", mis tegelikult tähendab
ruumala vähendamist auru välja juhtimise teel. Lõigatud nurk
vastab pärast sisselaskesiibri sulgumist ja enne väljalaskeklapi
avanemist toimuvale adiabaatilisele paisumisele.
Kasutegur sõltub katla rõhust; algul oli see suhteliselt madal
(alla 2 atm., temperatuur 390K); hiljem tõsteti rõhku kuni 10
atmosfäärini. Sellele vaatamata jääb aurumasina kasutegur 10%
piiridesse.
|
Kasutegur näitab, kui suur osa kasutatud soojusest muudetakse mehaaniliseks tööks.
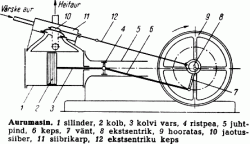
Aurumasin
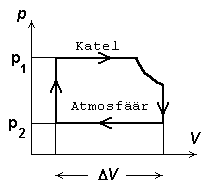
Aurumasina töötsükli pV-diagramm
|
|
Bensiinimootor (C. Benz 1879) - Otto tsükkel
Tsükkel koosneb kahest adiabaadist:
paisumine  ja
kokkusurumine ja
kokkusurumine 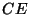 , mille vahel toimub
gaasivahetus , mille vahel toimub
gaasivahetus 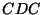 välisrõhul. välisrõhul.
Rõhu (temperatuuri) tõstmine
toimub küttesegu plahvatusega (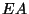 ), rõhu langus ), rõhu langus 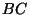 tähendab
gaasi väljalaskmist. tähendab
gaasi väljalaskmist.
Et plahvatuse temperatuur on kõrge
(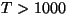 K), on kõrgem ka kasutegur. Piiri paneb kütuse
detonatsioon temperatuuri liig suure tõusu korral kokkusurumise
käigus. K), on kõrgem ka kasutegur. Piiri paneb kütuse
detonatsioon temperatuuri liig suure tõusu korral kokkusurumise
käigus.
|
Bensiinimootori töötsükkel.
|
|
Diiselmootor (R. Diesel 1893) - Diesel'i tsükkel
Sarnaneb põhijoontes Otto tsüklile;
erinevus seisneb plahvatuse asendamisel põlemisega kütuse
sissepritsimisel leekpunktist (kütuse isesüttimistemperatuur)
kõrgema temperatuurini kokkusurutud õhus. Seetõttu toimub
põlemine kõrgemal temperatuuril ning ka kasutegur on kõrgem.
Pealegi kasutab diiselmootor odavamat kütust.
Mootorite analüüs ja võrdlus pole üldfüüsika aine. Kõik toodud
tsüklid sisaldavad kontakti väliskeskkonnaga, mistõttu nende
termodünaamiline arvutus on raskendatud. Soojusmasina
teoreetilise kasuteguri leidmiseks kasutas prantsuse insener
S. Carnot spetsiaalselt konstrueeritud tsüklit.
|
Diiselmootori töötsükkel.
|
|
Teoreetiline kasutegur - Carnot' tsükkel
Oma valemi tuletamisel lähtus
Carnot' asjaolust, et suvalist kinnist tsüklit  -diagrammil
saab esitada lõpmata väikeste, suvaliselt ülesehitatud tsüklite
summana täpselt samuti, nagu tehakse matemaatikas
pindintegraalide arvutamisel. Seega on otstarbekas valida
elementaartsükliks võimalikult lihtsasti arvutatavate
protsessidega piiratud tsükkel. Niisugusteks protsessideks on
adiabaat (ei toimu soojusülekannet) ning isoterm (soojusülekanne
toimub konstantsel temperatuuril.
Kahest isotermist ning kahest
adiabaadist koosnevat ringprotsessi nimetataksegi Carnot'
tsükliks.
Arvutame Carnot' tsüklil töötava
soojusmasina kasuteguri. Selleks peame kogu tsükli vältel
tehtava töö -diagrammil
saab esitada lõpmata väikeste, suvaliselt ülesehitatud tsüklite
summana täpselt samuti, nagu tehakse matemaatikas
pindintegraalide arvutamisel. Seega on otstarbekas valida
elementaartsükliks võimalikult lihtsasti arvutatavate
protsessidega piiratud tsükkel. Niisugusteks protsessideks on
adiabaat (ei toimu soojusülekannet) ning isoterm (soojusülekanne
toimub konstantsel temperatuuril.
Kahest isotermist ning kahest
adiabaadist koosnevat ringprotsessi nimetataksegi Carnot'
tsükliks.
Arvutame Carnot' tsüklil töötava
soojusmasina kasuteguri. Selleks peame kogu tsükli vältel
tehtava töö
jagama gaasile isotermilisel
paisumisel antava soojushulgaga
|
Carnot' tsükkel koosneb kahest isotermist (1 - 2 ja 3 - 4) ning kahest adiabaadist (2 - 3 ja 4 - 1).
|
Töö
isotermilisel kokkusurumisel avaldub samasuguse valemiga
Et adiabaatilisel protsessil soojusvahetust ei toimu, saame
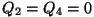 ning ning
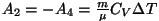 . Kasuteguri valemiks saame
seega . Kasuteguri valemiks saame
seega
Asendades siia
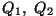 ning taandades ning taandades 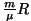 , jääb valem , jääb valem
Seose 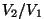 ja ja 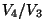 vahel saame adiabaadi võrrandist vahel saame adiabaadi võrrandist
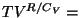 const: const:
Jaganud võrrandid omavahel, taandanud temperatuurid ning
kaotanud astendaja, saame
ja asendades selle
kasuteguri valemisse, saame lõplikult
Näeme, et soojusmasina teoreetiline kasutegur sõltub üksnes
temperatuuridest.
Järelikult pole mingite konstruktsiooniliste
nippidega võimalik antud temperatuuride korral kasutegurit
suurendada.
Kasuteguri parandamiseks on vaid kaks teed: kas
tõsta soojusallika temperatuuri või alandada jahutaja oma.
Tehnikas paneb esimesele piiri materjalide vastupidavus kõrgetel
temperatuuridel, teisele aga töökeskkonna temperatuur.
Kui aga
rääkida teoreetilistest võimalustest, siis on oluline hoopis
teine aspekt: kasutegur on alati väiksem ühest (välja
arvatud juht, kui 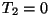 K). Seega K). Seega
|
Carnot' tsükli kasutegur sõltub ainult paisumise ning kokkusurumise temperatuuridest.
|
Pole võimalik ehitada masinat, mis muudaks kogu temale
antava soojuse mehaaniliseks tööks.
See ongi termodünaamika II printsiibi klassikaline
sõnastus.
Võiksime ju vaielda, et kui ikkagi 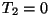 , siis , siis
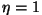 . Paraku pole seegi võimalik - jahutaja mõte seisneb
selles, et me peame talle üle andma mingi soojushulga . Paraku pole seegi võimalik - jahutaja mõte seisneb
selles, et me peame talle üle andma mingi soojushulga
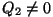 . Niipea, kui me seda teeme, muutub jahutaja
temperatuur nullist erinevaks ning kasutegur väiksemaks ühest.
Pilt on analoogiline perpetum mobile omaga mehaanikas:
mehaanika seadused ei keela igiliikurit, küll aga masinat, mis
teeb tööd eimillegi arvel. (Selle pärast nõutigi keskaegsetelt
leiduritelt, et nende tehtud masin mitte ainult ei liiguks, vaid
teeks ka tööd - näiteks pumpaks vett madalamast anumast
kõrgemasse.)
Analoogia tõttu nimetatakse vahel ka soojust
täielikult tööks muutvat seadet "teist liiki perpetum mobile". . Niipea, kui me seda teeme, muutub jahutaja
temperatuur nullist erinevaks ning kasutegur väiksemaks ühest.
Pilt on analoogiline perpetum mobile omaga mehaanikas:
mehaanika seadused ei keela igiliikurit, küll aga masinat, mis
teeb tööd eimillegi arvel. (Selle pärast nõutigi keskaegsetelt
leiduritelt, et nende tehtud masin mitte ainult ei liiguks, vaid
teeks ka tööd - näiteks pumpaks vett madalamast anumast
kõrgemasse.)
Analoogia tõttu nimetatakse vahel ka soojust
täielikult tööks muutvat seadet "teist liiki perpetum mobile".
|
|
|
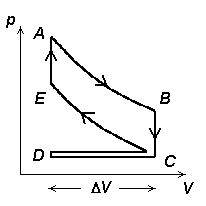
Külmutusmasin ja soojuspump.
Kujutame ette soojusmasinat, mis töötab seniste näidetega
võrreldes pööratud tsükliga, st. kokkusurumine toimub
kõrgemal, paisumine aga madalamal rõhul (temperatuuril).
Valemeist järeldub, et kasulik töö
 , seega
tuleb sellise masina käigus hoidmiseks kulutada mehaanilist
energiat. Teine iseärasus on see, et kuna protsessid kulgevad
vastassuunas, siis tuleb seal, kus varem energiat juurde anti
(soojendati gaasi), seda nüüd ära võtta; seal aga, kus varem
energiat ära viidi (jahutati gaasi), nüüd soojendada. Et , seega
tuleb sellise masina käigus hoidmiseks kulutada mehaanilist
energiat. Teine iseärasus on see, et kuna protsessid kulgevad
vastassuunas, siis tuleb seal, kus varem energiat juurde anti
(soojendati gaasi), seda nüüd ära võtta; seal aga, kus varem
energiat ära viidi (jahutati gaasi), nüüd soojendada. Et
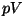 -diagrammil madalamad kõverad tähendavad ka madalamat
temperatuuri, siis pööratud tsükli korral võetakse soojust
külmemalt keskkonnalt ning antakse üle soojemale.
Selline mehhanism kannab külmutusmasina nimetust, kuna ta
võimaldab alandada mingi piirkonna (ruumiosa) temperatuuri.
Tuntuimaks sedalaadi seadmeks on külmutuskapp, kus
sisetemperatuur viiakse välistemperatuurist madalamaks, pumbates
soojust kapi jahutusradiaatorist (madalrõhukamber) väljaspool
kappi olevasse kõrgrõhukambrisse, kus teda enne uut paisumist
jahutatakse.
Ühe dzauli suuruse tööga külmkambrist välja viidavat
soojushulka nimetatakse külmutusteguriks: -diagrammil madalamad kõverad tähendavad ka madalamat
temperatuuri, siis pööratud tsükli korral võetakse soojust
külmemalt keskkonnalt ning antakse üle soojemale.
Selline mehhanism kannab külmutusmasina nimetust, kuna ta
võimaldab alandada mingi piirkonna (ruumiosa) temperatuuri.
Tuntuimaks sedalaadi seadmeks on külmutuskapp, kus
sisetemperatuur viiakse välistemperatuurist madalamaks, pumbates
soojust kapi jahutusradiaatorist (madalrõhukamber) väljaspool
kappi olevasse kõrgrõhukambrisse, kus teda enne uut paisumist
jahutatakse.
Ühe dzauli suuruse tööga külmkambrist välja viidavat
soojushulka nimetatakse külmutusteguriks:
Saadud valem osutab kahele faktile: esiteks on külmutustegur
seda väiksem, mida suurem on temperatuuride vahe ja mida madalam
saavutatav temperatuur. Teiseks, meie igapäevaste temperatuuride
juures on soojuse ümberpumpamine madalama temperatuuriga
keskkonnast soojemasse (õuest tuppa) energeetiliselt kasulikum,
kui sama energiahulga kulutamine vahetult kütmiseks.
Seadeldist, mis töötab külmutusmasina põhimõttel, aga on ette nähtud mitte teatud ruumi jahutamiseks, vaid soojendamiseks madalama temperatuuriga (välis)keskkonna arvel, nimetatakse soojuspumbaks.
Kordajat, mis näitab, kui palju soojust on võimalik ühe dzaulise tööga "tuppa tuua", nimetatakse soojendusteguriks ja tema valem on:
Seega saab
kahekümnekraadise temperatuuride vahe korral ühe dzauliga "üle pumbata" kuni 15 J soojust (temperatuuri 27° C
ehk 300 K juures). Samal ajal tuleb absoluutse nulli lähedastel
temperatuuridel iga üleviidava dzauli kohta kulutada sadu või
tuhandeid dzaule mehaanilist tööd.
Siit veel üks termodünaamika II printsiibi sõnastus:
Temperatuuri 0 K pole võimalik saavutada.
|
Külmutusmasin. Jahutatavast kambrist (temperatuur T2) viiakse soojushulk Q2 üle soojemasse keskkonda (temperatuur T1). Selleks tuleb teha tööd (A).
Külmutusmasina pV-diagramm. Tsükkel kulgeb vastupidises suunas, masin tarbib energiat.
Külmutusmasin võib töötada ka soojuspumbana. Sel juhul loetakse "kasulikuks" mitte jahutajalt võetavat soojushulka Q2, vaid soojendatavasse ruumi viidavat soojushulka Q1.
|
|
Entroopia kasvu seadus - termodünaamika III
printsiip.
Taandatud soojus. Teisendame ideaalse soojusmasina
kasuteguri avaldist:
Suurust 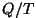 nimetas Clausius taandatud soojuseks ning
formuleeris termodünaamika II printsiibi kui taandatud soojuse
säilivuse ideaalsel protsessil. nimetas Clausius taandatud soojuseks ning
formuleeris termodünaamika II printsiibi kui taandatud soojuse
säilivuse ideaalsel protsessil.
|
Taandatud soojus on seda suurem, mida madalamal temperatuuril toimub soojusülekanne.
|
Tegelikult sõnastas Clausius oma
seaduse pisut teisiti, võrratusena.
Kui vaadelda soojusmasinat
töötava keha (gaasi) seisukohalt, siis on 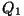 positiivne (keha
sai soojust juurde); positiivne (keha
sai soojust juurde); 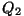 aga negatiivne (soojust anti ära).
Vastavalt on eri märkidega ka taandatud soojused.
Teiseks:
ideaalne masin tähendas seda, et mingeid muid soojuskadusid
peale jahutajale antav soojuse pole - olukord, mida reaalses
masinas pole ilmselt võimalik saavutada. Seega reaalse masina
kasutegur tuleb ideaalse omast väiksem, mis omakorda tähendab,
et temperatuuril aga negatiivne (soojust anti ära).
Vastavalt on eri märkidega ka taandatud soojused.
Teiseks:
ideaalne masin tähendas seda, et mingeid muid soojuskadusid
peale jahutajale antav soojuse pole - olukord, mida reaalses
masinas pole ilmselt võimalik saavutada. Seega reaalse masina
kasutegur tuleb ideaalse omast väiksem, mis omakorda tähendab,
et temperatuuril 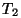 üle kantav soojushulk üle kantav soojushulk 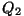 peab olema
suurem, kui ideaalses masinas.
Tulemuseks on taandatud soojuste
ebavõrdsus, mis viib nn. Clausiuse võrratusele: peab olema
suurem, kui ideaalses masinas.
Tulemuseks on taandatud soojuste
ebavõrdsus, mis viib nn. Clausiuse võrratusele:
kus võrdusmärk käib ideaalse, võrratusemärk aga reaalse masina
kohta. Seega "mitteideaalses" ringprotsessis taandatud soojus
väheneb.
|
"Ideaalseks" nimetatakse termodünaamikas protsesse, mis võivad kulgeda mõlemas suunas (protsessid on pööratavad)
|
Et "taandatud soojus" väljendab energeetilist kvaliteeti, peaks
selge olema. Ülekantavast soojushulgast 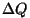 saab seda
rohkem mehaanilist tööd, mida suurem on ülekandel temperatuuride
vahe - st., mida kõrgem on algtemperatuur ja mida madalam
lõpptemperatuur. Et temperatuuri languse määrab äraantud
soojushulk, on järelikult madalamale temperatuurile antav
(suurema taandatud soojusega) soojushulk energeetiliselt
efektiivsem. saab seda
rohkem mehaanilist tööd, mida suurem on ülekandel temperatuuride
vahe - st., mida kõrgem on algtemperatuur ja mida madalam
lõpptemperatuur. Et temperatuuri languse määrab äraantud
soojushulk, on järelikult madalamale temperatuurile antav
(suurema taandatud soojusega) soojushulk energeetiliselt
efektiivsem.
Entroopia. Et soojusülekande kvaliteeti lõpuni mõista,
tuleks veel lahti saada algtemperatuurist. Defineerime suuruse
oletades, et meil on piisavalt hea reservuaar ülekantava
soojushulga mahutamiseks (ilma, et temperatuur muutuks). Suurust
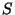 nimetame entroopiaks (kr. entrope -
sees + muundus, eks proovi tõlkida!) ja ta annab veel ühe
võimaluse termodünaamilise süsteemi kirjeldamiseks (on
käsitletav termodünaamilise funktsioonina).
Põhjus, miks just
entroopia on erilise tähelepanu all, on analoogias mehaanikaga:
nagu mehaanilise energia, nii ka entroopia muut ei sõltu
ideaalse pööratava protsessi korral ülemineku tüübist. Seega on
pööratav protsess analoogne konservatiivsete jõududega
mehaanikas; mittepööratavus tähendab soojuse dissipatsiooni
(hajumist), mis väljendub entroopia korvamatus kasvus.
Iga
reaalne protsess, nii mehaanikas kui termodünaamikas,
viib energia kvaliteedi langusele: esimesel juhul läheb
"täielikult kasutuskõlblik" mehaaniline energia üle soojuslikuks
(on kasutatav, st moondatav tagasi mehaaniliseks vaid
osaliselt); teisel juhul väheneb entroopia kasvu tõttu soojuse
kasutatavuse aste (väheneb temperatuuride vahe).
Kui meil on
kinnine tsükkel, mille mingil lõigul on protsess mittepööratav,
saame ühe tsükli jaoks entroopia kasvu nimetame entroopiaks (kr. entrope -
sees + muundus, eks proovi tõlkida!) ja ta annab veel ühe
võimaluse termodünaamilise süsteemi kirjeldamiseks (on
käsitletav termodünaamilise funktsioonina).
Põhjus, miks just
entroopia on erilise tähelepanu all, on analoogias mehaanikaga:
nagu mehaanilise energia, nii ka entroopia muut ei sõltu
ideaalse pööratava protsessi korral ülemineku tüübist. Seega on
pööratav protsess analoogne konservatiivsete jõududega
mehaanikas; mittepööratavus tähendab soojuse dissipatsiooni
(hajumist), mis väljendub entroopia korvamatus kasvus.
Iga
reaalne protsess, nii mehaanikas kui termodünaamikas,
viib energia kvaliteedi langusele: esimesel juhul läheb
"täielikult kasutuskõlblik" mehaaniline energia üle soojuslikuks
(on kasutatav, st moondatav tagasi mehaaniliseks vaid
osaliselt); teisel juhul väheneb entroopia kasvu tõttu soojuse
kasutatavuse aste (väheneb temperatuuride vahe).
Kui meil on
kinnine tsükkel, mille mingil lõigul on protsess mittepööratav,
saame ühe tsükli jaoks entroopia kasvu
|
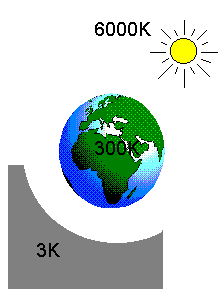
Maapealse heaolu looduslik alus: Maad soojendav Päike (T=6000K) ja jahutajana toimiv maailmaruum (3K). Kasutegur 99.95%.
|
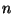 tsükli jaoks tsükli jaoks 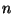 korda rohkem jne. korda rohkem jne.
Nernst'i teoreem. Et hinnata süsteemi koguentroopiat,
tuleb nagu potentsiaaligi korral sisse tuua normeeriv tingimus.
Erinevalt mehaanikas kasutatavatest argumentidest on aga
temperatuuriskaala ühelt poolt piiratud absoluutse nullpunktiga.
See võimaldas W. Nernst'il 1906. a. tõestada teoreemi
mida tihti nimetatakse termodünaamika III printsiibiks.
Tänu Nernsti teoreemile on süsteemi entroopia arvutatav
olekuparameetrite kaudu, mistõttu (erinevalt teistest
termodünaamilistest potentsiaalidest) on ta kasutatav
olekufunktsioonina (võib asendada oleku kirjeldamisel suvalist
olekuparameetrit).
Entroopia arvutamiseks peame oskama avaldada
soojushulka funktsioonina temperatuurist (õigemini selle
funktsiooni tuletist). Näiteks isohoorilise protsessi jaoks
Paistaks nagu lihtne, aga kes julgeb öelda, milline on
isohooriline moolsoojus absoluutse nulli lähedastel
temperatuuridel?
Entroopia kasvu seadus.
Isoleeritud (kinnise) süsteemi entroopia ei kahane.
Kui ei kahane, siis võib ta kas kasvada või jääda konstantseks.
Esimene väide käib suvalise, teine ainult
pööratavate protsesside kohta. Täpselt niisamuti, nagu oli
energiaga kinnises süsteemis: kui jõud olid konservatiivsed, jäi
energia konstantseks, kui mitte, siis energia kahanes.
Ainult et kui energia tähistas töövõimet, siis entroopia
hulk näitab töövõimetust. Et seda häirivat erinevust
kaotada, kasutatakse mõnikord negentroopia mõistet - see
oleks siis sama, mis entroopia, ainult vastasmärgiga.
|
Entroopia väljendab ülekantava soojushulga suhet (jahutaja) temperatuuri. Mida kõrgem on keskkonna tempeatuur, seda raskem on toota kasutuskõlblikku energiat.
|
|
Termodünaamilised potentsiaalid. Kolm olekuparameetrit
moodustavad (matemaatilise) kolmruumi, protsesse kirjeldavad
selles pinnad ja jooned. Tekib kiusatus termodünaamikat
"geometriseerida". Nagu mehaanikas, saab ka siin konstrueerida
potentsiaalivälju, mille kaudu saab lihtsustada protsesside
arvutamist.
Kui entroopia välja jätta, kasutatakse nelja potentsiaali:
- Siseenergia:
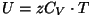 ( (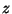 on ainehulk
moolides); on ainehulk
moolides);
- Vabaenergia:
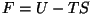 - väljendab "kättesaadavat"
energiat antud temperatuuri ja entroopia juures; - väljendab "kättesaadavat"
energiat antud temperatuuri ja entroopia juures;
- Entalpia:
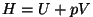 , ka soojusesisaldus -
soojusenergiale lisatakse rõhu potentsiaalne energia; , ka soojusesisaldus -
soojusenergiale lisatakse rõhu potentsiaalne energia;
- Gibbs'i potentsiaal:
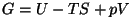 oleks siis
"vabaentalpia", tegelikult võeti käibele võrrandite
sümmeetria kaalutlustest. oleks siis
"vabaentalpia", tegelikult võeti käibele võrrandite
sümmeetria kaalutlustest.
Tänapäeval on termodünaamika suuresti ajalugu; teoreetilistes
uuringutes toetutakse rohkem molekulaarfüüsikale koos
kvantteooria elementidega. Et aga termodünaamika lubab lihtsate
teisenduste abil arvestada ka keemilist energiat, on paljud
siinsed meetodid leidnudki tee keemiasse.
Aga see on juba rohkem, kui üldfüüsikale kohane.
"Tõenäoseim jaotus" ja entroopia. Kujutame
kahest võrdsest poolest koosnevat anumat, milles asub 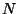 osakest. Tõenäosus, et mingi osake asub näiteks vasakpoolses
ruumiosas, on 1/2. Sarnaste osakeste korral saame tõenäosuse, et
vasakus pooles asub
osakest. Tõenäosus, et mingi osake asub näiteks vasakpoolses
ruumiosas, on 1/2. Sarnaste osakeste korral saame tõenäosuse, et
vasakus pooles asub 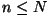 osakest, arvutada binoomjaotuse
abil (nagu "kulli-kirja" probleemi puhul.
Arvutame näiteks
tõenäosused mõnede väikeste osakest, arvutada binoomjaotuse
abil (nagu "kulli-kirja" probleemi puhul.
Arvutame näiteks
tõenäosused mõnede väikeste 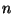 -ide puhul: -ide puhul:
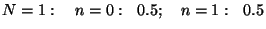
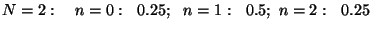
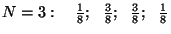
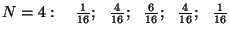
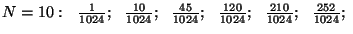
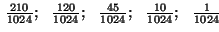
|
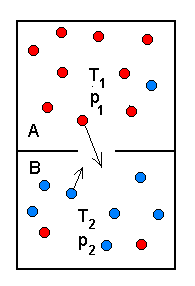
Mittepööratav protsess.
Kui kambreid A ja B ühendav kraan avada, ühtlustuvad kambrites nii rõhud kui temperatuurid. Vastupidise protsessi esile kutsumiseks on vaja väljaspoolt tulevat mõjutust (gaas tuleb tagasi pumbata).
|
Tõenäosus, et mõlemas pooles on ühepalju osakesi, on alati
suurim ja mida rohkem on osakesi, seda väiksemaks jääb
ebavõrdsete jaotuste tõenäosus.
L. Boltzmann seostas selle
entroopia väärtusega, tõestades valemi
kus  on vastava oleku tõenäosus. Seega vastab maksimaalse
entroopiaga olekule alati suurima tõenäosusega olek.
Tulemus on universaalne: ta kehtib nii erinevate gaaside
segunemisel kui ka erineva kiiruste jaotusega
(temperatuuridega) süsteemide ühinemisel. Nimelt selle tõttu
toimub temperatuuride ühtlustumine ja soojuse üleminek kuumemalt
kehalt külmemale. Ka vastupidised protsessid on statistiliselt
võimalikud, kuid molekulide väga suure arvu tõttu ülimalt
väikese tõenäosusega.
Entroopia kasvu seadus tähendab süsteemide üleminekut
maksimaalse tõenäosusega olekusse. Selles seisnebki
termodünaamiliste protsesside pöördumatus. Väidetakse, et
just paljukomponendiliste süsteemide üleminek suurema
statistilise tõenäosusega olekusse määrabki aja kulgemise
suuna - nn. ajanoole. Mida keerukam on süsteem, mida rohkem
see erineb korrapäratust (kaootilisest), seda väiksem
on tema entroopia ning seda vältimatum tema iseeneslik
lagunemine. Keerulised süsteemid ei teki iseenesest (õigemini -
nende iseenesliku tekke tõenäosus on kaduvväike), neid saab
ehitada ainult ümbritseva keskkonna entroopia kasvu arvel.
Maailm tunneb vaid üht süsteemi, kus toimub struktuuri üleminek
lihtsamalt (suure tõenäosusega) olekult keerulisemale (väiksema
tõenäosusega) olekule. See on elusloodus. Termodünaamika
seaduste ilmne rikkumine eluslooduses on tänapäeva teaduse
seisukohalt tingitud informatsiooni kogumisele ja
kasutamisele programmeeritud juhtsüsteemist, mis, töötades
molekulaarsel tasemel, säilitab (arenemisvõimeliste liikide
kujul) just madalama entroopiaga seisundeid. on vastava oleku tõenäosus. Seega vastab maksimaalse
entroopiaga olekule alati suurima tõenäosusega olek.
Tulemus on universaalne: ta kehtib nii erinevate gaaside
segunemisel kui ka erineva kiiruste jaotusega
(temperatuuridega) süsteemide ühinemisel. Nimelt selle tõttu
toimub temperatuuride ühtlustumine ja soojuse üleminek kuumemalt
kehalt külmemale. Ka vastupidised protsessid on statistiliselt
võimalikud, kuid molekulide väga suure arvu tõttu ülimalt
väikese tõenäosusega.
Entroopia kasvu seadus tähendab süsteemide üleminekut
maksimaalse tõenäosusega olekusse. Selles seisnebki
termodünaamiliste protsesside pöördumatus. Väidetakse, et
just paljukomponendiliste süsteemide üleminek suurema
statistilise tõenäosusega olekusse määrabki aja kulgemise
suuna - nn. ajanoole. Mida keerukam on süsteem, mida rohkem
see erineb korrapäratust (kaootilisest), seda väiksem
on tema entroopia ning seda vältimatum tema iseeneslik
lagunemine. Keerulised süsteemid ei teki iseenesest (õigemini -
nende iseenesliku tekke tõenäosus on kaduvväike), neid saab
ehitada ainult ümbritseva keskkonna entroopia kasvu arvel.
Maailm tunneb vaid üht süsteemi, kus toimub struktuuri üleminek
lihtsamalt (suure tõenäosusega) olekult keerulisemale (väiksema
tõenäosusega) olekule. See on elusloodus. Termodünaamika
seaduste ilmne rikkumine eluslooduses on tänapäeva teaduse
seisukohalt tingitud informatsiooni kogumisele ja
kasutamisele programmeeritud juhtsüsteemist, mis, töötades
molekulaarsel tasemel, säilitab (arenemisvõimeliste liikide
kujul) just madalama entroopiaga seisundeid.
|
Entroopia kasv on pidurdamatu protsess.

Monte-Carlo paradoks: mõlemad jaotused on võrd-tõenäosed, kuid omavad kaardimängus väga erinevat väärtust. Kõik õnnemängud tuginevad tõenäosuslikule analüüsile. (Loomulikult mitte mängijate, vaid kasiino omanike huvides.)
|
|
Maxwelli deemon. See on piltlik kujund entroopia kasvu
seaduse rikkumise kohta.
Kujutame, et meie kahekambrilise ruumi
vaheseinas on uks, mida avab ja sulgeb molekulaarsete mõõtmetega
"deemon", avades ukse, kui madalama temperatuuriga ruumist
läheneb kiire (või kõrgema temperatuuriga ruumist
aeglane) molekul. Eeldades, et ukse avamine ei nõua energiat,
saame sel teel tekitada ühes ruumipooles kõrgema temperatuuri
teise ruumi temperatuuri languse arvel - seega vähendada
summaarset entroopiat. Ainus vajalik tingimus sellise "II liiki
perpetum mobile
valmistamiseks on "informatsiooni kasutav
deemon".
Kuidas on lood tegelikult, on lõpuni lahendamata filosoofiline
probleem. Matemaatikud on näiteks seisukohal, et entroopia kasvu
seadus kehtib ka informatsioonivoogude kohta.
Toon näite:
teadmiste mahu plahvatuslik kasv viimase viiekümne aasta vältel
on viinud äärmiselt madalale tõenäosuse, et üks indiviid (või
grupp) suudaks kontrollida saabuva info kvaliteeti. "Deemon",
kes veel sada aastat tagasi oli võimeline eristama tõde valest (infot
mürast), on nüüdseks oma mõju kaotanud ning kaootiliselt liikuv
(väär)informatsioon täidab enamuse inimeste teadvuse.
|
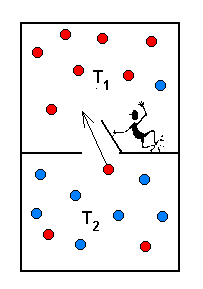
Maxwelli deemon: selektiivne värav kahe ruumiosa vahel võimaldaks panna termodünaamilist protsessi kulgema vastupidises (entroopia kahanemise) suunas.
|
|
On see tsivilisatsiooni lõpp? Vaevalt, sest valik toimib
endiselt. Lihtsamalt öeldes - olelusvõitlus on kandunud
bioloogiliselt tasandilt informatiivsuse tasandile. Kelle
maailmapilt osutub (juhuslikult) sobivaks, elab kriisi üle.
Kellel mitte, see läheb pankrotti. Koos kaaslastega. Möödas on
vaid aeg, kus ühiskondlik teadvus oli juhitav. Õigemini, näis
olevat juhitav.
|
|