Aatomifüüsika
Aatomifüüsika moodustab viimase lõigu traditsioonilises
üldfüüsika kursuses. Selle all mõistetakse kõiki protsesse, mis
toimuvad kehades (aines) mikrotasandil, st. väikseimatest
aineosakestest seespool.
Tegelikkuses kuulub sinna terve
hulk tänapäeva füüsika all-lõike -- lisaks "aatomi ehitust"
käsitlevale veel tuumafüüsika - teadus aatomituuma
ehitusest ja seal toimuvatest protsessidest;
elementaarosakeste füüsika, mis käsitleb tuuma koostisosi;
kvantmehaanika ja kvantväljateooria kui aatomisiseste
protsesside jaoks kujundatud matemaatilist tüüpi abivahendid;
ning lõpuks ka molekulide ja kristallide kujunemist ning kiirgust käsitlev,
sõna-sõnalisest aatomifüüsikast hoopis suuremate objektidega
tegelev füüsika osa, mille jaoks üldnimetus puudub.
Või on see juba keemia all-lõik?
|
Aatomifüüsika käsitleb keemiliste elementide algosakestes - aatomites toimuvaid protsesse.
Aatomifüüsika kitsamas mõttes tegeleb aatomite elektronkatete uurimisega; aatomituumas toimuvaid protsesse uurib tuumafüüsika.
|
|
Aatomite karakteristlik kiirgus.
Nagu kiirguse kvantteooria, sai ka aatomifüüsika alguse
sajandivahetusel. Mõlemad kujunesid ühe ja sama probleemi --
valguskiirguse teke aines -- uurimise käigus. Kiirguse
spektraalne uurimine näitas, et kui pidev soojuskiirguse tüüpi
spekter on omane kondenseeritud ainele (vedelikud ja
tahked kehad), siis gaasides lisandub sellele nn. taust- ehk
foonkiirgusele eraldiseisvatest
sagedustest koosnev joonspekter.
|
Ainete kiirgusspektri kuju sõltub tihedusest: mida hõredam on aine, seda enam kerkib esile joonspekter.
|
|
Joonspektriks nimetatakse viimast aga selle pärast, et
tavalistes piluspektrograafides paistab ta
koosnevat üksikutest heledatest joontest tumedamal taustal.
"Taust" ise kujutab endast joontest tunduvalt nõrgemat (väiksema
intensiivsusega) pidevat spektrit, mille energiajaotus vastab
soojuskiirguse omale. Kõige hämmastavam oli elektriliste
gaaslahenduslampide spekter: madalal rõhul ning temperatuuril
töötavas lambis puudus pidev spekter täielikult; peaaegu kogu
valgus tuli 5 - 10, tihti 1 - 2 kitsa spektrijoonena, mis
andis lampidele iseloomuliku värvuse (neoonlambi punane,
naatriumlambi kollane jne. värvus).
Me teame, et gaase eristab vedelikest-tahkistest molekulide
(aatomite) vahelise vastasmõju puudumine. Siit kohe ka oletus,
et kui pidev spekter on omane kehale tervikuna, siis
joonspekter iseloomustab just kehade koostisse kuuluvate
aatomite kiirgust. Seetõttu nimetataksegi joonspektrit aine
karakteristlikuks kiirguseks.
|
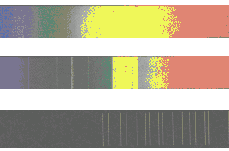
Kolm spektritüüpi: tahke aine, gaas normaalrõhul ja elektriliselt ergastatud hõre gaas. "Vabade aatomite" karakteristlik kiirgus on koondunud kitsastesse joontesse.
|
|
Mida hõredam ja külmem on gaas, seda vähem
kiirgab ta tervikuna ja seda suurem on kontrast atomaarse
kiirgusega. Muidugi peavad aatomid saama kusagilt kiirgamiseks
vajalikku energiat ja kui nad ei saa seda soojusliikumisest,
peab olema teine, näit. elektriline jõuallikas. Aga selleks võib
olla ka valgus või muu elektromagnetkiirgus.
|
Aine karakteristlik kiirgus sõltub ainult aatomisisestest protsessidest.
|
|
Vesinikuaatom
Sageduste näiliselt regulaarne paigutus lausa meelitas otsima
valemeid atomaarse kiirguse sageduste arvutamiseks. Esimese
sellise valemi leidis 1885. a. J. Balmer vesiniku optilise
kiirguse tarbeks.
Et spektrijooned paiknesid geomeetrilist rida
meenutava, lainepikkuse lühenemise suunas tiheneva jadana, sobis
hästi valem
kus 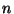 on kahest suurem täisarv
( on kahest suurem täisarv
(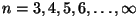 ), ),
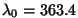 nm aga empiiriline konstant. Valem kirjeldas
ammendavalt kogu vesiniku spektrit, sama tüüpi seoseid õnnestus
leida ka teiste ainete jaoks. nm aga empiiriline konstant. Valem kirjeldas
ammendavalt kogu vesiniku spektrit, sama tüüpi seoseid õnnestus
leida ka teiste ainete jaoks.
Pärast 1900 aastat läks moodi spektraalanalüüs väljaspool
optilist piirkonda. 1906. a. avastas Lyman, et vesinik kiirgab
ka ultravioletis, kusjuures joonte lainepikkused vastavad
valemile
|
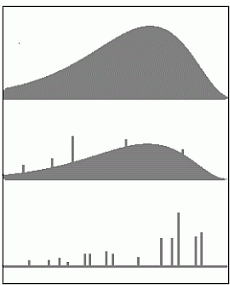
Energiajaotus ülaltoodud spektrites
|
Infrapunases piirkonnas kehtis valem
- see sai avastaja järgi nimeks Pasheni seeria.
Järgnevatel
aastatel lisandus veel kaks infrapunast seeriat (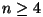 ning 6) ja
küllap oleks rida jätkunud, kui vahepeal teoreetikud suuri
tegusid poleks teinud. ning 6) ja
küllap oleks rida jätkunud, kui vahepeal teoreetikud suuri
tegusid poleks teinud.
|
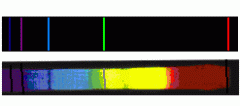
Balmeri seeria vesiniku spektri nähtavas osas.
a) kiirgusspektrina vesinikulambis;
b) neeldumisspektrina kinnistähe Veega (Lüüra alfa) spektris.
|
|
Üldistatud Balmeri valem. Aga esimene asi, mida tegid teoreetikud, oli üldistatud
Balmeri valem. Nimelt märgati, et kui kirjutada Balmeri valem
ümber sageduste jaoks (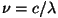 ), saame Balmeri valemi
asemel ), saame Balmeri valemi
asemel
Mis kõige põnevam - sellises formalismis tulid valemite
kordajad 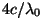 kõigi seeriate jaoks ühesugused.
Nii saadigi füüsika edasist arengut suuresti mõjutanud valem kõigi seeriate jaoks ühesugused.
Nii saadigi füüsika edasist arengut suuresti mõjutanud valem
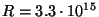 Hz on nn. Rydberg'i konstant. Hz on nn. Rydberg'i konstant.
Spektraalterm. 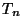 kannab spektraaltermi nime. Niisiis on mistahes seeria
mistahes spektrijoone sagedus määratud kindlate termide vahega.
Sagedust määrav spektraalterm on pöördvõrdeline
täisarvulise konstandi
kannab spektraaltermi nime. Niisiis on mistahes seeria
mistahes spektrijoone sagedus määratud kindlate termide vahega.
Sagedust määrav spektraalterm on pöördvõrdeline
täisarvulise konstandi 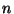 ruuduga.
Valem meenutab varemõpitud
pöördruutsõltuvust; jätame selle meelde edaspidise tarbeks. ruuduga.
Valem meenutab varemõpitud
pöördruutsõltuvust; jätame selle meelde edaspidise tarbeks.
|
Vesiniku spektrijoonte omavahelist paigutust saab kirjeldada täisarvulist argumenti sisaldavate valemite abil.
|
|
Et kogu see matemaatika tehti pärast Plancki valemi 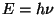 avastamist, võib Balmeri valemit kirjutada ka energia jaoks,
korrutades Rydbergi konstanti Plancki konstandiga
avastamist, võib Balmeri valemit kirjutada ka energia jaoks,
korrutades Rydbergi konstanti Plancki konstandiga 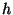 . Et kõiki
neid konstante (lainepikkuse . Et kõiki
neid konstante (lainepikkuse 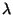 , nurksageduse , nurksageduse 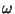 ,
tavalise sageduse ,
tavalise sageduse 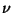 ja energia ja energia 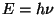 jaoks kehtivaid)
nimetatakse ühteviisi ja tähistatakse samuti ühesuguse jaoks kehtivaid)
nimetatakse ühteviisi ja tähistatakse samuti ühesuguse
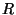 -ga, tekib parasjagu segadust. Ülesannete lahendamisel soovitan
jälgida dimensioone. -ga, tekib parasjagu segadust. Ülesannete lahendamisel soovitan
jälgida dimensioone.
|
|
|
Aatomimudelid.
Valguse ja aine vastasmõju uurimisel rakendasime edukalt nn.
ostsillaatoriteooriat, mille järgi aine koosnes
võnkumisvõimelistest osakestest (atomaarsed ostsillaatorid). Püüdes
sama meetodiga kirjeldada atomaarset kiirgust, jõudis
J. J. Thomson 1903. a. esimese aatomimudelini.
Sõnaga "mudel" tähistavad teadlased mitte harjumuspärast
odavat vähendatud koopiat, vaid originaaliga sarnaselt
funktsioneerivat süsteemi.
Tavaliselt on see nn
matemaatiline mudel - valemite (arvutiprogrammide) kompleks,
mille abil saab kergesti rehkendada välisfaktorite mõju
uuritavasse objekti (süsteemi). Tunnetuse hõlbustamiseks (aga ka
valemite tuletamiseks) tehakse sageli vaheetapina mõtteline
mudel, kus uuritavat süsteemi asendab lihtsam, aga samadel
põhimõtetel töötav objekt.
Aatomi- ja tuumafüüsikas, kus
objektid põhimõtteliselt ei allu vahetule vaatlusele, on
"mudelite uurimine" ainus võimalus mõõtmistulemuste
üldistamiseks.
Seega on kõik aatomimudelid kujuteldavad
makroskoopilised süsteemid, mille (füüsika valemite abil
arvutatud) käitumine on sarnane reaalsete ainete "atomaarsete
suuruste" käitumisele.
|
"Aatomimudel" on kas valemite kompleks (matemaatiline mudel) või sellele vastavalt toimiv makroobjekt, mida kasutatakse teooria(te) illustreerimiseks.
|
|
Thomsoni aatomimudel kujutas endast sfäärilise sümmeetriaga
homogeenset positiivset ruumlaengut, mille väljas liigub
elektron. Elektron oli tol ajal uus asi, tema erilaengu (ning
selle kaudu ka massi) oli Thomson määranud kuus aastat varem
(1897). Ruumlaeng pidi olema võrdne ja vastasmärgiline elektroni
omale, tema ulatuse ("aatomi raadius") rehkendas Thomson
võnkesagedusest.
Tulemuseks oli lihtne seos
kust nähtub, et võnkesagedus on pöördvõrdeline ruutjuurega
aatomi raadiuse kuubist
(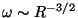 ). ).
|
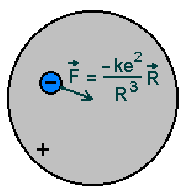
Thomsoni mudel - "rosinapuding".
|
|
Balmeri seeria
joonte sagedustele vastab
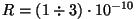 m, mis on
enam-vähem kooskõlas teiste hinnangutega (näit. konstant m, mis on
enam-vähem kooskõlas teiste hinnangutega (näit. konstant 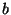 Van der Waalsi
valemis). Van der Waalsi
valemis).
Et vesinik kiirgab väga erinevatel sagedustel, peab olema ka
väga erinevate raadiustega vesinikuaatomeid. Kuna joonspektrid
olid omased kõigile ainetele, tuli välja ülimalt kirju
pilt. Asjasse selguse loomiseks alustati eksperimente ,
milledest edukaimaks osutus Rutherfordi oma.
|
Kas mäletate loengu "Võnkumised" juurde kuuluvat ülesannet läbi Maa puuritud tunneliga?
Thomsoni mudeli sagedusarvutus on (matemaatiliselt) täpselt sama.
|
|
Rutherfordi katse ja planetaarne mudel.
Laengute jaotumise uurimiseks on kõige lihtsam suunata
ainesse laetud osakeste kimp ja jälgida nende trajektoori
muutumist. Osakesed peavad olema küllalt väikesed (muidu ei
kõverdu trajektoor märgatavalt) ja uuritava aine kiht
võimalikult õhuke (et vähendada kahe- ja rohkemakordsete
hajumiste osa). Rutherford kasutas radioaktiivse preparaadi
(raadiumi) poolt kiiratavaid 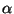 -kiiri ning üliõhukeseks
leheks valtsitud kulda. -kiiri ning üliõhukeseks
leheks valtsitud kulda.
Arvutuste lähteandmeteks olid
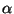 -osakese erilaeng -osakese erilaeng 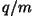 ning kulla tihedus ja
aatommass. ning kulla tihedus ja
aatommass. 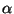 -osakeste kiiruse määras kiirendava elektrvälja
potentsiaal (vaata Lorentzi jõu kohta käivaid ülesandeid
elektromagnetismi osas
( -osakeste kiiruse määras kiirendava elektrvälja
potentsiaal (vaata Lorentzi jõu kohta käivaid ülesandeid
elektromagnetismi osas
(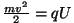 ), nende arvu kindlaks teha tsinksulfiidiga kaetud
ekraanil ilmuvate sähvatuste järgi. ), nende arvu kindlaks teha tsinksulfiidiga kaetud
ekraanil ilmuvate sähvatuste järgi.
Määratavaks seoseks oli
kõrvalekaldunud osakeste suhtelise
arvu sõltuvus kõrvalekaldenurgast.
Katse kirjelduse koos
eeldatava nurkjaotuse valemiga võib leida pea kõigist füüsikaõpikutest
(vt. näit. Saveljev, Füüsika III, lk. 227 - 232).
|
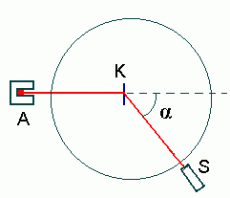
Rutherfordi katse skeem.
A - osakeste allikas;
K - märklaud (kuldleht);
S - stsintsilloskoop (mikroskoop, mille ette on pandud tsinksulfiidiga kaetud ekraan).
Mõõdetakse hajumisnurka 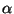 . .
|
|
Hajunud osakeste tegeliku nurkjaotuse täpne vastavus
punktlaengute väljast arvutatule ongi katse põhitulemus.
Seevastu sageli pakutav "aatomituuma läbimõõt" on vaid
positiivse laengu maksimaalne ruumiline ulatus -
energia valemist
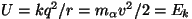 leitud
"ümberpööramisraadius" leitud
"ümberpööramisraadius" 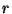 . Kui panna selline . Kui panna selline
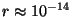 m Thomsoni valemisse, saame võnkesagedused
suurusjärgus m Thomsoni valemisse, saame võnkesagedused
suurusjärgus 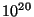 Hz, mida ei saa kuidagi õigeks lugeda. Hz, mida ei saa kuidagi õigeks lugeda.
Niisiis - mudel, kus elektron võngub tuuma sees, pole
võimalik. Järelikult peab ta võnkuma tuuma ümber.
Mehaanika seisukohalt on seegi võimalik. Veelgi enam: uus
ülesanne pole midagi muud, kui masspunkti liikumine
pöördruutsõltuvusega jõuväljas, st. kõige enam uuritud
mehaanikaülesanne.
Lihtne arvutus lähtevalemitega
|
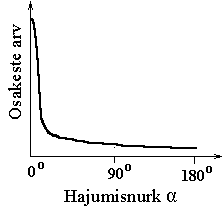
Rutherfordi katse tulemus.
|
annab vesiniku (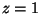 ) Balmeri joone ) Balmeri joone 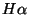 (
(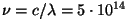 Hz) korral ringorbiidi raadiuse Hz) korral ringorbiidi raadiuse
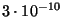 m. m.
Seega sama tulemus, mis Thomsoni mudeli
korral. Pole midagi üllatavat: nii väljatugevus kui võnkesagedus
on ju samad!
Rutherfordi mudeli kiire populaarsuse tegelikuks põhjuseks on
tema sarnasus Päikesesüsteemiga. Keskel on massiivne tuum
(Päike), selle ümber tiirlevad ringikujulistel orbiitidel
elektronid (planeedid). Et astronoomia on populaarne teadus,
sobis selline piltlik mudel hästi inimestes kinnistunud
maailmapildiga. Seda enam, et "tegelikku" aatomit nagunii keegi
kunagi ei näe.
|
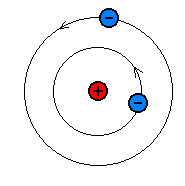
"Planetaarne" aatomimudel.
|
|
Piltidel on siiski oluline erinevus. Planeedid liiguvad
maailmaruumis takistuseta ja seetõttu on Päikesesüsteem
miljardite aastate jooksul püsinud muutumatuna.
Aatomis liikuv
elektron seevastu peab kiirgama elektromagnetlaineid, st.
kaotama energiat. Et orbiit sõltub koguenergiast ("kõrgematel"
orbiitidel on see suurem, "madalamatel" väiksem), tähendab
energia kiirgamine elektroni lähenemist tuumale.
Pöördruutsõltuvus 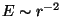 nõuab suurema tõmbejõu
tasakaalustamiseks suuremat orbitaalkiirust ( nõuab suurema tõmbejõu
tasakaalustamiseks suuremat orbitaalkiirust (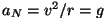 ),
seetõttu väheneb tiirlemisperiood ja koos sellega kasvab
kiiratava valguse sagedus. ),
seetõttu väheneb tiirlemisperiood ja koos sellega kasvab
kiiratava valguse sagedus.
Tulemuseks on kahekordne vastuolu
eksperimendiga: kõigepealt pole "planetaarne" aatom stabiilne,
teiseks ei kiirga ta konstantsel sagedusel.
|
Planetaarse aatomimudeli suurim viga on see, et ta on õige üksnes mittekiirgava aatomi korral.
|
|
Bohr'i teooria. XX sajandi alguse füüsikal oli juba
kogemus selliste olukordade lahendamiseks. Kui miski
klassikalises füüsikas ei klapi, tuleb lihtsalt öelda välja
mingi oletus (hüpotees, postulaat), mis paneb asja klappima.
Esimesena kasutas seda Planck, hiljem Einstein (valguse kiiruse
konstantsuse nõue).
Seetõttu pole ime, et 1913. a. Taani füüsik
Niels Bohr muutis vastuolu seaduseks, sõnastades selle oma
esimeses postulaadis:
Elektronid võivad aatomis
liikuda ainult kindlatel statsionaarsetel orbiitidel. Sellisel
orbiidil liikudes elektron ei kiirga.
Niisiis, statsionaarsel orbiidil elektron energiat ei kaota ja
võib seal püsida igavesti. Edasi on lihtne: selleks, et aatom
kiirgaks, peab elektron orbiiti vahetama.
Elektroni üleminekul suurema
energiaga orbiidilt väiksema energiaga orbiidile aatom kiirgab
kvandi, üleminekul väiksema energiaga orbiidilt suurema
energiaga orbiidile aga neelab selle.
|
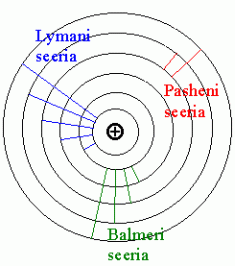
Koolifüüsika tavajoonis: planetaarne mudel Bohr'i orbiitidega.
|
|
Järelikult pole kiirguse lainepikkus (sagedus) pole määratud mitte
elektroni tiirlemissagedusega, vaid statsionaarsetele
orbiitidele vastavate energiate vahega. See on täiesti uus
lähenemine - lähtumine mitte aatomi ehitusest, vaid
kiirguse olemusest. Kuna kiirgus koosneb kvantidest, ei saa
aatom kaotada energiat pidevalt, vaid ainult terve kvant
korraga.
Väljend "elektroni üleminek ühelt püsiorbiidilt teisele" on
selle fakti piltlik esitus planetaarmudeli keeles;
samahästi võiks meil olla mingi teine võrdlusobjekt
(ostsillaator, väriseja või keskaegne "tuleaine" flogiston),
mille energia "koosneb kvantidest" (kvandikott?). Ajalooliselt
oleme aga kinni planetaarmudelis ja ega see väga halb mudel
polegi.
Bohri kvantmudeli aluseks on spektraaltermid - kui algselt oli
Rydbergi valemis 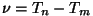 sagedused, siis "Bohri variandis"
on selleks energiad: sagedused, siis "Bohri variandis"
on selleks energiad:
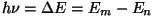 . .
Kui
kirjeldada "energiaterme" planetaarmudeli keeles "ümber tuuma
tiirleva elektroni koguenergiaga 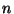 -ndal püsiorbiidil", saame -ndal püsiorbiidil", saame
|
Bohr'i postulaatid pole midagi muud, kui Rydberg'i spektraaltermid, kirja panduna planetaarmudeli näitel ning kiirguse kvant-teooria keeles.
Lugege lõik veel kord läbi. Kas saite aru?
|
lisades siia veel "jõudude tasakaalu"
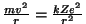 , võime leida ka "orbiidi raadiuse" , võime leida ka "orbiidi raadiuse"
ning "orbiidi pikkuse" (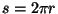 ) ja "elektroni kiiruse orbiidil". ) ja "elektroni kiiruse orbiidil".
Ühtki
neist suurustest pole kunagi mõõdetud, ka pole nad määratavad
kaudsel teel - nad on kõigest "planetaarmudeli parameetrid".
|
|
|
Naatriumi spekter. Füüsikaõpikute üldlevinud
kontseptsiooni järgides peaksin nüüd seletama, kuidas Bohri teooria
rakendamine teistele aatomitele (heelium, liitium jne)
ebaõnnestus ja kordama lauset Bohri kvantteooria
ebajärjekindlusest. Et ma sellest ise hästi aru ei saa, võtan vahele
ühe pooleldi unustatud teooria. See on Rydbergi valem naatriumi
spektrijoonte kohta, pärit 1897. aastast.
Rydberg, "üldistatud Balmeri valemi" autor, avastas nimelt
analoogilise seaduspärasuse naatriumiaurude spektris. Naatrium
ise oli sajandivahetuse spektraalanalüüsis levinuim
lainepikkuste etalon, kuna tema tugev kollane joon asus täpselt
optilise spektri keskel. Lisaks sellele on naatriumi spektris
terve rida nõrgemaid jooni, mille Rydberg jagas kolmeks
Balmeri-tüüpi seeriaks: terav, pea-, ja difuusne seeria. Kõigi
seeriate jaoks kehtis "parandatud" Balmeri valem
|
Balmeri tüüpi valemitega saab kirjeldada ka leelismetallide spektreid.
|
Nagu Balmeri valemis, on ka siin 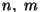 täisarvud, kusjuures täisarvud, kusjuures 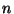 algväärtus oli naatriumil 3,
algväärtus oli naatriumil 3, 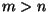 , , 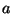 ja ja 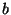 on
mittetäisarvulised parandid. Seeriate nimed vastavad sellele,
millisena Rydberg neid jooni spektrograafis nägi: terava seeria
jooned on nõrgad, kuid kontrastsed, peaseeria omad kõige
tugevamad, difuussel nõrgad ja laialivalguvad. on
mittetäisarvulised parandid. Seeriate nimed vastavad sellele,
millisena Rydberg neid jooni spektrograafis nägi: terava seeria
jooned on nõrgad, kuid kontrastsed, peaseeria omad kõige
tugevamad, difuussel nõrgad ja laialivalguvad.
Hiljem, katseandmete kogunedes, selgus, et see valem kehtib
kõigi leelismetallide jaoks. Muidugi tulevad parandusliikmed
erinevad, kuid meie jaoks on oluline, et ka siin
sõltuvad energiatasemed täisarvude ruutudest.
Lainemehaanika
"Kvanditud energiatasemete" e. statsionaarsete orbiitide
olemasolu aatomis viib mõttele, et igasugune liikumise muutus
peab olema diskreetne (hüppeline), kuna muidu kanduks energia
üle pidevalt. Et jõuväljad, kus liikumine toimub, on
pidevad
(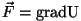 on pidev funktsioon), jääb üle vaid
võimalus, et hüppeliselt toimub tee valik. on pidev funktsioon), jääb üle vaid
võimalus, et hüppeliselt toimub tee valik.
Niisugust asja
kogesime me mäletatavasti optikas interferentsinähtust
kirjeldades -- valguskiir suundub pärast pilu(de) läbimist
sinna, kus keralainete liitumisel on võnkeamplituud maksimaalne.
Kui rääkida kvantfüüsika keeles, siis määrab valguskiire
trajektoori tingimus
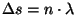 , mis on väga sarnane
Plancki tingimusele , mis on väga sarnane
Plancki tingimusele
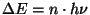 . .
|
|
|
Lainehüpotees. 1923. a. avaldas Louis de Broglie
ajakirja Comptes Rendus (lad. Aruanne, mõeldakse Prantsuse
Akadeemia jooksvat aruannet, oli 19. saj. mandri-Euroopa
tähtsaim teadusajakiri) oktoobrinumbris artikli "Fermat'
printsiip mehaanikas", kus tuli välja järgmise väitega:
Mehaanika vähima mõju
printsiip on ekvivalentne Fermat' printsiibiga optikas, kui
keha impulss
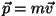 asendada lainearvuga valemi asendada lainearvuga valemi
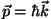 abil.
Teiste sõnadega: omistades liikuvale osakesele lainepikkuse abil.
Teiste sõnadega: omistades liikuvale osakesele lainepikkuse
võime trajektoori leidmisel kasutada interferentsivalemeid.
|
Kvant- ehk lainemehaanika rajaja L.deBroglie hakkas kasutama mittepidevate funktsioonide illustreerimiseks interferentsivalemeid.
|
|
Seega arvutuslikku tüüpi lihtsustus. Kui rakendada seda kinnisel
orbiidil liikuvale elektronile, saame "seisva laine tingimuse"
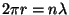 . Ainult sellise orbiidi korral on osake
"nullist erinev", ülejäänud juhtudel temale vastav laine
kustutab iseenda interferentsi käigus. . Ainult sellise orbiidi korral on osake
"nullist erinev", ülejäänud juhtudel temale vastav laine
kustutab iseenda interferentsi käigus.
Et asjasse selgust tuua, arvutame Bohri valemitest elektroni
impulsi ja võrdleme sellele vastavat lainepikkust orbiidi
pikkusega 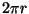 . .
Lähtume valemeist
Lähtudes impulsist 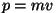 saame lainepikkuseks saame lainepikkuseks
Orbiidi pikkus on
Niisiis vastab esimesele Bohri orbiidile üks, teisele kaks, jne
lainepikkust. Lainepikkus ise kasvab vastavalt impulsi, seega
elektroni orbitaalkiiruse vähenemisele. Et energia on võrdeline
sagedusega (pöördvõrdeline lainepikkusega), väheneb samal ajal
"energianivoode vaheline kaugus". Kõik täpselt nii, nagu vaja.
Muide: ka Max Planck pidas oma "energiakvante" arvutuslikku tüüpi
abivahendiks. Alles Einstein hakkas rääkima "footonitest".
Igasuguse teooria mõte seisnebki selles, et lihtsustada arvutusi või midagi
ennustada. "Laine" sissetoomine küll midagi lihtsamaks ei
muutnud ja küllap oleks ta unustatud, kui mitte E. Schrödinger
1926. aastal poleks leidnud võrrandit, mille abil sai lainet
(täpsemalt nn. lainefunktsiooni) arvutada teoreetilise
mehaanika sümboolikast lähtudes. Seejuures jääb lainefunktsioon
ise tavaliselt leidmata (mitte et ei osata, vaid et kedagi ei
huvita!), piirdutakse vaid süsteemi (aatomi, molekuli) nende
energiate, mille korral lahend eksisteerib, leidmisega.
Kuna kiiratava kvandi sagedus sõltub üksnes energiast, annab
"lubatud energiate" teadmine võimaluse spektrit ennustada.
Aga just see oligi füüsikute eesmärk. Ennustada sagedusi
(spektrijooni), mitte aga rehkendada "elektroni liikumist aatomituuma
ümber".
|
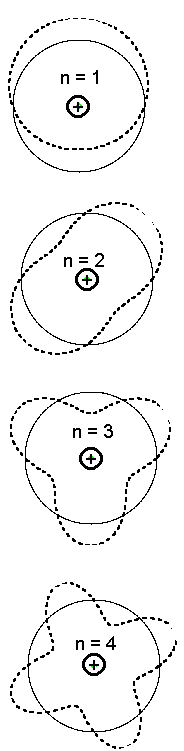
Bohr'i aatomimudeli statsionaarsed orbiidid, joonistatuna seisevlainete kujul.
|
|
Elektronide difraktsioon ja Davisson-Germer'i katse.
Kui õpikutes räägitakse elektronide difraktsioonist, siis
illustreeritakse seda tavaliselt optikakursusest tuntud Young'i
katse analoogiga:
Paralleelsetele piludele (või aukude paarile) langeb elektronide
juga. Et de Broglie järgi vastab see tasalainele, tekib pilude
taha pandud ekraanil interferentspilt - tumedate ja heledate
ribade vaheldumine. Kui sulgeda üks piludest või kiiritada neid
kordamööda, tumedaid ribasid ei teki, jääb vaid tavaline
hajumine.
Õige ta on, aga ärge võtke seda tõestusena. Niisugust katset
pole keegi kunagi teinud ega saagi tegema. Juba nähtava valguse
korral on Young'i katse eksperimenditehnika piiril, koolilaboris
pole teda tavaliselt võimalik läbi viia (kasutatakse kaksikpeeglit
või kaksikprismat). Elektroni "lainepikkus" on nähtava valguse omast
tuhat korda väiksem (kiirusel 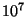 m/s, mis vastab
elektronkiiretorudes tavalisele pingele 1000 V, on lainepikkus m/s, mis vastab
elektronkiiretorudes tavalisele pingele 1000 V, on lainepikkus
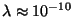 meetrit e. 0.1 nm) - sellise
"laiusega" pilu pole võimalik teha juba aine atomaarse ehituse
pärast. Niisiis on tegu mitte eksperimendi, vaid
illustratsiooniga. meetrit e. 0.1 nm) - sellise
"laiusega" pilu pole võimalik teha juba aine atomaarse ehituse
pärast. Niisiis on tegu mitte eksperimendi, vaid
illustratsiooniga.
Katse, mis kinnitas (vähemalt arvab nii valdav enemik füüsikuid)
elektronkiire laineiseloomu, tehti tolsamal 1924. aastal
C. J. Davissoni ja L. H. Germeri poolt nende
röntgenstruktuuranalüüsi laboris (muide, selliste asjadega
tegeldi ka instituudis, kus töötas de Broglie!). Elektronkiir
suunati kristallpreparaadile, mida eelnevalt oli vaadeldud
röntgenikiirtes; elektrone kiirendav pinge valiti aga selline,
et nende lainepikkus oleks võrdne varem kasutatud röntgenikiirte
omaga. Piltide identsus pluss selle muutumine pinge muutmisel
kinnitas lainehüpoteesi ja de Broglie valemi õigsust.
Lainemehaanika klassikalise demonstratsioonikatse mõtles välja
esimese aatomimudeli autori J.J.Thhomsoni poeg George Paget Thomson.
See on Rutherfordi katse analoog, kus 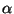 -osakeste asemel
kasutatakse elektrone.
Pärast metall-lehe läbimist hajub elektronkiir, aga mitte
ühtlaselt, nagu Rutherfordil, vaid rõngastena, nagu hajuvad
valguskiired väikeselt avalt. Lihtne katse, aga keeruline
teooria. Klassikalise füüsikaga pole siin midagi teha. -osakeste asemel
kasutatakse elektrone.
Pärast metall-lehe läbimist hajub elektronkiir, aga mitte
ühtlaselt, nagu Rutherfordil, vaid rõngastena, nagu hajuvad
valguskiired väikeselt avalt. Lihtne katse, aga keeruline
teooria. Klassikalise füüsikaga pole siin midagi teha.
|
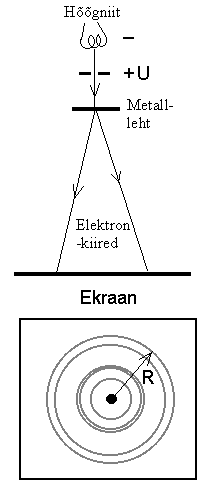
G.P.Thomsoni katse
Kiirendava pinge U muutmisel muutuvad difraktsioonirüngaste läbimõõdud.
Küsimus: Kas suuremale pingele vastavad suuremad või väiksemad rõngad? Vihje: mõelge lainepikkusele!
|
|
Proovime korraks piltlikult ette kujutada seda õnnetut elektroni,
mis füüsiku tahtel läbi ava, pilu või metall-lehe lendab.
Me tunnustame Rutherfordi-Bohri-de Broglie aatomimudelit.
Niisiis ei kohta elektron mingeid "pilu servi", mida me
tavaliselt paberile joonistame. Tema ees on peaaegu kosmiline
tühjus, kus jõudude tasakaalul põhineva korrapära järgi
paiknevad aatomituumad - kaduvväikeste mõõtmetega laengud,
elektrostaatilise välja allikad. Nende ümber tiirlev-võnkuv
"elektronpilv" moonutab seda jõuvälja, pealegi asub kusagil ka
elektron ise, samuti ülitugeva välja allikas.
|
|
|
Kuidas meie elektron selles väljade müriaadis oma tee leiab, ei
saa me kunagi teada. Samuti ei tea me, mida ta tegelikult
kujutab. Nagu ütles üks marksismi klassikutest, on see probleem
ammendamatu. Aga me oskame rehkendada elektronide kogumi
- elektronkiire käitumist; ja seda tehes konstrueerida
elektronlampe, kineskoope, elektronmikroskoope jms.
Arvutamisel kasutame lainemehaanikat kui mugavat ning
enam-vähem mõistetavale "klassikalisele" analoogile tuginevat
algoritmi.
Lainefunktsioon ja Schrödingeri võrrand. Leppinud
sellega, et elektron on laine, paneme kirja lainevõrrandi:
|
"Laineteooria" pole elektroni kui objekti kirjeldus, vaid klassikalisel füüsikal põhinev arvutusalgoritmi illustratsioon.
Schrödingeri võrrandi tuletuskäik on illustratiivne ega kuulu kohustusliku materjali hulka.
Aga ta on Teie matemaatilise lugemisoskuse proovikivi.
|
|
Lainevõrrand
|
|
Selline nägi välja ruumis leviva tasalaine võrrand.
Mäletatavasti oli ta lahendiks teist järku
diferentsiaalvõrrandile
|
|
|
Laine diferentsiaalvõrrand
|
Meile selline võrrand midagi ei anna, kuna tema lahend on juba
kirjas.
Proovime leida "oma võrrandit" mehaanikast tuntud
seosest
|
|
|
Energia avaldatakse impulsi kaudu
|
mis oleks laine kiirust
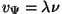 "asendav" seos. "asendav" seos.
Kirjutame kõigepealt lainevõrrandi "kvantmehaaniliseks".
Asendame
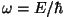 (Planck'i valemist (Planck'i valemist 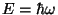 ,
lainevektori ,
lainevektori
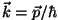 (de Broglie valemist (de Broglie valemist
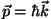 )
ning läheme üle eksponentkujule: )
ning läheme üle eksponentkujule:
|
|
|
"Kvant-teoreetiline" lainevõrrand eksponentkujul
|
Kujutame (lihtsuse mõttes), et laine levib 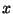 -telje suunas.
Sel juhul -telje suunas.
Sel juhul
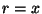 , ,
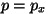 , ,
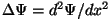 . .
Et saada
laine 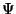 diferentsiaalvõrrandit, mis rahuldab seost (*),
tuleb avaldada osakese energia diferentsiaalvõrrandit, mis rahuldab seost (*),
tuleb avaldada osakese energia 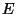 ja impulss ja impulss 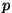 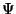 tuletiste kaudu.
tuletiste kaudu.
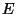 saame, diferentseerides lainevõrrandit saame, diferentseerides lainevõrrandit 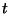 järgi:
järgi:
|
|
millest
|
Energia avaldatakse lainevõrrandi ajalise tuletisena
|
Viimane teisendus tähendab lugeja ja nimetaja 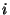 -ga
korrutamist: -ga
korrutamist: 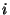 tuleb lugejasse, nimetajasse jääb tuleb lugejasse, nimetajasse jääb 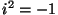 . .
Analoogiliselt leiame 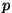 , võttes teise tuletise , võttes teise tuletise 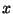 järgi: järgi:
|
|
millest
|
Impulsi ruut avaldatakse lainevõrrandi ruumtuletisena
|
Jääb veel saadud võrrand 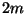 -ga läbi jagada ning eelmisega
võrduma panna: -ga läbi jagada ning eelmisega
võrduma panna:
Kui 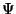 nimetajast ära kaotada (st. võrduse mõlemat poolt nimetajast ära kaotada (st. võrduse mõlemat poolt
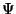 -ga korrutada), on meil käes Schrödingeri
võrrand vaba osakese jaoks. -ga korrutada), on meil käes Schrödingeri
võrrand vaba osakese jaoks.
|
Leitud suurused pannakse Newtoni mehaanika kineetilise energia avaldisse - saadakse vaba osakese võrrand.
|
|
Kui osake liigub konservatiivses jõuväljas, tuleb kineetilisele
energiale 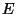 lisada potentsiaalset energiat väljendav liige lisada potentsiaalset energiat väljendav liige
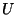 . .
Asendades teist järku tuletise 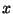 järgi Laplace'i
operaatoriga järgi Laplace'i
operaatoriga
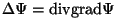 , saame kokku , saame kokku
ning pärast 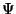 -ga korrutamist -ga korrutamist
|
|
|
mis ongi Schrödingeri võrrandi üldkuju.
|
Kui lisada kineetilisele ka potentsiaalne energia, saadakse osakese liikkumisvõrrand jõuväljas.
|
|
Peame kohe ütlema, et mingeid üldiseid meetodeid selle võrrandi
lahendamiseks pole. Lihtsamail juhtudel (välisjõudude puudumine,
ajas muutumatu väli) saab lahendeid muidugi leida.
Õnneks
pole meil lainefunktsiooni endaga midagi peale hakata. Asi, mis
meid huvitab, on interferentspildi ajalis-ruumiline käik,
st. lainefunktsiooni amplituudi muutumine.
Kompleksmuutuja
teooriast on teada, et amplituudi määrab 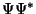 (
(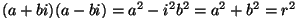 , kus , kus 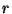 on kompleksarvu
moodul geomeetrilisest kujust); laine "sagedus" pole üldse
oluline. on kompleksarvu
moodul geomeetrilisest kujust); laine "sagedus" pole üldse
oluline.
Niisiis oleks hea ajas muutuvast osast vabaneda.
Kirjutame lainevõrrandi ümber:
|
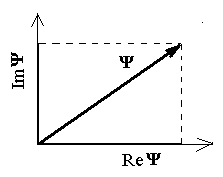
Faasidiagramm phasor komplekstasandil.
Mooduli ruut (laine amplituud) on 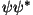
|
|
See on lainefunktsiooni hetkväärtuse valem.
|
See, mida otsime, on ruumiline seisevlaine 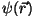 ,
mille amplituudi maksimum ,
mille amplituudi maksimum 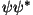 näitab meile
osakese asukohta. Proovime eraldada lainevõrrandist võnkumise
ajalise komponendi ja seejärel uurida amplituudi väärtust
ruumifunktsioonina. näitab meile
osakese asukohta. Proovime eraldada lainevõrrandist võnkumise
ajalise komponendi ja seejärel uurida amplituudi väärtust
ruumifunktsioonina.
Pannes kaheosalise lainefunktsiooni
Schrödingeri võrrandisse ja eeldades, et 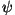 ajaline tuletis
on null, saame ajaline tuletis
on null, saame
|
|
|
Hetkväärtuse tuletis aja järgi
|
Viimase teguri kordaja
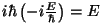 ning koondades võrrandist ajas muutuva eksponendi, saame
statsionaarse oleku võrrandi
ning koondades võrrandist ajas muutuva eksponendi, saame
statsionaarse oleku võrrandi
|
|
|
|
Statsionaarse oleku võrrand
|
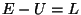 on meile mehaanikast tuttav Lagrange'i funktsioon. on meile mehaanikast tuttav Lagrange'i funktsioon.
Saadud võrrandil on kaks võimalikku lahendit:
eksponentfunktsioon, kui 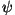 kordaja on negatiivne ja
ruumis harmooniliselt muutuv funktsioon (siinus, koosinus), kui
kordaja on positiivne. kordaja on negatiivne ja
ruumis harmooniliselt muutuv funktsioon (siinus, koosinus), kui
kordaja on positiivne.
|
|
Et otsime lainefunktsiooni, siis
kõlbab meile vaid teine võimalus.
Selleks peab olema 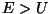 , mis
tähendab vaba osakest, millel on piisavalt energiat jõuväljast
väljumiseks. , mis
tähendab vaba osakest, millel on piisavalt energiat jõuväljast
väljumiseks.
Kui 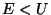 , on enamikel juhtudel lainefunktsioon määramatu. , on enamikel juhtudel lainefunktsioon määramatu.
Erandi moodustavad kindlad energiatasemed, kus lainefunktsioon
on võimalik nullist erineva amplituudiga seisevlainena.
Energia selliseid väärtusi nimetatakse võrrandi
omaväärtusteks ja vastavaid lainefunktsioone
omafunktsioonideks.
Omaväärtuste ja -funktsioonide leidmise
näiteid vt. Saveljev, Füüsika III, lk 247 - 254.
|
Seotud elektroni lainevõrrand omab lahendit vaid kindlate energiate korral
Kas saite jagu?
|
|
Lainemehaanika rakendusi.
Ühe-elektroni-üleminekud. Tuleme tagasi oma
põhiprobleemi - aatomi kiirgusspektri juurde. Nüüd teame, et
pannes Schrödingeri võrrandisse elektroni potentsiaalse energia
aatomituuma väljas, saame omaväärtustena energiatasemed.
Et väli on tsentraalsümmeetriline, on otstarbekas kasutada
sfäärilisi koordinaate. Laplace'i operaator 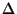 koosneb
nagu kolmruumile kohane kolmest liikmest, mistõttu kogu võrrand
saab kuju koosneb
nagu kolmruumile kohane kolmest liikmest, mistõttu kogu võrrand
saab kuju
|
Punktlaengute tsentraalsümmeetrilise välja korral kasutab nii tavaline kui kvantmehaanika sfäärilisi koordinaate.
|
Kolm kvantarvu. Omaväärtusprobleemi lahend sõltub nüüd välja sümmeetriast.
Üldjuhul peaks kvant-tingimus
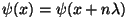 kehtima kõigi kolme vabadusastme
(
kehtima kõigi kolme vabadusastme
(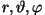 ) korral. ) korral.
Seega
tuleb meil mängu koguni kolm kvantarvu;
aatomifüüsikas
tähistatakse neid tähtedega 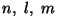 ja nimetatakse vastavalt
peakvantarvuks ( ja nimetatakse vastavalt
peakvantarvuks (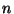 ),
orbitaalseks kvantarvuks ( ),
orbitaalseks kvantarvuks (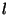 )
ja
magnetiliseks kvantarvuks ( )
ja
magnetiliseks kvantarvuks (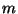 ).
Iseasi, kas neile ka
energianivoosid vastab.
Kui ).
Iseasi, kas neile ka
energianivoosid vastab.
Kui 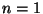 ("orbiidil üks lainepikkus"),
ei anna "laine pööramine" ("orbiidil üks lainepikkus"),
ei anna "laine pööramine" 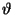 või või 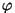 sihis midagi; sihis midagi;
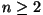 puhul aga saame juurde täiendava laine. puhul aga saame juurde täiendava laine.
|
Perioodilisust märkivad täisarvulised kordajad kannavad lainemehaanikas kvant-arvude nime.
|
|
Piltlikustamise eesmärgil loetakse orbitaalset (mõnikord
nimetatakse ka asimutaalseks, kuna 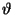 on asimuutnurk)
kvantarvu elektroni impulssmomendi (pöörlemishulga)
kirjeldajaks. Seega on ka impulssmoment kvanditud, ning samuti
tema projektsioonid etteantud teljele - viimaseid mõõdab siis
magnetiline (polaarne?) kvantarv on asimuutnurk)
kvantarvu elektroni impulssmomendi (pöörlemishulga)
kirjeldajaks. Seega on ka impulssmoment kvanditud, ning samuti
tema projektsioonid etteantud teljele - viimaseid mõõdab siis
magnetiline (polaarne?) kvantarv 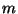 . Kokku on statsionaarne
olek määratud siiski energiaga ja tsentraalsümmeetrilise välja
korral sõltub see vaid peakvantarvust . Kokku on statsionaarne
olek määratud siiski energiaga ja tsentraalsümmeetrilise välja
korral sõltub see vaid peakvantarvust 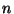 . Nii on lood
vesinikuaatomis. . Nii on lood
vesinikuaatomis.
Leelismetallide korral on pilt erinev. Ka siin toimuvad
üleminekud üheainsa (valents)elektroni orbiidi muutuste kaudu.
Et aga erinevalt vesinikust on väli mõjutatud ka teiste,
"sisemiste" elektronide poolt, pole energiatasemed orbitaalse
kvantarvu 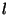 eri väärtustel enam samad. eri väärtustel enam samad.
Seda näitavadki
parandid Rydbergi valemites. Magnetiline kvantarv 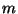 aga jääb
varjatuks seni, kuni ruumiteljed on energeetiliselt samaväärsed. aga jääb
varjatuks seni, kuni ruumiteljed on energeetiliselt samaväärsed.
Tarvitseb meil aga "sisse lülitada" väline (makroskoopiline)
elektri- või magnetväli, kui asi muutub. Tekib elektroni
"orbiidi pretsessioon" (jälle klassikalise füüsika keeles!),
salvestub täiendav energia ja energianivood lõhestuvadki
vastavalt magnetkvantarvule.
Vastavat muutust spektris nim.
Starki (elektriväli) või Zeemani (magnetväli) efektiks.
Neljas kvantarv - spin. Kui spektrograafide
lahutusvõime jõudis kümnendiku nanomeetrini, selgus, et enamik
jooni koosneb mitmest lähestikku asuvast komponendist. Seega
peab eksisteerima veel üks energia salvestamise võimalus.
|


Zeemanni efekt.
Päikeselaigu magnetväli (ülemisel pildil) lõhub spektrijoone kolmeks eri lainepikkusega komponendiks.
|
|
1925. a. esitasid S. Goudsmit ja G. Uhlenbeck hüpoteesi, et ka
elektronil on pöörlemisenergia. Kui elekroni omaimpulssmoment
ühtib tema orbitaalse liikumise impulssmomendiga, on energia
suurem kui juhul, kus momendid on vastassuunalised.
Omaimpulssmomenti nimetati spin'iks (ingl. spin -
pöörlema, ka värten) ja see oli juba olemuselt kvanditud (kas
üht või teistpidi). Talle omistati kvantarv 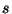 , mis erinevalt
teistest omas murdväärtust , mis erinevalt
teistest omas murdväärtust
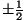 . .
|
Elektroni pöörlemissuund annab neljanda kvantarvu - spinni.
|
|
Schrödingeri võrrandist, kus Laplace'i operaator koosneb kolmest
liikmest, pole neljandat kvantarvu kusagilt võtta. Aga
1920-datel aastatel oli hästi teada, et harjumuspärane
eukleidiline kolmruum pole sugugi ainus (ega isegi mitte parim)
võimalus füüsikaliste nähtuste kirjeldmiseks.
Elektrodünaamika
ja relatiivsusteooria neljamõõtmeline aegruum, kus kolmele
ruumikoordinaadile lisandub 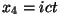 ( (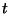 on tavaline
ajakoordinaat), saab lainevõrrand kuju on tavaline
ajakoordinaat), saab lainevõrrand kuju
kus  on Laplace'i operaatori on Laplace'i operaatori 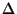 4-mõõtmeline
analoog, 4-mõõtmeline
analoog,
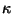 vastab lainearvule ja avaldub vastab lainearvule ja avaldub
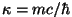 ,
mass ,
mass 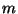 on relativistlik, st. sisaldab
lisaks "tavalisele" seisumassile ka koguenergia. on relativistlik, st. sisaldab
lisaks "tavalisele" seisumassile ka koguenergia.
Et  koosneb neljast liikmest, on ka omaväärtuste komplekte
neli ja spinkvantarv
koosneb neljast liikmest, on ka omaväärtuste komplekte
neli ja spinkvantarv 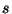 sobib hästi Schrödingeri kolmiku
täienduseks. sobib hästi Schrödingeri kolmiku
täienduseks.
|
Spinni lisamine muudab pildi neljamõõtmeliseks ("aegruumiliseks").
|
|
Kokkuvõttes saame tuuma ümber
tiirlevast üksikust elektronist järgneva pildi:
Sümmeetrilises
väljas määrab energiataseme paar 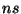 ,
ebasümmeetrilises kolmik ,
ebasümmeetrilises kolmik
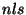 ja
välise (magnet)välja olemasolul kogu nelik ja
välise (magnet)välja olemasolul kogu nelik 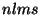 . .
|
|
|
Vastavalt energiatasemetele kujunevad ka üleminekud; spekter
tuleb seda keerukam, mida rohkem on tasemeid. Et jooni siiski
lõplik arv on, seda tingivad mõned lainekontseptsioonist
tulenevad jäävusseadused.
|
|
|
Määramatuse relatsioon. Elektronile lainepikkuse omistamine
ja tema asukoha sidumine seisevlaine maksimumidega tähendab, et
asukoht on määratav lainepikkuse täpsuseni. Samasuguse tõlgenduse
võib anda ka Planck'i energiakvandile: ülekantav energiahulk määrab
minimaalse ajavahemiku (perioodi), mille vältel on ülekanne
võimalik.
1927. aastal andis saksa füüsik Werner Heisenberg neile valemitele
kuju, mis on tänapäeval tuntud määramatuse relatsiooni nime all:
|
Heisenbergi määramatuse printsiip (relatsioon) seob osakese asukoha ruumis tema kiirusega, ajamomendi aga energiaga.
Mõlema täpsusele paneb piiri kvanttingimus.
|
Suurusi 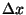 , , 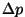 , , 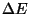 ja ja 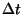 võib
käsitleda kui tavalisi mõõtmisvigu. Määramatuse printsiip ütleb,
et teatud väikesed vead on loodusseadustesse "sisse kirjutatud", nad
on omaette loodusseadus. Filosoofilistes tõlgendustes
räägitaksegi tavaliselt "mõõtmistäpsusest". Tavaväide on
järgmine: mida täpsemalt püüame määrata impulssi (energiat), seda
ebatäpsemaks muutub asukoht (aeg). võib
käsitleda kui tavalisi mõõtmisvigu. Määramatuse printsiip ütleb,
et teatud väikesed vead on loodusseadustesse "sisse kirjutatud", nad
on omaette loodusseadus. Filosoofilistes tõlgendustes
räägitaksegi tavaliselt "mõõtmistäpsusest". Tavaväide on
järgmine: mida täpsemalt püüame määrata impulssi (energiat), seda
ebatäpsemaks muutub asukoht (aeg).
Kvanditud faasiruum. Füüsikud ise suhtuvad määramatuse
relatsiooni kui võimalusse tuua lisaks Newtoni "pidevale ruumile"
valemeisse "tükiline" kvantruum, kus asukoht-impulss on
määratud kvantarvudega. Aga - see on teostatav ainult sellises
(matemaatilises) ruumis,
kus nii asukoht kui impulss
on võrdõiguslikud ruumikoordinaadid.
Teoreetilises mehaanikas
nimetatakse selliseid ruume faasiruumideks.
Omal ajal olid
nad kasutusel kui arvutuslik abivahend - nende abil sai liikumist
kirja panna lineaarsete diferentsiaalvõrrandite abil, kasutamata
teist järku tuletisi.
Kui klassikalise mehaanika faasiruum oli pidev, siis kvantfüüsikas
koosneb see ühesuguse servapikkusega "kastikestest". Iga sellise
kuubikujulise kasti sisse võib panna ühe või mitu osakest, mis
kvantmehaanika koha pealt omaksid ühesuguseid (faasi)ruumi
koordinaate.
Kui võtta ruumikoordinaatidele lisaks ka aeg, saame klassikalises
füüsikas nn. aegruumi - mille neljandaks koordinaadiks on
ajavahemiku 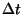 jooksul valguse poolt läbitud vahemaa jooksul valguse poolt läbitud vahemaa 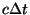 . Ka faasiruumis on ajakoordinaat olemas, energia . Ka faasiruumis on ajakoordinaat olemas, energia 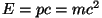 kujul. Valemit
kujul. Valemit
|
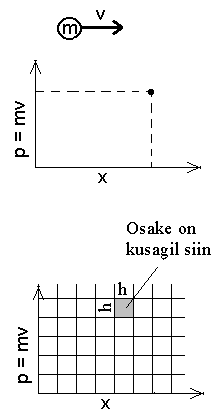
X-telge pidi liikuva osalese asukoht faasiruumis
klassikalise (ülal) ja
kvantmehaanika (all) tõlgenduses.
|
seostatakse tavaliselt Einsteini relatiivsusteooriaga ja nimetatakse
massi ning energia ekvivalentsuse seaduseks.
Kui aga käsitleda energialiiget faasiruumi täiendava (nüüd juba
kaheksanda!) koordinaadina, saame kokku kaheksamõõtmelistest
kastikestest koosneva diskreetse (mittepideva) matemaatilise ruumi
See ongi uue ajastu füüsikute matemaatiline mängumaa. Kohe näete,
mida tema abiga korda võib saata.
Pauli keeld ja kvantstatistika
Naatriumi spektri kirjeldamisel jätsime põhjendamata
spektraaltermide lähtumise peakvantarvu väärtusest 3. See, et
tegu on ühe elektroniga paljudest - valentselektroniga - sai
ära öeldud; põhjus, miks ei või 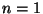 või 2, jäi selgusetuks. või 2, jäi selgusetuks.
Mendelejevi tabel. Keemiliste elementide perioodilisuse süsteemi avastas
D. Mendelejev 1869. a. 1920-dateks aastateks oli keemias välja
kujunenud elektroonne valentsiteooria, mille järgi omaduste
perioodilisuse põhjuseks oli "maagiline arv" kaheksa (rühmade
arv perioodis). Kui Goudsmit ja Uhlenbeck tulid välja neljanda
kvantarvuga, selgus, et perioodide teket saab kirja panna kolme
lihtsa reegliga:
|
|
- Elektroni põhiseisundiks aatomis on minimaalse
energiaga seisund (potentsiaalse energia miinimumi lause)
- Elektroni energia on seda suurem, mida suurem on
kvantarvude summa
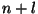 ; kui need on võrdsed, vastab suurem
energia ; kui need on võrdsed, vastab suurem
energia 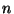 suuremale väärtusele (Kletškovski reegel). suuremale väärtusele (Kletškovski reegel).
- Aatomis ei saa olla kaht elektroni, millel oleks
samasugune kvantarvude nelik (Pauli keeluprintsiip).
Lihtsuses peitub ilu, ja nende reeglite vastavus tegelikkusele
on vapustav. Aatomi elektronkate on
kihilise ehitusega: kvantarvude paarile 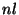 vastavad
allkihid täituvad kindlas järjekorras; orbitaalse kvantarvu vastavad
allkihid täituvad kindlas järjekorras; orbitaalse kvantarvu 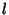 väärtustele 0 ja 1 vastavad allkihid, sisaldades kokku alati 8
või vähem elektroni, määravad elemendi rühma, koos sellega
ka valentsi. Perioodi määrab välimise katte
peakvantarv
väärtustele 0 ja 1 vastavad allkihid, sisaldades kokku alati 8
või vähem elektroni, määravad elemendi rühma, koos sellega
ka valentsi. Perioodi määrab välimise katte
peakvantarv 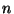 ; elementide arvu perioodis aga pärast
peakvantarvu suurenemist lisandunud elektronide arv. ; elementide arvu perioodis aga pärast
peakvantarvu suurenemist lisandunud elektronide arv.
|
Keerulisemates aatomites jagunevad elektronid sama peakvantarvuga kihtidesse - elektronkatetesse.
Elemendi keemilised omadused (valentsi) määrab välimise kihi täidetus.
Elektronkatete täitumise järjekorra määravad potentsiaalse energia miinimumi lause, Kletskovski reegel ja Pauli keeluprintsiip.
|
|
|
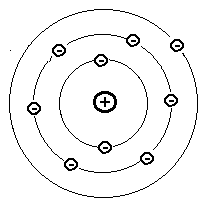
Naatriumi aatomi skeem:
kaks alumist kihti (n = 1 ja n = 2) on täidetud, kihis n = 3 on üks elektron.
|
|
Joone kohal Mendelejevi tabel katkeb: raskeim looduslik element uraan
sisaldab 92 elektroni. Tuumareaktorite ning kiirendite abiga on
"juurde tehtud" veel 22 tehiselementi, millede tuumad on paraku liig
lühikese elueaga (sellest järgmises loengus), et nendega keemilisi
reaktsioone läbi viia.
Et kõrgemad energianivood eksisteerivad, seda näitab vastavate
spektrijoonte olemasolu. Ainult et sinna ei jätku elektrone.
|
|
|
Pauli printsiibi põhjenduse saame lainefüüsikast.
Tegelik teooria on meile matemaatiliselt kättesaamatu, kuid
R. Feynmann on andnud ilusa piltliku seletuse, mis üsna hästi
haakub E. Fermi ja P. Dirac'i poolt 1940. a. tehtuga.
Kujutame "kahe osakese kohtumist". Kui nad on harjumuspärased
makrokehad, võime nad enda jaoks ära märkida (värvida,
nummerdada, nimetada) ning pärast kohtumist teame täpselt,
milline osake kuhu läks. Kui on aga tegemist lainefunktsiooniga,
ei saa me sarnaste osakeste korral öelda, millisele nimelt
vastab vaadeldav laine(funktsiooni) amplituud. Seega on osakesed
eristamatud ja piltide a) ja b) vahel pole võimalik vahet
teha.
Lainemehaanika keeles on a) ja b) võrdtõenäosed sündmused
ja nende lainefunktsioonidel peab olema sama amplituud.
Tähistades esimese osakese sattumise ülemisele positsioonile
lainefunktsiooniga 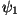 ja teise sattumise samasse kohta ja teise sattumise samasse kohta
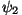 , võime seega öelda, et , võime seega öelda, et
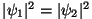 . Kui
lähtuda lainefunktsiooni standardkujust . Kui
lähtuda lainefunktsiooni standardkujust
|
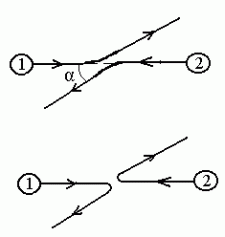
Elektronide põrge Feynmanni järgi.
Ülemisel graafikul on hajumisnurk 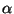 ,
alumisel 180° + ,
alumisel 180° + 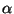 . .
Kvantteooria järgi on neid kahte võimatu eristada.
|
kus 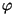 on faasinurk, tähendab on faasinurk, tähendab 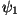 ja ja 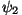 keskväärtuste võrdsus amplituudide võrdsust, millele oskeste
eristamatus lisab veel laineparameetrite
keskväärtuste võrdsus amplituudide võrdsust, millele oskeste
eristamatus lisab veel laineparameetrite
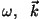 võrdsuse. Ainus asi, mis pole fikseeritud, on faasinurk ja
seetõttu saavad meie kaks lainefunktsiooni erineda vaid nn.
faasikordaja
võrdsuse. Ainus asi, mis pole fikseeritud, on faasinurk ja
seetõttu saavad meie kaks lainefunktsiooni erineda vaid nn.
faasikordaja
võrra:
Faasikordaja leidmiseks kujutame nüüd eelmisel joonisel olevat
protsessi kahekordsena.
Ülemisel joonisel on põrked toimunud osakeste vahetuseta,
alumisel toimub vahetus mõlemal põrkel. Tulemus on ekvivalentne,
seega on nüüd protsesside lainefunktsioon sama. See tähendab, et
millest 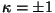 . .
|
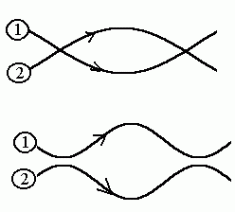
Kaksikpõrge. Alg- ja lõppseisundid on mõlemal juhul ekvivalentsed, ülemisel joonisel toimub vahepeal osakeste vahetus.
Faasiteguri väärtus +1 tähendab lainefunktsioonide liitumist samas faasis (bosonid),
-1 tähendab liitumist vastasfaasis (fermionid).
|
|
Toodud kaalutlus, ehkki "mittematemaatiline", näitab, et
osakese faasikordaja võib omada väärtusi 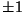 . .
Esimene
võimalus (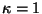 ) vastab faasinurgale ) vastab faasinurgale
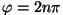 , kus
n=0, 1, 2... - osakeste lainefunktsioonid on samas faasis.
Teisel juhul , kus
n=0, 1, 2... - osakeste lainefunktsioonid on samas faasis.
Teisel juhul
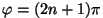 ja me võime öelda, et osakesed
"liituvad vastasfaasis". ja me võime öelda, et osakesed
"liituvad vastasfaasis".
Bosonid ja fermionid. Fermi ja Dirac väitsid, et
faasikordaja tüüp sõltub osakete tüübist. Nii saame
footonite liitmisel seda intensiivsema spektrijoone, mida
rohkem meil on samade parameetritega footoneid - niisiis
on footon esimest tüüpi osake. Teame, et footonite
tasakaaluline statistiline jaotus on Plancki "musta keha valem",
seega vastab neile jaotus
Seda jaotust nimetatakse kvantstatistikas Bose-Einsteini
jaotuseks ning sellele alluvaid osakesi bosoniteks.
Liites teist tüüpi osakesi, märkame, et samade parameetritega
lainefunktsioonid kustutavad teineteist. Seetõttu polegi
võimalik rohkem kui ühe samade parameetritega (asukoht, impulss,
energia) osakeste üheaegne eksisteerimine.
Et näiteks asukoht ja
impulss on Heisenbergi määramatuse relatsiooni järgi määratud
vaid Plancki konstandi täpsusega, ei saa neid lõpmata tihedalt
pakkida - igaühel on
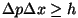 , seega võtab ta
faasiruumis , seega võtab ta
faasiruumis
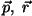 enda alla "kuubi" ruumalaga enda alla "kuubi" ruumalaga
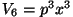 . (Indeks "6" tähendab, et faasiruum on
kuuemõõtmeline.) . (Indeks "6" tähendab, et faasiruum on
kuuemõõtmeline.)
|
|
|
See muudab ka statistilise jaotuse:
mis kannab nime Fermi-Dirac'i jaotus.
Osakesi, mis
alluvad Pauli keelule, nimetatakse fermionideks.
|
Fermionide korral kustutab juurdetulev lainefunktsioon eelmise (kui see on olemas). See tähendab, et faasiruumi rakus ei saa olla rohkem kui üks osake.
|
Võrdleme saadud jaotusfunktsioone klassikalisest füüsikast
tuntud Boltzmanni jaotusega:
Näeme, et see vastab mõlema ülaltoodud jaotuse piirjuhule
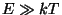 - siis ei oma liidetav - siis ei oma liidetav 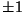 nimetajas enam tähtsust.
Vastupidisel juhul, kus nimetajas enam tähtsust.
Vastupidisel juhul, kus
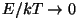 , on antud energiaga
bosonite arv kuitahes suur
( , on antud energiaga
bosonite arv kuitahes suur
(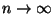 ), fermionide
oma aga piiratud. ), fermionide
oma aga piiratud.
Vabade osakeste korral määrab see osakeste
maksimaalse ruumtiheduse antud temperatuuril; aatomis, kus
energiatasemed on diskreetsed, aga elektronide maksimaalse
lubatud arvu vaadeldavas kihis.
Muide, asjaolu, et elektronid
ei allu klassikalisest mehaanikast tuletatud Maxwelli jaotusele,
on ka metallide elektrijuhtivuse klassikalise elektronteooria
puuduste põhjuseks. Kvantparandi sisseviimine kõrvaldab näiteks
vastuolu eritakistuse sõltuvuses temperatuurist
(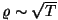 klassikalises teoorias pro klassikalises teoorias pro 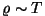 empiirilises
valemis). empiirilises
valemis).
Elektronkihi energiatasemed.
Mitme elektroni samaaegne asumine ühel ja samal energianivool
muudab ka spektraaltermi mõtet. Kuna me nagunii ei tea, millise
elektroniga toimub muutus, on mõttekam jälgida mitte igat
üksikut elektroni, vaid kogu aatomi energeetilisi parameetreid.
|
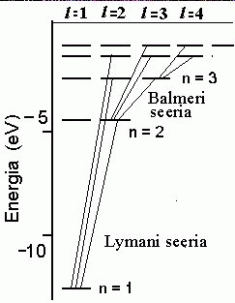
Energianivood vesinikuaatomis.
Kuna elektroni energia sõltub vaid pea-kvantarvust n, tekivad lihtsad, tihenevate joontega seeriad.
|
|
Tavaliselt piirdub üleminek küll ainult valentskihi muutusega;
vähemalt rakendatakse seda eeldust optiliste spektrite
korral. (Röntgenijooned seevastu tekivad just üleminekul
alumistes kihtides ja neid nimetataksegi vastava kihi järgi,
näiteks K-joon jne.) Et valentselektronidel on sama
peakvantarv, lähtutakse termi kirjapanekul ülejäänuist -
orbitaalsest ja spinkvantarvust.
Liitmine vektormeetodil. Oletame, et orbitaalne
kvantarv vastab elektroni orbitaalsele impulssmomendile. Et
viimane on vektor, tuleb elektronkihi kogumomendi leidmiseks
summeerida vektorid; seejuures peab summaks saadav kvantarv
olema positiivne täisarv.
Kuna vektorite suunad on erinevad,
saame summeerimisel kõik täisarvud minimaalse absoluutväärtusega
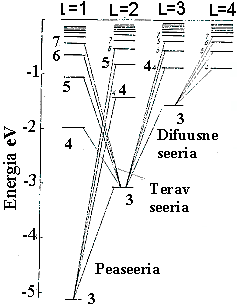
kombinatsioonist (kahe elektroni korral  , kolme või
enama puhultuleb kombineerida) kuni summani , kolme või
enama puhultuleb kombineerida) kuni summani
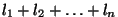 . .
Need on kihi orbitaalkvantarvu võimalikud väärtused;
tegelikud saame pärast Pauli keeluga keelustatud
kombinatsioonide kõrvaldamist.
|
Naatriumi aatom.
Energianivood on lõhustunud vastavalt orbitaal-kvantarvu väärtusele. Spektrijooned on koondunud rühmadesse.
|
|
Sama meetodit kasutame spinide liitmisel. Et spini väärtus on
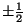 , on siin asi lihtsam: , on siin asi lihtsam:
paarisarv elektroni korral
on
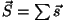 ja ja
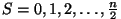 - kõik
täisarvud;
paaritu arvu korral aga - kõik
täisarvud;
paaritu arvu korral aga
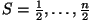 - kõik poolarvud. - kõik poolarvud.
Jääb üle liita vektorid 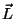 ja ja 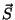 . Et ka see summa
peab olema täisarvuline, saame siingi reegli . Et ka see summa
peab olema täisarvuline, saame siingi reegli
Termi tähis. Et orbitaalne impulssmoment on võrratult
suurem spinorbitaalsest, määrab energiataseme eelkõige 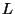 . See
valitaksegi termi tähiseks; kasutatakse nagu ühe elektroni
korral ajaloolisi tähtsümboleid s(harp), p(rincipal) jne. selle
vahega, et elektronkihi summaarset orbitaalkvantarvu
tähistab suur täht ( . See
valitaksegi termi tähiseks; kasutatakse nagu ühe elektroni
korral ajaloolisi tähtsümboleid s(harp), p(rincipal) jne. selle
vahega, et elektronkihi summaarset orbitaalkvantarvu
tähistab suur täht (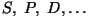 ). ).
|
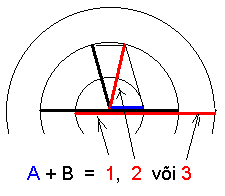
Kahe valentselektroniga aatomi energianivoode leidmiseks liidetakse orbitaal-kvantarvud vektormeetodi järgi.
NB!Summa peab olema kvanditud, st. täisarvuline.
|
|
Indeksiteks on
spinkvantarvust 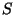 sõltuv multipletsus sõltuv multipletsus 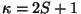 ja
alamtaset väljendav kvantarv ja
alamtaset väljendav kvantarv 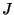 . .
Nii saame kahe elektroni
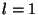 , , 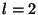 liitumisel kuus võimalikku termi: liitumisel kuus võimalikku termi:
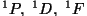 , kui , kui 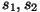 on vastasmärgilised; on vastasmärgilised;
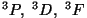 , kui , kui 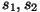 on samamärgilised. on samamärgilised.
Ülemise rea korral asi sellega piirdub, alumise rea termid
jagunevad veel kolmeks tasemeks (tasemete arv vastab
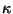 väärtusele). Seega on meil esimese rea viimane liige
singletne term väärtusele). Seega on meil esimese rea viimane liige
singletne term 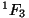 , alumises reas aga tripletne
term tasemetega , alumises reas aga tripletne
term tasemetega 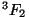 , , 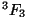 , , 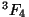 . .
Aga vast aitab. Kui näete kusagil selliste tähistega valemeid, siis
teate, kuhu oleta sattunud.
|
|
|
Molekulide ja kristallide spektrid.
Et enamus ainetest ei koosne mitte aatomitest, vaid
molekulidest, peab seegi leidma oma kajastuse kvantteoorias. Nii
ka on, ainult et molekuli lainefunktsiooni pole seni keegi
välja arvutanud. Kiirgusspektri omadused on seevastu hästi teada
ja vastavalt sellele on tehtud ka ligikaudsed teooriad:
- Molekuli komponente (tuumad, ioonid) vaadeldakse kui
iseseisvaid aatomeid naaberiooni(de) väljas. Tulemuseks on
häiritud atomaarspekter, mis päris hästi vaadeldavaga kokku
langeb.
- Molekuli vaadeldakse kui kahest või mitmest ioonist
koosnevat vibraatorit, kus ioonide vastasmõju energianivood
liituvad atomaarsetele termidele. Sellest variandist tuleneb
lõhestunud atomaarsete nivoode nimetamine pöörlemis- ja
võnkenivoodeks. Tüüpiline energiate vahe pöörlemisspektris
on
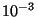 eV, st. umbes 10000 korda väiksem elektroonsete
termide omast; võnkespekter (0.1 eV) asub vahepeal. eV, st. umbes 10000 korda väiksem elektroonsete
termide omast; võnkespekter (0.1 eV) asub vahepeal.
|
Aatomikoosluste (molekulid, kristallid) energiaseisundite arvutamisel kasutatakse häiritusarvutust.
|
|
Pöörlemis- ja võnkenivoode tõttu on molekuli spektris atomaarse
joone asemel riba, mis omakorda koosneb
võnkeenergianivoode poolt eraldatud pöörlemisjoonte gruppidest.
Madala lahutusvõimega spektraalriistas paistab see joonte
müriaad ühtlase ribana, mistõttu teda algselt nimetatigi
ribaspektriks.
Arusaadavalt käib see jutt hõreda
mitmeaatomilise gaasi kohta; vedelates ja tahketes kehades
tulevad mängu veel täiendavad vastasmõju liigid.
|

Lämmastiku ribaspekter.
|
|
Kondenseerunud aine.
Spektrist pole siin midagi uut rääkida - see on kiirgusoptikast
hästi tuntud Planck'i musta keha kiirgus. Siiski mitte alati:
ärge unustage luminestsentsi! Mida ütleb selle kohta kvantfüüsika?
Kui ka siin rakendada häiritusarvutust, saame eelnevale punktile
sarnase tulemuse. Ainult et häirituse allikas pole nüüd
kindlal kaugusel asuv naabertuum, vaid kõigi naaberaatomite ja
-molekulide kogum. Seetõttu ei jagune atomaarne nivoo mitte
kümneks-viieteistkümneks, vaid tuhandeteks ja miljoniteks
alamnivoodeks, mis kõik asuvad kindlas, lähimate naabrite
kaugustega määratud ribas.
Sellist laiaksvenitatud energianivood
nimetatakse tahkisefüüsikas tsooniks; tsooni laius
vastab siis häirituse tugevusele ning tsoonide vahekaugus
atomaarsete nivoode vahelisele kaugusele. Kui häiritus on tugev
ja energianivoode vahe väike, võivad tsoonid kattuda; tavaliselt
tekib siiski igast nivoost oma tsoon, mida eraldab
naabertsoonidest "keelatud energiate piirkond" -
keelutsoon. Keelutsooni laius ja tsoonide täidetus
elektronidega määrabki aine makrofüüsikalised parameetrid, nagu
elektri- ja soojajuhtivus.
|
|
|
Elektrijuhtivuse kvantteooria. Normaalolekus on aatomite alumised elektronkatted täidetud ning
täitmata kihi elektronid põhiseisundis. Nii tekib aine
omadustest sõltuv tsoonide jaotus, kus madala energiaga
täidetud tsoonidele järgneb pärast keelutsooni vaid osaliselt
elektronidega täidetud valentstsoon. Valentstsooni
elektronid, olles aatomitega nõrgalt seotud, moodustavad kogu
kristallile (vedelikule) ühise elektrongaasi, mis võib
ainetüki piires suhteliselt vabalt liikuda ning, kandes
elektrilaengut, muuta aine elektrit juhtivaks. Vabad elektronid
kannavad ka kineetilist energiat, põhjustades näiteks metallide
hea soojusjuhtivuse.
Kui täidetud on kõik elektronkatted (näiteks liitainetes),
pole valentstsooni elektrone üldse olemas. Sellistes ainetes on
kõik elektronid aatomitega seotud ja ehkki ka täidetud tsoonid
võivad olla küllalt laiad, ei pääse elektronid liikuma. Nii
tekivad elektrit (ja soojust) mittejuhtivad ained -
dielektrikud. Tihti on ka selliste ainete kiirgus
mittetasakaaluline, kuna elektronide ergastamine täidetud
tsoonist on seotud küllalt suurte energiatega. Paljudes
luminofoorides tekibki ergastus vaid väga suure energiaga
kvantide või osakest mõjul.
Kõige huvitavam on juhtum, kus elektron saab suhteliselt kitsast
(vastab väikesele energiate vahele) keelutsooni
ületada juba üsna väikese lisaenergia olemasolu korral. Et
molekulide tasakaaluline kiiruste jaotus katab üsna suure
kiiruste vahemiku, võib mõni kiirem elektron vabalt "keelu"
ületada ja sattuda (tühja) valentstsooni. Seal muutub ta otsemaid
"vabaks elektroniks", mis käitub analoogiliselt elektrijuhtide
valentstsooni elektronidega. Veelgi enam - täidetud tsoonist
"ärakadunud" elektron jätab järele laengu puudujäägi - nn.
augu millesse võivad liikuda naaberelektronid. Kui selline
pooljuht asub elektriväljas, tekib lisaks liikuvatele
elektronidele ka aukude suunatud triiv, mida võib samuti
käsitleda elektrivooluna.
|
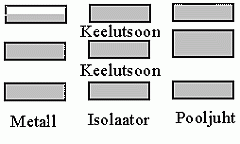
Kristalli elektrilised omadused
(tsooniteooria kohaselt):
osaliselt täidetud valentstsoon kindlustab elektronjuhtivuse (metallid), täidetud tsooni korral sõltub juhtivus keelutsooni laiusest
(isolaator või pooljuht).
|
|
Et pooljuhtide elektrijuhtivus sõltub vabade elektronide arvust,
viimane omakorda paljudest välisteguritest, on just pooljuhtidel
tänapäeva tehnoloogias määratu tähtsus. Pooljuhtseadmed lubavad
mõõta paljusid suurusi (temperatuur, valgustatus) elektriliselt,
mõõtes uuritavasse keskkonda pandud pooljuhi takistust. Veelgi
enam: pooljuhtide omadused lubavad neid kasutada elektroonikas
elektrivoolu parameetrite suunamiseks. Võrreldes vaakumtehnikaga
on pooljuhtseadmed tuhandeid kordi väiksemad, nende voolutarve
on minimaalne ja töökindlus praktiliselt piiramatu.
|
|
|
Kvantgeneraator. Lõpetame atomaarse kiirguse jutu
väikese mõistatusega. See, et aatom, neelanud kvandi energiaga
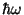 , läheb üle suurema energiaga nivoole , läheb üle suurema energiaga nivoole
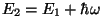 , on arusaadav. Lisaks sellele võib aga
toimuda protsess , on arusaadav. Lisaks sellele võib aga
toimuda protsess
kus juba varem ergastatud aatom pealelangeva kvandi mõjul
kiirgab samasuguse, neelatuga identse kvandi.
Sellist protsessi nimetatakse indutseeritud kiirguseks ja
ta avastati sajandivahetuse spektraaluuringute käigus. Tavalises
olukorras on indutseeritud üleminekute arv väike (aatomid on
valdavalt põhiseisundis) ning kiirguse võimendumine tühine. Asi
muutus, kui avastati nn. metastabiilsed seisundid, kus
aatomite üleminek ergastatud seisundist põhiseisundisse on
blokeeritud mingi valikureegli tõttu.
Metastabiilses ergastatud seisundis võib aatom olla
suhteliselt kaua (kosmilistes gaasududes, kus hõreda aine tõttu
mõjustusi vähe, isegi aastaid); aga üleminek toimub alati, kui
ergastatud aatom kohtub tema energiavahele vastava kvandiga.
See kätkeb endas valguse võimendamise võimalust, mis 1953. a. ka
realiseeriti.
Kuidas? Tuli kasutada kaudset ergastust: gaas või
kristall paigutati lühemalainelise kiirguse välja nii, et osa
ergastatud aatomeid sattusid pärast väikese energiaga kvandi
kiirgamist metastabiilsele energianivoole. Kui nüüd lasta
sellisele gaasile üks "õige" footon, algabki indutseeritud
kiirgus, mis kestab seni, kuni energianivoode normaalne
asustatus on taastatud. Et genereeritavad footonid on identsed
(samasuunalised ja samas faasis algfootoniga), tekib raadiolaine
sarnane teravalt suunatud ja rangelt koherentne (mida tähendab?)
kiirgus.
|
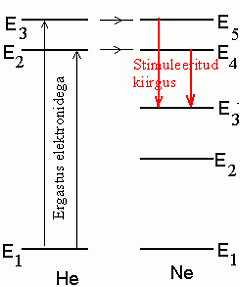
Heelium-neoonlaseri kiirgusmehhanism:
hõrendatud heeliumis tekitatud elektrilahendusel tekkiv kiirgus on resonantsis (sama sagedusega) kiirgustoru neooni energianivoodele E4 ja E5 üleminekuks vajaliku energiaga. Tekib pöördhõive, mis on eelduseks stimuleeritud kiirgusele.
|
|
Sellist valgusallikat nimetatakse
kvantgeneraatoriks; vastavalt genereeritavale lainepikkusele
nimetatakse neid inglisekeelsete lühenditega LASER (
Light Amplification by Stimulated Emission of Radiation,
valguse võimendi stimuleeritud kiirguse emisioonil) või
MASER (Microwave Amplification ..., mikrolaine võimendi
...).
Laseri näol on tehnikas nüüd siis olemas ka koherentse valguse
tekitamise vahend. See viis optika uuele tasemele, tänu
laseritele on tahkisefüüsikas ja spektraalanalüüsis võimalik
uurida üksikuid energianivoosid; laseri ülimalt kontsentreeritud
kiires leiavad aset seni saavutamatud protsessid, nagu
mitmefootoniline ergastus ja ionisatsioon. Laiatarbetehnikas on
tuntuim informatsiooni optiline salvestamine laserikiirguse abil
(nn. CD-tehnika) ning ruumiline fotograafia -
holograafia.
Laseriga teeme tutvust laboris. Huvilistele võin aga soovitada Henn
Käämbre "Laseriraamatut", üht parimat kodumaist pop-füüsika alast teost.
|
Stimuleeritud kiirgust iseloomustab võnkumiste korrastatus; kiir on monokromaatne, koherentne ja lineaarselt polariseeritud.
Küsimus: Mida need kolm omadust tähendavad?
|
![]() Aatomite karakteristlik kiirgus
Aatomite karakteristlik kiirgus
![]() Vesinikuaatom
Vesinikuaatom
![]() Üldistatud Balmeri valem
Üldistatud Balmeri valem
![]() Spektraalterm
Spektraalterm
![]() Aatomimudelid
Aatomimudelid
![]() Thomsoni aatomimudel
Thomsoni aatomimudel
![]() Rutherfordi katse ja planetaarne mudel
Rutherfordi katse ja planetaarne mudel
![]() Bohr'i teooria
Bohr'i teooria
![]() Naatriumi spekter
Naatriumi spekter
![]() Lainemehaanika
Lainemehaanika
![]() Lainehüpotees
Lainehüpotees
![]() Elektronide difraktsioon ja Davisson-Germeri katse
Elektronide difraktsioon ja Davisson-Germeri katse
![]() Lainefunktsioon ja Schrödingeri võrrand
Lainefunktsioon ja Schrödingeri võrrand
![]() Vaba osakese võrrand
Vaba osakese võrrand
![]() Võrrandi üldkuju
Võrrandi üldkuju
![]() Statsionaarse oleku võrrand
Statsionaarse oleku võrrand
![]() Lainemehaanika rakendusi
Lainemehaanika rakendusi
![]() Ühe-elektroni-üleminekud
Ühe-elektroni-üleminekud
![]() Kolm kvantarvu
Kolm kvantarvu
![]() Neljas kvantrv - spin
Neljas kvantrv - spin
![]() Määramatuse relatsioon
Määramatuse relatsioon
![]() Kvanditud faasiruum
Kvanditud faasiruum
![]() Pauli keeld ja kvantstatisrtika
Pauli keeld ja kvantstatisrtika
![]() Mendelejevi tabel
Mendelejevi tabel
![]() Pauli printsiibi põhjendus
Pauli printsiibi põhjendus
![]() Bosonid ja fermionid
Bosonid ja fermionid
![]() Elektronkihi energiatasemed
Elektronkihi energiatasemed
![]() Liitmine vektormeetodil
Liitmine vektormeetodil
![]() Termi tähis
Termi tähis
![]() Molekulide ja kristallide spektrid
Molekulide ja kristallide spektrid
![]() Kondenseerunud aine
Kondenseerunud aine
![]() Elektrijuhtivuse kvantteooria
Elektrijuhtivuse kvantteooria
![]() Kvantgeneraator
Kvantgeneraator
![]()