Loeng 16. Lained
Lainetus on üks liikumise liike: merepinnal liikuvaid
laineharju pidasid vana-aja inimesed omaette olenditeks -
need sündisid veest ja tuulest, läbisid oma rännuteel saari ja
sadamaid ning hääbusid lõpuks rannaliival.
Füüsikuid-filosoofe pani kõige rohkem imestama, et lainetega ei
kaasnenud liikumist selle tavapärases, aine (massi) edasikandumise
mõttes. Lainetaval veepinnal olev laev jäi paigale, kõikudes
lainetega samas rütmis. Mõnes mõttes käitusid lained liikuvate kehade
sarnaselt: kohates takistust, põrkab laine tagasi ja jätkab liikumist
vastassuunas; nurga all põrgates aga käitub nagu piljardikuul
(langemisnurk võrdub põrkenurgaga). Teiselt poolt, lainete
omavahelisel põrkel ei juhtu mitte kui midagi - pärast kohtumist
levivad lained edasi nii, nagu poleks teist lainet olemaski...
|
Lainetus (kulgev laine) erineb tavapärasest (kulg)liikumisest selle poolest, et temaga ei kaasne kehade ümberpaiknemine (kehade asukoha muutus).
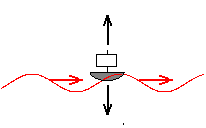
Laevuke lainetaval veepinnal.
|
|
Mõõtmistega saab näidata, et lainetava veepinna osakesed jäävad
"keskmiselt paigale", sooritades võnkeid tasakaaluasendi ümber.
Täpselt sama juhtub, kui raputada ühest otsast kinnitatud nööri.
Tekkiv võnkumine on korrastatud, st. iga osakese võnkefaas sõltub
lisaks ajale ka asukohast.
Laineid on erinevaid, uurimise
lihtsustamiseks saab neid mitmel viisil liigitada. Tuntuim liigitus
on rist- ja pikilained (viitab laine levikusuuna ja osakeste
võnkesuuna vahelisele nurgale), merelained kuuluvad
pinnalainete liiki, valgus ja röntgenikiired
elektromagnetlainete hulka. Kvant-teooria kasutab väljendeid
pilootlaine, tõenäosuslaine jms.; väga tuntud on häälelained.
Olemas on isegi selline kummaline objekt nagu seisevlaine.
Oma füüsikakursuses käsitleme kõige lihtsamat lainetuse liiki -
ühtlases keskkonnas levivaid elastsuslaineid. Leitud võrrandeid
kasutatakse kõigi teiste lainetuse liikide kirjeldamisel - täpselt
niisamuti, nagu harmoonilisi võnkeid keeruliste perioodiliste
liikumiste korral.
|
Lainetavas keskkonnas toimub osakeste korrastatud võnkumine.
Kui keskkonnaosakesed võnguvad risti laine liikumissuunaga, nimetatakse lainetust ristlaineks; kui samas sihis, siis pikilaineks.
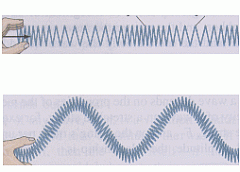
Pikilaine ja ristlaine
|
|
Elastsuslaine tekib keskkonnas, mille osakesed on püsivas
tasakaalus (aatomid kristallvõres, molekulid vedeliku pinnal) juhul,
kui mõne(de) osakes(t)e kohalt nihutamine rikub süsteemi
tasakaalu. Paigaltnihutatud osakese ja naaberosakeste vahel
tekivad sel juhul elastsusjõu tüüpi jõud, mis
- sunnivad paigaltnihutatud osakest pöörduma tagasi
tasakaaluasendisse;
- nihutavad paigalt naaberosakesed.
|
|
|
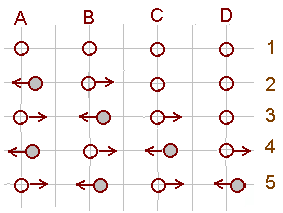
1 -- osakesed on tasakaalus
2 -- A nihutati paigast
3 -- AB vaheline tõukejõud on nihutanud B edasi
ja sundinud A liikuma tagasisuunas
4 -- B on nihkunud tagasi C ja A edasi,
5 -- A nihkus tagasi, B edasi, C tagasi, D edasi.
|
Võnkumiste levik osakeste vahelise jõu mõjul.
Nihkunud osakesed on tumedamad, noolekesed näitavad jõudusid.
| |
|
|
Pärast mõnesid võnkeid selline süsteem tasakaalustub, kuna
energiakaod on paratamatud. Iseasi on siis, kui võnkuv punkt
saab energiat juurde, näiteks harmoonilise jõu allikalt. Sellisel
juhul kandub võnkumine keskkonda ja tekib ruumis leviv lainetus.
Laineks nimetame keskkonna osakeste võnkumist, kus
võnkefaas sõltub allika kaugusest siinus (koosinus) funktsiooni
järgi.
|
|
|
Lainevõrrand. Seega kirjeldab lainet valem
kus 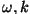 on konstandid, on konstandid, 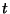 väljendab aega ja väljendab aega ja 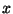 on
ruumikoordinaat. Suurust on
ruumikoordinaat. Suurust 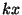 võib vaadelda kui kaugusest
sõltuvat algfaasi - või, teiste sõnadega, faasinihet, kus võib vaadelda kui kaugusest
sõltuvat algfaasi - või, teiste sõnadega, faasinihet, kus 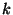 on
faasikonstant.
Samas faasis olevate keskkonnapunktide jaoks
kehtib nüüd on
faasikonstant.
Samas faasis olevate keskkonnapunktide jaoks
kehtib nüüd
|
Siinuslaines sõltub osakese võnkefaas lisaks ajale ka asukohast (ruumikoordinaatidest):
mistahes kahe osakese faasinihe on võrdeline nende osakeste vahelise kaugusega.
|
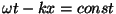 , ,
ehk
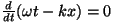 .
Võtnud tuletise, saame .
Võtnud tuletise, saame
|
X -telje suunas leviva laine võrrand on kahe muutuja - kauguse x ja aja t - harmooniline funktsioon.
|
|
Faasikiirus. Suurust
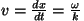 võime käsitleda
laine levimiskiirusena - niisuguse kiirusega liigub
(näiteks) lainehari veepinnal.
Muidugi liiguvad sama kiiresti ka
lainepõhjad ja üldse suvalise konstantse faasiga punktid.
Seetõttu nimetataksegi meie poolt leitud kiirust võime käsitleda
laine levimiskiirusena - niisuguse kiirusega liigub
(näiteks) lainehari veepinnal.
Muidugi liiguvad sama kiiresti ka
lainepõhjad ja üldse suvalise konstantse faasiga punktid.
Seetõttu nimetataksegi meie poolt leitud kiirust 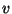 faasikiiruseks. faasikiiruseks.
|
Laineharja liikumiskiirust nimetame faasikiiruseks; sama kiirusega näivad liikuvat ka teised konstantse võnkefaasiga punktid.
|
Kui keskkond on homogeenne ja võnkumised toimuvad ainult ühe
sagedusega, on nii 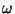 kui kui 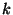 konstantsed kõigis punktides
ja igal ajal. Kirjutades konstantsed kõigis punktides
ja igal ajal. Kirjutades 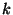 asemele asemele 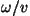 , saame
lainevõrrandi kujul: , saame
lainevõrrandi kujul:
Lainepikkus. Asendame nurksageduse 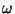 perioodi perioodi 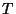 kaudu kaudu
(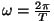 ) ja toome sisse uue suuruse, mis võrdub
kaugusega kahe laineharja vahel - lainepikkuse ) ja toome sisse uue suuruse, mis võrdub
kaugusega kahe laineharja vahel - lainepikkuse
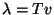 . (Kaugus kahe laineharja
vahel võrdub tee pikkusega, mille laine läbib sama ajaga, kui
osake teeb ühe täisvõnke.) . (Kaugus kahe laineharja
vahel võrdub tee pikkusega, mille laine läbib sama ajaga, kui
osake teeb ühe täisvõnke.)
|
Meelde jätta!
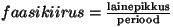
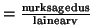
Tuletage nende dimensioonid!
|
|
Meie valem saab nüüd sümmeetrilise kuju:
Siit on hästi näha lainetusprotsessi korrastatus:
valides kindla ajmomendi 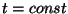 , saame valemi , saame valemi
kus osakeste
hälve on ruumikoordinaadi harmooniline funktsioon ning
faasinihe on määratud vaatlusmomendiga.
Analoogiliselt saame
suvalises keskkonna punktis meile hästi tuntud harmoonilise
võnkumise
|
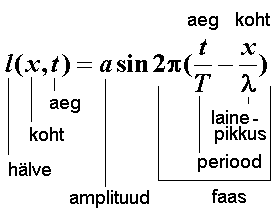
X-telje suunas leviva tasalaine võrrand perioodi T ja lainepikkuse 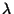 kaudu. kaudu.
|
|
kus hälve sõltub ajast ning algfaas vaadeldava punkti asukohast.
Lainevõrrand lausa nõuab aja ja ruumi samaväärsust. Just siit
viib tee relatiivsusteooriasse, aga ka kvantmehaanikasse. Kõik
oleneb sellest, kuidas saadud valemit tõlgendada. Saadud on
valem aga puhtempiiriliselt, looduslikku lainetust jälgides.
Tasalaine ja lainearv. Senitoodud valemid kehtivad 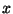 -telje
suunas leviva tasalaine kohta. -telje
suunas leviva tasalaine kohta.
|
Tasalaine, mille samafaasipindadeks on lõpmatu ulatusega tasandid, on arvutusi lihtsustav idealisatsioon.
|
|
Tasalaineks nimetame lainet,
mille samafaasipinnad on tasandid.
Loomulikult on selline
lõpmatute tasapinnaliste "harjadega" laine idealisatsioon.
Reaalsed lained on kas sfäärilised või väga keeruka kujuga.
Tasalaine valemit on lihtne üldistada suvalises suunas levivale
lainele. Lähtepunktist 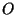 kaugusel kaugusel 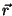 asuva punkti
faasinihke võime kirjutada asuva punkti
faasinihke võime kirjutada
kus 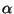 on nurk laine levimissuuna on nurk laine levimissuuna 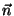 ja meie poolt
valitud punkti kohavektori ja meie poolt
valitud punkti kohavektori 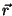 vahel. vahel.
Lainevõrrandiks saame
Et
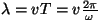 , siis , siis
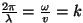 ning me võime
defineerida lainearvu ning me võime
defineerida lainearvu 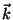 kui vektori, mille suund
ühtib laine levimissuunaga. kui vektori, mille suund
ühtib laine levimissuunaga.
Suunas 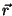 leviva
tasalaine võrrand avaldub seega kujul: leviva
tasalaine võrrand avaldub seega kujul:
|
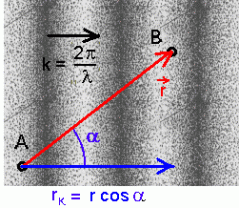
Tasalaine vektoresitus.
Korrutis 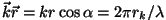 näitab faasi, st. mitu täislainet mahub punktide A ja B vahele. näitab faasi, st. mitu täislainet mahub punktide A ja B vahele.
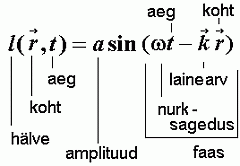
Ruumis leviva tasalaine võrrand nurksageduse 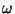 ja lainearvu
ja lainearvu 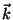 kaudu.
kaudu.
|
|
Laine energia. Konstantse amplituudiga lainetusest
haaratud ühtlase keskkonna koguenergia võrdub kõigi võnkuvate
osakeste energiate summaga. Et ühe võnkuva osakese energia avaldub
kujul
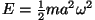 , siis tuleb kõigi ruumalas , siis tuleb kõigi ruumalas 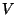 asuvate osakeste koguenergia just nii palju suurem, kuivõrd on selles
ruumalas olevate osakeste kogumass
asuvate osakeste koguenergia just nii palju suurem, kuivõrd on selles
ruumalas olevate osakeste kogumass 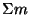 suurem ühe osakese massist: suurem ühe osakese massist:
kus 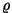 on aine tihedus. Võime arvutada ka energiatiheduse
laines, jagades koguenergia koguruumalaga: on aine tihedus. Võime arvutada ka energiatiheduse
laines, jagades koguenergia koguruumalaga:
Energiavoog laines. Et lainetus levib, kaasneb tema
liikumisega ka energia levik. Analoogselt vee vooluhulgale läbi
vooluga risti oleva pinna
võime defineerida laine energiavoo tiheduse
Energiavoo läbi suvalise pinna saame nüüd leida integraaliga
|
Lainetuse poolt edasi kantavat energiat kirjeldab energiavoo tiheduse vektor, mis on
võrdeline keskkonna tiheduse ja
laine levimiskiirusega ning
osakeste võnkeamplituudi ja
-sageduse ruutudega.
Vektori suund ühtib laine levikusuunaga.
|
|
Küsimus: Kõik kolm vektorit - lainearv, laine kiirus ja energiavoo tihedus - on samasuunalised, seega erinevad vaid skalaarse kordaja võrra. Kas oskate leida need kordajad?
Keralaine. Lainefüüsika rakendustes lähtutakse tavaliselt
punktikujulisest laineallikast (lühemalt: punktallikast).
Sellise allika ümber levivate lainete samafaasipinnad pole tasase,
vaid sfäärilise kujuga, mistõttu vastavat lainet nimetatakse
keralaineks.
Kuna punktallikas, mille võnkeamplituud
ajas ei muutu, kiirgab võrdsetes ajavahemikes lainena ruumi
konstantse energiahulga, ei saa selline laine olla konstantse
amplituudiga. Punkti ümber leviva keralaine
summaarne energiavoog jääb küll kõigil kaugustel samaks, see-eest
aga kahaneb energiavoo tihedus vastavalt kerapinna 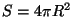 suurenemisele. Kaugusel
suurenemisele. Kaugusel 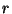 on energiavoo tihedus järelikult on energiavoo tihedus järelikult 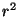 korda väiksem:
korda väiksem:
|
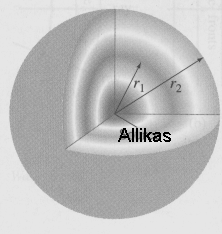
Keralaine punktikujulise laineallika ümber.
|
Et kõik lainet iseloomustavad suurused peale amplituudi on
konstandid, peab keralaine valem olema:
- muidugi juhul, kui laineallikas (punktallikas!) asub koordinaatide alguspunktis.
|
Keralaine amplituud väheneb võrdeliselt allika kaugusega.
|
|
Laine diferentsiaalvõrrand. Kuna harmoonilised võnked
olid kindlat tüüpi diferentsiaalvõrrandi lahendiks, võime küsida,
millise võrrandi lahendiks on laine.
Võtame lainevõrrandist
osatuletised koordinaatide järgi ja liidame kokku. Et
siis
|
NB! Siintoodu ei ole laine diferentsiaalvõrrandi koostamine füüsikalises mõttes, vaid eelnevalt olemas oleva lahendi - tasalaine võrrandi - diferentseerimine.
|
Analoogiliselt saame
Pärast liitmist saame
ehk
kus
on Laplace'i operaator (vt. vektoranalüüs!) ja 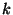 lainearvu
vektori lainearvu
vektori 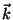 moodul. moodul.
|
Meelde jätta!
Tähis 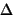 ei märgi siin suuruse l muutu, vaid tähistab Laplace'i diferentsiaaloperaatorit.
ei märgi siin suuruse l muutu, vaid tähistab Laplace'i diferentsiaaloperaatorit.
|
|
Võrreldes saadut lainevõrrandi teist järku tuletisega aja järgi
näeme, et
ehk
mis ongi laine diferentsiaalvõrrand.
|
Laplace'i operaator on matemaatiline teisenduseeskiri, mis seab skalaarsele väljale l (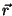 )
vastavusse tema teist järku tuletise ruumikoordinaatide järgi. )
vastavusse tema teist järku tuletise ruumikoordinaatide järgi.
Kui see tuletis on võrdeline sama välja ajalise tuletisega, tekib lainevõrrand.
|
|
Mida arvata? Saadud võrrand sisaldab märksa rohkem, kui temalt
oodati. Vaadake: ta seob ruumilist tuletist
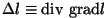 ajalise tuletisega ajalise tuletisega 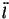 , kusjuures kordajaks on
laine levimiskiiruse ruut , kusjuures kordajaks on
laine levimiskiiruse ruut
Tühjas ruumis leviva elektromagnetlaine korral on selleks kiiruseks valguse kiirus
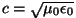 ja tagajärjeks nn. Lorentz'i
teisendus - otsetee relatiivsusteooriasse. ja tagajärjeks nn. Lorentz'i
teisendus - otsetee relatiivsusteooriasse.
Elastsuslaine kiirus. Senises jutus on faasikiirus
määramata - me saime ta vabalt valitud lainearvu 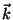 ja
keskkonnaosakeste omavõnkesageduse ja
keskkonnaosakeste omavõnkesageduse 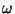 kaudu. Reaalsetes
(elastsetes) keskkondades on põhisuuruseks just laine kiirus;
lainepikkus aga sõltub sundiva jõu (võngete allika) sagedusest. kaudu. Reaalsetes
(elastsetes) keskkondades on põhisuuruseks just laine kiirus;
lainepikkus aga sõltub sundiva jõu (võngete allika) sagedusest.
|
|
|
Laine põhiparameeter on sagedus; keskkonna omadused
määravad lainete levikukiiruse ning alles nende kahe parameetri
kaudu saab leida lainepikkuse.
Elastsete keskkondade jaoks on laine levimiskiirus (heli kiirus)
määratud tihedushäirituse (lainefrondi, st. "esimese laine")
liikumiskiirusega.
Kui hakkame liigutama joonisel kujutatud
torus liikuvat kolbi, ei hakka liikuma kogu kolvi ees olev
vedelik (gaas, tahke aine) korraga, vaid elastsuse tõttu
jääb enamik ainest paigale, nihkub vaid kolvi lähedal olev osa.
Taskaaluseaduse järgi peab rõhk torus tasakaalustuma; see aga võtab
aega - häiritus levib kolvilt ruumi lõpliku kiirusega.
See ongi frondi kiirus, millega hakkab torus levima laine ja seda
saab kõige lihtsamini arvutada impulsi jäävuse seadusest:
|
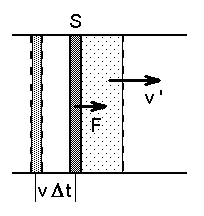
Elastsuslaine tekkimine liikuva kolvi ees.
|
Torus, kus jõud avaldub rõhkude vahena
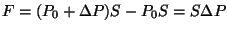 ,
võime selle kirjutada kujul: ,
võime selle kirjutada kujul:
(sulgudes olev avaldis võrdub liikuma hakanud ainehulga
massiga).
Kui jagada võrdust 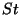 -ga, saame -ga, saame
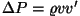 . .
|

Sama asi praktikas: hääleleinete tekitamine valjuhääldaja võnkuva membraani abil.
|
|
Nüüd on aeg sisse tuua elastsusjõud. Vedelikes ja gaasides on rõhumisjõud - järelikult ka rõhk - võrdeline suhtelise deformatsiooniga. Võrdeteguriks on nn. ruumelastsusmoodul 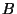 . Seega: . Seega:
Paneme nüüd sellesse võrrandisse 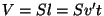 ning ning
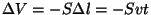 (miinus, kuna ruumala vähenes); saades (miinus, kuna ruumala vähenes); saades
kust saame laine(frondi) liikumiskiiruseks
|
|
|
Saadud valem, nagu muide kõik lainete ja võnkumistega seotud
valemid, kehtib vaid väikeste häirituste korral. Valem on
universaalne - käsiraamatutest võime leida terve paketi
analoogilisi valemeid:
|
Elastsuslaine (ka häälelaine) levimiskiiruse ruut on alati võrdeline keskkonna elastsusmooduliga ning pöördvõrdeline tihedusega.
|
|
Tavalises häälelaines (suhteliselt suured sagedused ja väike
amplituud) saame 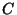 avaldada adiabaadi võrrandist avaldada adiabaadi võrrandist
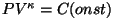 : :
Adiabaatilise laine kiiruseks ideaalses gaasis saame vastavalt
olekuvõrrandile
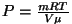 , ,
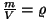 : :
Nägime, et elastsuslaine levimiskiirus aines sõltub ainult aine
omadustest, mitte aga võnkumiste sagedusest. Seega pole ka
lainepikkus mitte niivõrd lainet ennast kuivõrd laine ja
keskkonna vastasmõju kirjeldav suurus.
Laineprotsessi kirjeldab sagedus; laine levikukiirus ja
selle kaudu ka lainepikkus ning lainearv sõltuvad keskkonna
omadustest.
Elastsuslainete levikukiirust antud aines
nimetatakse helikiiruseks.
Näeme, et heli kiirus on võrdeline ruutjuurega
elastsustegurist ning pöördvõrdeline ruutjuurega tihedusest.
Mida raskem on aine, seda väiksem on heli kiirus. Tasub meeles pidada.
|
|
Elektromagnetlaine. Lainevõrrand võib välja ilmuda
sootuks ootamatult. Kui minna 13. loengus saadud Maxwelli võrrandites üle sama tüüpi muutujatele E ja H, saame:
Kui nüüd võtta esimesest võrrandist veel kord rootor, saame:
Asendades viimases liikmes
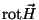 teisest võrrandist, teisest võrrandist,
ning teades (matemaatika!),et
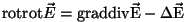 ja arvestades, et laengute puudumisel on ja arvestades, et laengute puudumisel on
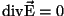 , saame lõpuks , saame lõpuks
|
See siin on vektoranalüüs. Ärge kurvastage, kui midagi aru ei saa. Kui vaja, õpite ära - asi polegi nii keeruline.
|
mis on puhtakujuline lainevõrrand vektorvälja 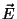 , seega
elektrivälja jaoks. , seega
elektrivälja jaoks.
Kui alustada
teisest võrrandist ja teha sama manipulatsiooni esimese
võrrandi abil, saame analoogilise lainevõrrandi
magnetvälja jaoks:
Need kaks võrrandit on paaris, nagu sukk ja saabas: ei saa me
"elektrilainet" magnetvälja abita ega "magnetlainet"
elektriväljata. Nii neid kokku nimetataksegi
elektromagnetlaine, aga veel sagedamini
elektromagnetvälja võrrandeiks.
|
|
|
Seega järeldub Maxwelli
võrrandeist matemaatiliselt keskkonnas kiirusega
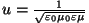 leviva
laine olemasolu. leviva
laine olemasolu.
Küllap Maxwell alguses imestas, kui elektromagnetismi rehkendustest lainevõrrand välja tuli. Aga ega imestamiseks
pikalt aega ei jäänud: lainete "eetrisse saatmine" avatud
võnkeringist oli niivõrd lihtne eksperiment, et Hertz'i
sädeinduktorit ja Popovi "äikesemärkijat" ei tulnud kaua oodata.
Elektromagnetlaine kujutab endast harmoonilise võnkumise
seaduse järgi muutuvat elektri- ja magnetvälja kombinatsiooni,
kus võnked toimuvad samas faasis (võrrandeis märgid samad).
|
Elektromagnetlainete teooria on aluseks nii sidetehnikale kui valguse laineteooriale.
|
|
Poynting'i vektor. Meie pilt kipub vägisi keeruliseks
minema: kaks ajas harmooniliselt muutuvat ning samal ajal lainena
ruumis levivat vektorvälja, mida omavahel seob keeruline teist
järku diferentsiaalvõrrandite süsteem. Vaja oleks lihtsat pilti,
mis hästi meelde jääb ning lainete põhivahekordi piisavalt
täpselt kirjeldab.
Tuleb välja, et kõike seda saab teha,
defineerides elektromagnetlaine energiavoo tiheduse valemiga:
Sellest, et vektorid on samas faasis, järeldub korrutis.
Sellest, et risti - vektorkorrutis. Märgid Maxwelli võrrandite
ajatuletiste ees määravad kolmiku orientatsiooni levikusuuna
suhtes.
Kõik ühe valemiga. See ongi Poynting'i vektor.
Energiatihedus ise võrdub elektri-
ja magnetvälja energiatiheduste summaga:
|
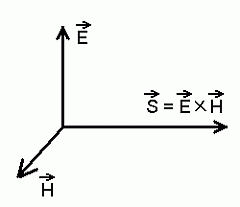
Poyntingi vektorkolmik.
|
|
Kui soovime leida energiavoogu läbi mingi pinna,
kasutame ülalpool leitud energiavoo pindintegraali:
kus 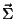 tähistab pindala, mida läbivat energiavoogu me
arvutame. tähistab pindala, mida läbivat energiavoogu me
arvutame.
Küsimus: Miks tähistasime siin pindala 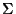 , mitte , mitte
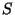 -ga? -ga?
|
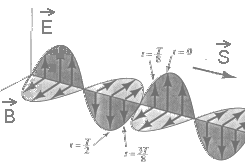
Elektromagnetlaine tavakujutus:
laine levikusuunaga ristsihis võnkuvad elektri- ja magnetvälja vektorid. Pange tähele: võnkumised on samas faasis ja teineteisega risti.
|
|
Doppleri efekt. Kogu senine matemaatika eeldab nii
laineallika, vastuvõtja kui keskkonna paigalseisu. Tegelikkuses
võivad kõik omavahel liikuda, mis mõjutab nii lainete kui neid
kirjeldavate valemite kuju ja omadusi.
Häälelainete kohta on teada, et läheneva allika (näiteks auto)
poolt tekitatav heli (mootorimürin) tundub toonilt kõrgem, kui
kaugeneva oma. Eriti selgelt on tooni muutus kuuldav auto
möödumisel. Et heli kõrgus peegeldab võngete sagedust, peab
viimane sõltuma allika liikumisest vastuvõtja suhtes.
Oletame, et laineallikas (võnkuv keha, ostsillaator) läheneb
meile kiirusega 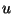 . Sel juhul on lainevõrrandis . Sel juhul on lainevõrrandis
|
Lainete sageduse muutumist laineallika liikumisel nimetatakse Doppleri efektiks.
|
olev suurus 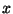 (allika kaugus) sõltuv ajast. Ühtlase liikumise
korral (allika kaugus) sõltuv ajast. Ühtlase liikumise
korral 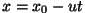 ja lainevõrrandi faasiosa ja lainevõrrandi faasiosa
kus
on uus, esialgsest suurem sagedus, mis hästi sobib praktikast
tuntud "kõrgema tooniga".
|
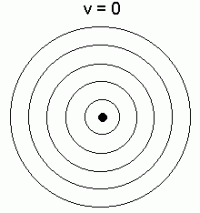
Paigalseis: ringlained punktallika ümber.
|
|
Toodud näites liikus allikas vastvõtja poole.
Matemaatiliselt annaks sama tulemuse ka vastuvõtja liikumine
laineallika poole, st. lainele vastu. Juhul, kui laineallikas
eemaldub vaatlejast, tuleb valemis märk vastupidine - sagedus
väheneb.
Saadud valemi tuletas Christian Doppler 1842. a., mille auks
nähtust
laine sageduse muutust allika-vastuvõtja omavahelise
liikumise tõttu - nimetataksegi Doppleri efektiks.
Valem töötab ka vektorkujul, st kui allikas liigub
laine levimissuunaga suvalise nurga all. Faasiliikme ruumiline
(vektor)komponent tuleb siis:
|
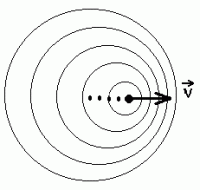
Doppleri efekt - ringlained liikuva punktallika korral.
|
|
millest lähtudes saame uue sageduse
kus 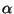 on nurk liikumissuuna ja laine levikusuuna vahel
ning on nurk liikumissuuna ja laine levikusuuna vahel
ning 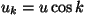 kiirusvektori kiirusvektori 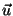 projektsioon laine
levimissuunale.
Valemi selline kirjutusviis kontrollib ka
parandi märki:
läheneva allika korral
( projektsioon laine
levimissuunale.
Valemi selline kirjutusviis kontrollib ka
parandi märki:
läheneva allika korral
(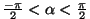 ) on ) on 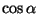 positiivne (sagedus
suureneb),
kaugeneva allika korral ( positiivne (sagedus
suureneb),
kaugeneva allika korral (
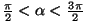 ) on ) on 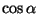 negatiivne (sagedus
väheneb). negatiivne (sagedus
väheneb).
|
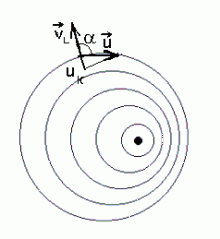
Nii kujuneb nurk lainevektori ja liikumissuuna vahel.
|
|
Mis juhtub, kui liigub vastuvõtja? Loogiline oleks kasutada sama
valemit, muutes parandusliikme märki. Tegelikult seda ei tehta:
lainete sagedust on oluline teada mitte kiirgaja, vaid
vastuvõtja seisukohalt. Seepärast loetakse lainevõrrandit
tavaliselt vastuvõtjaga seotud taustsüsteemis. Kui mingil
põhjusel on vaja teistsugust lähenemist, tuleb valemid viia
probleemiga vastavusse. Seda saab teha tavalise
koordinaatteisendusega (Galilei teisendus).
Kas liikumine keskkonna suhtes siis Doppleri efekti ei mõjuta?
Oleme harjunud laineid kirjeldama lainepikkuse abil ja see
sõltub tõepoolest keskkonna liikumisest. Joonisel on kujutatud
voolava vee pinnal levivate lainete kuju - laineid tekitab
veevoolu suhtes paigal seisev allikas.
Näeme, et kui enne olid laineharjad ringikujulised,
siis nüüd sõltub lainepikkus vee liikumisest,
olles suurem seal, kus laine ja vesi liiguvad ühes suunas ning
lühem vastassuunas. Et veeosakeste võnkesagedus on mõlemal juhul
sama, on lainepikkus
pildi vasakus servas väiksem, paremas servas aga suurem.
|
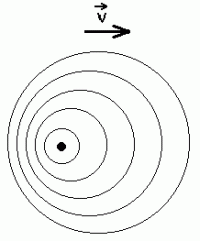
Ringlained voolava vee pinnal. Lainepikkused on küll erinevad, aga voolu suunas liitub voolu kiirus laine kiirusele, mistõttu paigalseisva vastuvõtja jaoks jääb võnkesagedus
samaks.
Aga vastuvoolu?
|
|
Muidugi mõjutab keskkonna liikumine ka laine levimise
kiirust. Jooniselt näeme, et pärivoolu saadetud signaal jõuab
adressaadini kiiremini, kui vastuvoolu sama kaugel oleva
vastuvõtja poole saadetu. Ja veel üks oluline asi: lainefrondi
kõverus, mis määrab (kera)laine amplituudi, on allavoolu
samadel kaugustel regulaarselt väiksem kui vastuvoolu. Seega
nõrgeneb vastuvoolu leviv laine kiiremini ja allatuult karjuda
tasub küll.
Superpositsiooniprintsiip. Samas keskkonnas võib asuda ja
võnkumisi tekitada ükskõik kui palju laineallikaid. Kõik need
võnked levivad keskkonda üheaegselt, mistõttu üks ja seesama
osake võtab osa paljudest võnkumistest. Klassikalise füüsika
seisukohalt on need võnkumised sõltumatud, mistõttu ka
kõik lained levivad keskkonnas nii, nagu poleks teisi laineid
olemas.
Seda eeldust, mis makrofüüsikas on katseandmetega heas
kooskõlas, nimetatakse superpositsiooniprintsiibiks. Printsiip
lubab laineid liita, lähtudes üksiklainete parameetreist.
Kvantteoorias, kus lainel on ka osakese omadused, tuleb lainete
liitmisel arvestada ka osakeste statistikalisi parameetreid
(kvantarve), mistõttu superpositsiooniprintsiip ei kehti.
|
Lainete sõltumatusest järeldub superpositsiooniprintsiip: et leida paljude lainete taktis võnkuva osakese liikumist, tuleb liita kõigi lainete poolt esile kutsutud võnkumised.
|
|
Matemaatiliselt eeldab superpositsiooniprintsiip nagu kogu
lainevõrrandki võngete väikest amplituuti lainepikkusega
võrreldes. Kui võngete ulatus läheb suureks, pole lained enam
sõltumatud. Aga siis ei kehti ka teised elastsuslaine valemid.
Huvitaval kombel on matemaatiline lainevõrrand, kord juba
(tegelikkuse lähendina, kuna sisaldab vaid Maclaurin'i rea kaht esimest liiget)
kirja pandud, immuunne kogu "klassikalise" füüsika aksiomaatika
suhtes.
Lainete liitmine. Alustame jällegi lihtsaimast
juhtumist, kus liituvate lainete sagedused on võrdsed. Et lained
levivad ühes ja samas keskkonnas, on sama ka
levimiskiirus ning seega ka lainearv. Erinevaiks jäävad
amplituudid ja loomulikult kaugused laineallikast.
Liitlaine võrrandi saame, kui liidame keskkonna mingi punkti
hälbed tasakaaluasendist (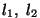 ) mingil ajahetkel ) mingil ajahetkel 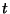 . .
Suurusi 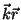 vaatleme kui algfaase ning kasutades
liitvõnkumiste amplituudide reeglit, saame vastuvõtja
poolt registreeritavaks võnkeamplituudiks vaatleme kui algfaase ning kasutades
liitvõnkumiste amplituudide reeglit, saame vastuvõtja
poolt registreeritavaks võnkeamplituudiks
Kui tegemist on punktallikate poolt tekitatavate
keralainetega, saab valemis olevale faasitegurile saab anda
lihtsama kuju. Sel juhul langeb lainevektori 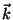 siht ühte
kohavektorite siht ühte
kohavektorite
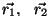 suundadega ning
skalaarkorrutised saab asendada lihtkorrutistega: suundadega ning
skalaarkorrutised saab asendada lihtkorrutistega:
|
Ringlainete liitumine.
Suundades, kus kohtuvad laineharjad, on võnkumise amplituud maksimaalne.
|
|
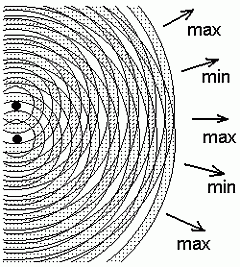
Interferentsivalemid. Siit on juba lihtne saada tingimused maksimumide ja miinimumide
jaoks:
Maksimum:
Miinimum:
Neid reegleid tuntakse interferentsivalemite nime all. Suurust, mille võrra erinevad samasse punkti saabuvate lainete poolt läbitud teepikkused, nimetatakse lainete käiguvaheks .
|
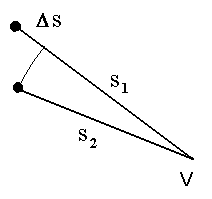
Käiguvahe.
|
|
Nagu võnkumistegi korral, vastab maksimumile laine, mille
amplituud on võrdne liidetavate lainete amplituudide summaga,
miinimumile aga amplituudide vahe. Ülejäänud punktides on
laine amplituud nende kahe äärmuse vahel.
Tekkivat
laineamplituudide ruumjaotust nimetatakse
interferentsipildiks, täpsem väljend oleks küll "amplituudide
väli".
Huvitav on seejuures asjaolu, et välja pilt näib olevat
ajas muutumatu - statsionaarne. Üksiku laine korral näeme
visuaalselt laine liikumist, võnkumine aga "jääb varju";
liitlaine korral on vastupidi - me ei märkagi laineharjade
liikumist, selle asemel näeme erineva amplituudiga
võnkuvate kehade hulka.
Visake üheaegselt vette kaks kivi. Algul näete levivaid
ringlaineid, mõne aja pärast need kohtuvad. Jälgige
kohtumispiirkonda: seal muutub veepind "muhklikuks" ning
liikumise illusioon kaob.
Interferentspilti nimetatakse sageli ka seisevlaineks.
Õpikutest võib jääda mulje, nagu tekiks seisevlaine vaid
vastassuunas levivate lainete liitumisel . See pole päris õige.
Mõeldud on seal ühemõõtmelist juhtu (piki pillikeelt või orelivilet kulgevad lained) - siis on tõesti ainus
võimalik interferents seotud vastassuunas levivate lainetega.
|
Sama kiirusega levivate lainete liitumisel tekkivat võnkumiste ruumjaotust nimetatakse seisevlaineks.
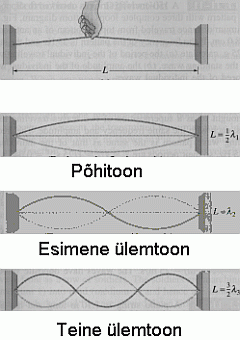
Seisevlaine näide: võnkuv pillikeel.
|
|
Lainepakett, soliton, rühmakiirus. Liikuma hakkab
interferentsipilt juhul, kui liituvate lainete sagedused on
erinevad. Nüüd on lugu nii, et amplituudivalemis lisandub
faasitegurisse ka ajast sõltuv liige, mis sarnaneb
liitvõnkumistest tuntud tuiklemise valemiga.
Faasitegurisse lisandub liige
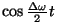 ,
millele vastavalt laineformalismile tuleks lisada ,
millele vastavalt laineformalismile tuleks lisada
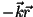 . .
Kui lained levivad samas suunas, asendab tuiklemistest
tuntud perioodilist maksimumi ruumis laine levimiskiirusega
liikuv lainepakett - jada suurema amplituudiga võnkumisi.
Juhul, kui lained ei levi samas suunas, muutub pildi
matemaatiline kirjeldamine keeruliseks. Sõltuvalt
lähtetingimustest võib lainepakett seista paigal, liikuda koos
ühe või teise lainega või koguni mingis kolmandas suunas.
Sellist hulkuvat lainet nimetatakse solitoniks ja tema
kohta on kirjutatud üsna palju raamatuid.
Üheks lihtsamaks(?)
juhtumiks on, kui lainete levimiskiirus sõltub nende sagedusest.
Seda juhtub keskkondades, mis koosnevad omavõnkesagedusi
omavatest osakestest - nn ostsillaatoritest.
Sellisel
juhul kulgeb soliton laine levimiskiirusest (faasikiirusest)
erineva kiirusega, mida nimetatakse rühmakiiruseks.
|
Eri sagedustega ning erineva kiirusega levivate lainete liitumisel võib kujuneda lainepakett, mille liikumiskiirus ei tarvitse kokku langeda faasikiirusega.
Lainete liitumisega seotud probleeme käsitleme pikemalt laineoptika loengus.
|
![]() Ristlaine ja pikilaine
Ristlaine ja pikilaine
![]() Elastsuslaine
Elastsuslaine
![]() Lainevõrrand
Lainevõrrand
![]() Faasikiirus
Faasikiirus
![]() Lainepikkus
Lainepikkus
![]() Tasalaine ja lainearv
Tasalaine ja lainearv
![]() Laine energia
Laine energia
![]() Energiavoog laines
Energiavoog laines
![]() Keralaine
Keralaine
![]() Laine diferentsiaalvõrrand
Laine diferentsiaalvõrrand
![]() Laplace'i operaator
Laplace'i operaator
![]() Elastsuslaine kiirus
Elastsuslaine kiirus
![]() Elektromagnetlaine
Elektromagnetlaine
![]() Poynting'i vektor
Poynting'i vektor
![]() Doppleri efekt
Doppleri efekt
![]() Superpositsiooniprintsiip
Superpositsiooniprintsiip
![]() Lainete liitmine
Lainete liitmine
![]() Interferentsivalemid
Interferentsivalemid
![]() Lainepakett, soliton, rühmakiirus
Lainepakett, soliton, rühmakiirus
![]()