SISUKORDA

Elektromagnetism Elektromagnetismi kolm põhikatset Amper'i seadus Vasaku käe reegel Vektorkorrutis Lorenz'i jõud Sirgvoolu väli Bio'-Savart'-Laplace' seadus Parema käe reegel Kahe sirgvoolu vastasmõju Ampri definitsioon Tööjuhtme liikumisel magnetväljas Elektromagnetiline induktsioon Induktsiooni elektromotoorjõud Induktsiooni definitsioon Eneseinduktsioon Maxwelli võrrandid

 

Loeng 13. Elektromagnetism.

Elektrivoolu magnetilistest omadustest oli juttu üle-eelmises loengus, seoses H. Ørsted (Oersted, eestipäraselt Örsted) juhusliku avastusega, mis sai tänapäeva magnetismiteooria aluseks. Örsted märkas, et vooluga juhtme lähedusse sattunud magnetnõel pöördus alati juhtmega risti olevasse suunda.

Elektromagnetism uurib elektrivooluga kaasnevaid magnetnähtusi.

Niisiis - magnetvälja jõujooned vooluga juhtme ümber kujutavad suletud kõveraid. Et sellest välja nimetatakse matemaatikas pöörisväljaks, mainisime loengus 11. Kui päris täpne olla, siis loodigi pöörisväljade matemaatiline teooria just magnetvälja kirjeldamiseks.

Kuna magnetlaenguid pole olemas, ei saa me magnetvälja jaoks kasutada nn. "punktlaengu lähendit". Magnetväli ei ole kunagi tsentraalsümmeetriline. Magnetlaengu puudumine ei lase meil niisama lihtsalt defineerida isegi mitte väljatugevust, rääkimata potentsiaalist.

Ainus, mida saame rehkendada, on magnetpulgale mõjuv jõumoment. Pulka ennast saaks ehk kirjeldada kaksiklaenguna - dipoolina. Elektrostaatikas defineeritakse dipoolmoment kui "varda" otstes asuva laengu korrutis varda pikkusega. Magnetiga on asi keerulisem - õnneks tuleb siin appi elektromagnetism.

Kui tekib vajadus magnet- ja elektrivälja võrrelda, kasutatakse tavaliselt homogeense välja lähendit. Homogeenseks nimetatakse välja, mille väljatugevuse vektor on kõigis väljapunktides ühesugune. Loomulikult saab selline tingimus kehtida vaid ligikaudu ja üsna piiratud ruumiosas. Homogeenne elektriväli tekib kahe ühtlaselt laetud plaadi vahel (näiteks plaatkondensaatoris); homogeense magnetvälja saame, kui keerame magnetpulga rõngasse ning jätame pooluste vahele kitsa pilu.

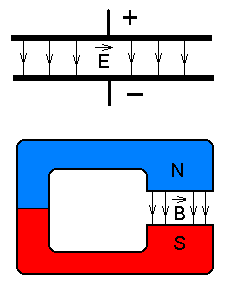
Homogeenne elektri- ja magnetväli.

Selles loengus toodud valemid kehtivad homogeenses magnetväljas

On ka teisi võimalusi, aga neist hiljem.

 

Elektromagnetismi kolm põhikatset.

Esimene katse: magnetnõel pöördub vooluga juhtme suhtes risti.	Teine katse: Magnetväljas asuv juhe hakkab liikuma, niipea kui teda läbib vool.	Kolmas katse: Mähises tekib elektrivool niipea, kui teda mõjutatakse magnetiga.

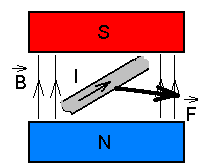
Ühest katsest oli juba juttu - see oli Örsted'i katse magnetnõelaga. Samal 1820. aastal tegi Andre Ampere katse, milles näitas, et magnetväljas asuvale vooluga juhtmele mõjub jõud, mis on võrdeline voolutugevusega. Katsete seeria tulemusena sai Ampere empiirilise valemi

 

$$F=IlB\sin\alpha,$$

kus $I$ on voolutugevus, $l$ juhtme pikkus, $B$ magnetvälja iseloomustav suurus, nn. magnetiline induktsioon ja $\alpha$ nurk magnetvälja suuna ja juhtme vahel. Kirjutades juhtme pikkuse vektorina $\vec l$ nii, et vektori suund ühtib voolu suunaga juhtmes, võime Ampere'i seaduse kirjutada vektorkujul:

Elektromagnetism on põhimõtteliselt kolmemõõtmeline: kõik tema valemid pannakse kirja kas rootori või vektorkorrutisega.

$$\vec F=I(\vec l\times\vec B)$$

Magnetilise induktsiooni ühikuks SI süsteemis on tesla (T); ta defineeritakse vooluga raamile magnetväljas mõjuva jõumomendi kaudu. Tesla dimensiooniks saame Ampere'i seadusest

$$[B]={{[F]}\over{[l][I]}}={N\over{A\cdot m}}={{kg}\over{s^2A}}=T$$

Ja nüüd siis verbaalsed definitsioonid:
 

Ampere'i seadus: Vooluga juhtmele magnetväljas mõjuv jõud on võrdeline voolutugevuse, juhtme pikkuse ja magnetilise induktsiooniga ning magnetvälja ja voolu suundade vahelise nurga siinusega. Jõud on risti nii juhtme kui magnetväljaga, tema suuna määrab vasaku käe reegel.

Tesla on sellise välja magnetiline induktsioon, kus vooluga raamile, mille pindala on 1 $m^2$, mõjub maksimaalne jõumoment 1 Nm, kui raamis on vool 1 A.

  Vasaku käe reegel:

Kui panna vasak käsi nii, et magnetvälja jõujooned on suunatud peopessa ning sõrmed näitavad voolu suunda, siis näitab välja sirutatud pöial juhtmele mõjuva jõu suunda.

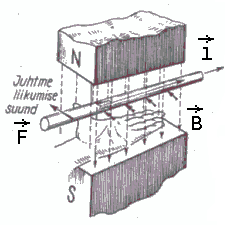
Vasaku käe reegel

  Matemaatiline vahepala: kuidas portreteerida vektorkorrutist

Elektromagnetism on põhimõtteliselt kolmemõõtmeline: enamus tema valemitest sisaldavad vektorkorrutist. Tuletame meelde definitsiooni:

Kahe vektori vektorkorrutiseks on vektor, mille mooduliks on teguritele ehitatud rööpküliku pindala ning mis on risti mõlema vektoriga. Vektorid $\vec a$, $\vec b$ ja $\vec a\times\vec b$ moodustavad parempoolse kolmiku.

Niisiis: korrutiseks olev vektor on risti tasandiga, mille moodustavad kaks korrutatavat vektorit. Need kaks (nimetatakse teguriteks) võivad olla teineteise suhtes mistahes nurga all, korrutis on aga igal juhul nende tasandiga risti.

See annabki meile võimaluse vektorkorrutise portreteerimiseks. Paneme tegurid joonise tasandisse ning märgime kolmanda vektori (korrutise) ringikesega. See ringike, mille juurde kirjutatakse vastava vektori märk, näitabki, et tegu on joonise tasandiga ristseisus oleva vektoriga.

Aga vektoril on ka suund, ta võib olla suunatud joonise suhtes nii ette- kui tahapoole. Et kaht suunda eristada, joonistatakse ringikese sisse kas punkt või rist. Punkt tähendab, et vektor on suunatud vaatleja poole (vaatleja näeb läheneva noole tippu), rist aga seda, et vektor on suunatud joonise taha (vaatleja näeb minema lendava noole sabasulgi).

Vektorkorrutis koordinaatkujul:

$$\vec a \times \vec b$$

$$=(a_yb_z-a_zb_y)\vec i$$

$$+(a_zb_x-a_xb_z)\vec j$$

$$+(a_xb_y-a_yb_x)\vec j$$

ja determinandina:

$$\vec a \times \vec b= \left\vert\matrix{ \vec i & \vec j & ... ...\cr a_x & a_y & a_z \cr b_x & b_y & b_z \cr} \right\vert$$

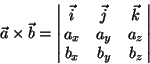
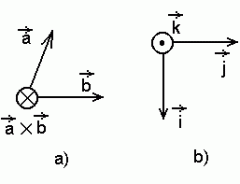
Noolereegel: a) vektorkorrutis;
b) ortonormaalne reeper kui "parempoolne kolmik".

Nimetame seda võtet "noolereegliks" ja kasutame oma joonistel homogeense magnetvälja kujutamiseks. Juhtmete, juhtmekeerdude ja laetud osakeste liikumist ning neile nõjuvaid jõude on nii väga mugav kujutada.

Küsimus: Korrutustehte kirjeldamisel rääkisime kahest tegurist, mitte "korrutatavast" ja "korrutajast". Seda selle pärast, et tava-arvude matemaatikas oli korrutustehe kommutatiivne (korrutis ei sõltunud tegurite järjekorrast). Aga kuidas on lood vektorkorrutisega?

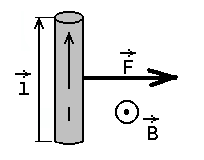
Ampere'i seadus noolereegliga antud magnetväljas. Kontrollige vasaku käe reeglit!

  Lorentz'i jõud. Et elektrivool koosneb liikuvatest laengutest, tähendab vooluga juhtmele mõjuv jõud tegelikult liikuvatele laengutele mõjuvat jõudu. Selle jõu saab välja arvutada, lähtudes voolutiheduse definitsioonidest:

$$\vec j={j\over{\vec S}}=nq\vec v~~\Rightarrow~~I=jS=nqvS.$$

Pannes selle Ampere'i jõu valemisse, saame

$$F=IlB\sin\alpha=nqvSlB\sin\alpha.$$

Et juhtme ruumala on $V=Sl$, siis on temas $N=nV=nSl$ liikuvat laetud osakest. Kui soovime leida ühele osakesele mõjuvat jõudu, tuleb juhtmele mõjuv jõud F jagada laetud osakeste arvuga N.

$$f={F\over N}={F\over{nSl}}=qvB\sin\alpha,$$

ehk vektorkujul

$$\vec f=q(\vec v\times \vec B),$$

mis ongi Lorentz'i jõud.

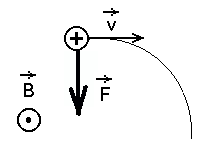
Lorentzi jõud ja osakese trajektoor noolereegliga antud väljas.

Nagu vektorkorrutisest järeldub, on temagi risti kiirusega. Seega ei muuda ta osakese liikumise kiirust, vaid ainult liikumise suunda.

Küsimus: Milline on magnetväljas liikuva laetud osakese trajektoor?

Nagu näeme, mõjub magnetväli ainult laetud osakestele. Et sama kehtib ka elektrivälja kohta, peab elektri- ja magnetnähtuste vahel olema seos. Tänapäeva füüsika on seisukohal, et tegemist on ühe ja sama nähtuse - elektromagnetismi - erinevate avaldumisvormidega. Seejuures on suhteliselt sõltumatud vaid ajas muutumatu tugevusega nn. staatilised väljad, muutuv elektromagnetväli sisaldab alati nii elektri- kui ka magnetkomponenti.

Lihtne reegel meelespidamiseks: staatilist elektrivälja tekitavad nii paigalseisvad kui liikuvad laengud; staatilist magnetvälja aga ainult ühtlase kiirusega liikuvad elektrilaengud - alalisvool. Juhtivuse teooriates me eitasime ühtlaselt voolavat elektrit (lisaks triivkiirusele oli alati olemas ka soojusliikumise kaootiliselt muutuv kiirus). Et soojusliikumises olevate laetud osakeste poolt tekitatud väljad annavad summana nulli, võib neid magnetismi uurimisel ignoreerida. Iseasi on muidugi nn. molekulaarsed voolud, mis avalduvad aine magnetiliste omaduste kaudu (vaata 11. loengut).

 
Sirgvoolu väli. Biot'-Savart'-Laplace'i seadus. Kirjeldades Örstedi katset, märkisime, et vooluga juhtme lähedale pandud magnetnõel pöördus alati juhtmega risti. Seejuures jäi aga mainimata, et nõel asetus ristsuunda ka tema pöörlemistsentrit juhtmega ühendava sirge suhtes. Viimane aga tähendab,et magnetvälja tugevus on juhtmest võrdsetel kaugustel ühesugune.

Seega peavad magnetvälja jõujooned:

• olema ringikujulised,
  
• nende tsentrid peavad asuma juhtmel ning
  
• nende tasandid peavad olema juhtmega risti.

Et valemit lõplikult kirja panna, tuleb veel katseliselt kindlaks teha magnetvälja sõltuvus juhtme kaugusest ja voolutugevusest.

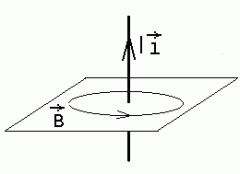
Sirgvool, teda ümbritseva magnetvälja ringjooneline jõujoon ning selle tasand.

Sirgvoolu magnetväli ja laetud varda elektriväli kahanevad mõlemad võrdeliselt kaugusega, kuid on erineva suunaga.

Vastava katseseeria viisid esimesena läbi Jean Biot ja Felix Savart 1820. a., kasutades välja allikana sirgjuhet. Nad tegid kindlaks, et väljatugevus on võrdeline voolu tugevusega juhtmes ning pöördvõrdeline juhtme kaugusega. Et saadud valem $B=b{I\over B}$ on sarnane ühtlaselt laetud lõpmata pika sirge elektrivälja valemiga $E=2k{{\eta}\over r}$, formuleeris Pierre Laplace diferentsiaalvalemi

$$dB=b{{Idl\sin\alpha}\over{r^2}},$$

mille integreerimisel tuleb välja ülaltoodud empiiriline valem.

Aga ettevaatust - sarnasus on näiline! Kui teeme "noolediagrammi" juhtmega (laetud vardaga) ristuvas tasandis, on kohe näha, et elektriväli lähtub vardast (jõujooned on radiaalsed), magnetväli aga ümbritseb varrast (jõujooned on kontsentriliste ringide kujulised.

Et erinevust matemaatiliselt väljendada, tuleb valem kirja panna vektorkujul:

$$\vec{dB}=b{I\over{r^3}}(\vec{dl}\times\vec r)$$

Kuna Laplace kasutas Gaussi CGSM-süsteemi, omas võrdetegur b väärtust $b=2/c$ ($c$ on, nagu ikka, valguse kiirus). SI-süsteemis kirjutatakse teda kujul ${{\mu_0}\over{4\pi}}$, kus $\mu_0 =4\pi\cdot 10^{-7}$ H/m on magnetiline konstant (nn. vaakuumi magnetiline läbitavus).

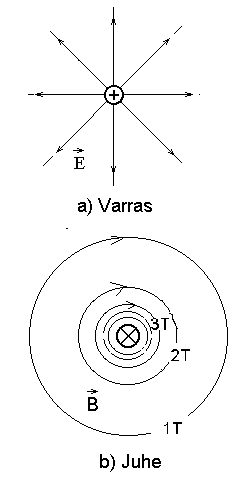
Sirgvoolu magnetvälja ja laetud varda elektrivälja jõujooned noolediagrammil.

Ja lõplik valem:

$$\vec{dB}={{\mu_0}\over 4\pi}{I\over{r^3}}(\vec{dl}\times\vec r)$$

  Biot'-Savart'-Laplace'i seadus:

Vooluelemendi poolt tekitatava magnetvälja magnetiline induktsioon on võrdeline voolutugevusega ning pöördvõrdeline vooluelemendi kauguse ruuduga. Välja suund on risti nii vooluelemendi kui ka väljapunkti vooluelemendiga ühendava sirgega; suuna määrab (parema käe) kruvi reegel.

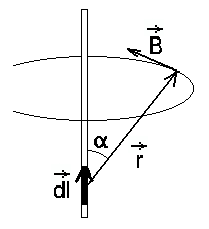
Vooluelemendi magnetväli ja Biot'-Savart'-Laplace'i valem.

  Parema käe ehk kruvi reegel:

Kui (parempoolne) kruvi panna liikuma piki vooluga juhet nii, et kruvi pea pöörlemine ühtib magnetilise induktsiooni vektori suunaga, siis kruvi ise liigub voolu kulgemise suunas.

Seda, et ülaltoodud diferentsiaalseos on samaväärne B-S valemiga sirgvoolu kohta, saab näidata lihtsa integreerimisega.

Võtame sirgjuhtmel tükikese pikkusega $dl$, mille kohta kehtib BSL valem. Et saada kogu juhtme välja, peame integreerima analoogiliselt "laetud sirge" elektriväljaga. Jooniselt näeme, et

$$r={b\over{\sin\alpha}}~~{\rm ja}~~dl={{rd\alpha}\over{\sin \alpha}}= {{bd\alpha}\over{\sin^2\alpha}}.$$

Pannes need BSL valemisse, saame:

$$dB={{\mu_0}\over{4\pi}}{{Ibd\alpha\sin\alpha \sin^2\alpha}\over{b^2\sin^2\alpha}}={{\mu_0I}\over{4\pi b}}\sin\alpha d\alpha.$$

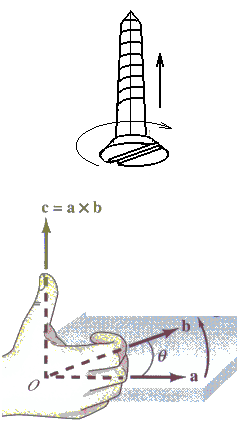
Kruvireegel ja selle lääne analoog - parema käe reegel.

Integreerides seda üle $\alpha$ nullist $\pi$-ni, saamegi

$$B={{\mu_0I}\over{2\pi b}}$$

Analoogilise integraaliga võime leida ka ringvoolu (vooluga juhtme, mis on ringjoone kujuline = juhtmekeerd!) välja. Siin on asi isegi lihtsam. Ringjoone tsentri jaoks on

$r=R=const$, $dl=Rd\varphi$, $\alpha=\pi/2$

ning

$$B=\int^{2\pi}_0{{\mu_0}\over{4\pi}}{{IRd\alpha }\over {R^2}}={{\mu_0I}\over{2R}}.$$

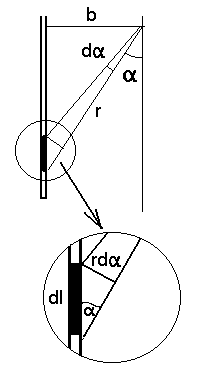
Integraal piki juhet: sirgvool.

Pisut keerulisema matemaatikaga saame

$$B={{\mu_0}\over 2}{{R^2I}\over{{(R^2+x^2)}^{3/2}}},$$

punkti jaoks, mis asub ringvoolu teljel kaugusel $x$ tsentrist.

$N$ juhtmekeerust koosneva pooli korral tuleb $B$ loomulikult $N$ korda suurem.

  Kahe sirgvoolu vastasmõju. Ampri definitsioon. See, et elektrivool samaaegselt nii tekitab magnetvälja kui on ka vastasmõjus välise magnetväljaga, võimaldab anda voolutugevuse ühikule niisuguse määratluse, mis ei sõltu magnetvälja ühikutest.

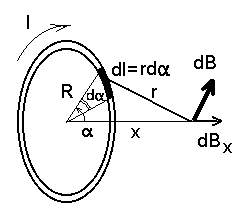
Integraal piki juhet: ringvool.

Vaatleme kaht paralleelset sirgjuhet, mis asuvad teineteisest kaugusel $b$ ja milles voolab ühesugune elektrivool tugevusega $I$. Üks neist (pole tähtis, kumb!) tekitab teise juhtme asukohas magnetvälja

$$B={{\mu_0I}\over{2\pi b}},$$

mis Ampere'i seaduse kohaselt mõjutab seal asuvat juhet jõuga

$$F=IlB(\sin\alpha =1)={{\mu_0}\over{2\pi}}{{I^2l}\over b}.$$

Nagu näeme, pole valemis peale $I$ ühtki tundmatu dimensiooniga suurust. Võttes $l$ ja $b$ väärtusteks ühiku (SI süsteemis meeter), saame ühikulise voolutugevuse korral

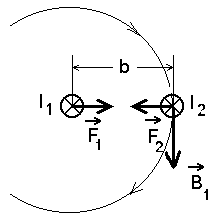
Sirgvoolude vaheline jõud noolediagrammil.

$$F={{\mu_0}\over{2\pi}}=2\cdot 10^{-7}.$$

  Ampri definitsioon SI-süsteemis:

Üks amper on selline voolutugevus, mis kulgedes piki kaht
• lõpmata pikka
  
• väikese ristlõikega
  
• vaakumis
  
• teineteisest 1 m kaugusel paiknevat
  
• paralleelset sirgjuhti,

  kutsub nende vahel esile jõu $2\cdot 10^{-7}$ njuutonit meetri kohta.

Toodud definitsiooni võiks nimetada ka ampri etalooniks. Ta määrab võrdeteguri ${{\mu_0}\over{2\pi}}$ väärtuse juhul, kui voolutugevust mõõdetakse amprites, jõudu njuutonites ja kaugusi meetrites.

  Töö juhtme liikumisel magnetväljas. Oletame, et risti magnetväljaga asuv juhe saab vabalt liikuda. Temale mõjuva jõu (Ampere'i seadus!) mõjul liikudes teeb juhe tööd

$$A=Fs=IBls=IB\Delta S=I\Delta\Phi,$$

kus $\Delta S$ on juhtme liikumisel tema poolt kaetud pindala ning $\Delta\Phi$ sellele pinnale vastav magnetilise induktsiooni vektori voog. Et vool saab eksisteerida ainult vooluringi kujul, võime suurust $\Delta S$ ette kujutada kui vooluga kontuuri poolt piiratud pindala muutu. Kasutanud vektorvälja voo matemaatilist definitsiooni ($\Phi=\int_{\Sigma}\vec B\vec{dS}=\int_{\Sigma}\vec B\vec n dS$), "peitsime" oma valemis vektorite taha kõik juhtme liikumise ja orientatsiooniga seotud nurgad.

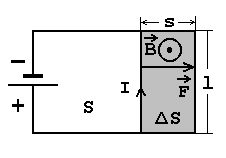
Vooluga juhtme liikumisel magnetväljas tehtud töö on võrdeline kontuuri pindala muutusega.

Seega on juhtme liikumisel magnetväljas tehtud töö võrdeline voolutugevusega juhtmes ning vooluringi läbiva magnetvoo muutusega. Lihtsaimal juhul (vooluga tasapinnaline raam) võime vektorvõrrandi "lahti kirjutada" järgnevalt:

$$A=I\Delta(\Phi=Bls\cos\alpha),$$

kus $\alpha$ on nurk raami tasandile tõmmatud normaali ja magnetilise induktsiooni vektori $\vec B$ suuna vahel.

Märgime, et Ampere'i seaduses olnud nurk $\alpha$ vastas nurgale juhtme ja vektori $\vec B$ vahel. Praegu pole matemaatiliselt enam oluline, kas magnetvoo $\Phi$ muutus on tingitud kontuuri pindala ($ls$), magnetvälja enda ($\vec B$) või koguni nurga $\alpha$ muutumisest.

Et magnetilise induktsiooni vektori voog (lühemalt magnetvoog) on sageli kasutatav suurus, on tema ühikul

$$[\Phi]=[B]\cdot[S]=T\cdot m^2=Wb$$

omaette nimi - veeber.

Võib küsida, millise energia arvel seda tööd tehakse. Et jõud mõjub ainult vooluga juhtmele, oleks loogiline väita, et voolu (vooluallika energia) arvel. See töö lisandub Joule-Lenz'i seadusega $A=I^2R\Delta t$ määratud (soojuslikule?) tööle, andes kogu tehtud töö magnetilise töö ning juhtmes eralduva soojuse summana:

$$A=I\Delta\Phi+I^2R\Delta t$$

Voolu poolt magnetvälja abiga tehtud töö on jõumasinate (elektrimootorite) aluseks. Endastmõistetavalt on konstruktorid huvitatud, et magnetiline töö oleks võimalikult suur ning soojusena kaotsi läinud energiahulk võimalikult väike.

  Induktsiooni elektromotoorjõud. Mis juhtub aga siis, kui vooluringis puudub vooluallikas (ja järelikult ka vool), aga teda läbiv magnetvoog sellegipoolest muutub? Matemaatiliselt peab siis $I=0$-st järelduma $A=I\Delta\phi=0.$
Aga võib arutleda ka teistmoodi: et kogu vooluringis tehtav töö on võrdne elektromotoorjõu ja voolutugevuse korrutisega, siis

$$I{\cal E}\Delta t=A=I\Delta\Phi,$$

millest

Elektromagnetiliseks induktsiooniks nimetatakse elektromotoorjõu (st. elektrivälja!) teket muutuva magnetvälja mõjul.

NB! Mitte segi ajada magnetilise induktsiooniga, mis on magnetvälja tugevust kirjeldav suurus.

$${\cal E}={{\Delta\Phi}\over {\Delta t}}.$$

Matemaatiliselt jällegi korrektne. Aga mida see füüsikaliselt tähendab?

Võiksime väita, et juhtme liikumise tõttu magnetväljas või mingil muul põhjusel kontuuri läbiva magnetvoo muutumine kutsub esile elektromotoorjõu, mille suurus on võrdeline magnetvoo muutumise kiirusega. Katse näitab, et selline efekt on tõesti olemas. Mis on aga põhjus?

Põhjuseks on Lorentz'i jõud. Kui liigutame magnetväljas juhti, milles on vabu laenguid, sunnib see laetud osakesi liikuma vastavalt juhtme liikumise suunale. Kui juht (juhe) on seejuures liikumissuunaga risti, kogunevad positiivsed laengud juhtme ühte, negatiivsed aga teise otsa. Juhtmes tekib elekriväli, mille suund on vastupidine Lorentzi jõu suunale.

Induktsiooni elektromotoorjõu seletamine Lorentz'i jõuga:
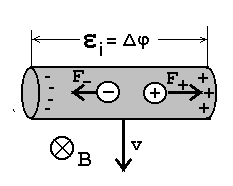
koos juhtmega liikuma sunnitud laetud osakesed liiguvad Lorentzi jõu mõjul juhi otstesse, tekitades nii potentsiaalide vahe.

Kui

$$\vec F_e=q\vec E=-q(\vec v \times\vec B)=-\vec F_L,$$

siis laengute liikumine lõpeb - laetud osakesele mõjuvad jõud on tasakaalus.

Võib üelda ka nii: juhtme otste vahel on tekkinud potentsiaalide vahe

$$\Delta\varphi=\vec E\vec l=(\vec v\times\vec B)\vec l={d\over{dt}}(\vec s\times\vec B)\vec l.$$

Leitud valemile saab anda üsnagi universaalse kuju. Selleks teisendame tuletise märgi taha jäävat korrutist:

$$\Delta\varphi =-{d\over{dt}}(\vec s\times\vec l)\vec B=-{d\over{dt}}\vec S_{s\times l}\vec B=-{{d\Phi}\over{dt}}$$

Ampere'i seaduse seletus:
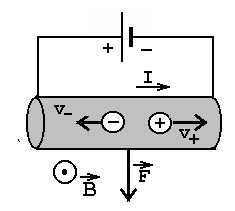
juhtmes liikuvatele laengutele mõjuv Lorentzi jõud pöörab need vasakule, sundides nii liikuma kogu juhtme.

See potentsiaalide vahe tekib mitteelektriliste jõudude mõjul ja teda võib käsitleda kui elektromotoorjõudu. Nii teda nimetataksegi - induduktsiooni elektromotoorjõud.

Kokku:
  Elektromagnetiliseks induktsiooniks nimetame nähtust, kus magnetvoo muutumine kutsub kinnises kontuuris esile elektromotoorjõu, mis on võrdeline magnetvoo kahanemise kiirusega:

$${\cal E}_{ind}=-{{d\Phi}\over{dt}}.$$

Nagu töö valemis, pole ka siin oluline, mis põhjusel magnetvoog muutub. Ühtviisi hästi mõjub nii kontuuri pindala muutus (juhtme liikumine), kontuuri tasandi pöörlemine kui ka magnetilise induktsiooni $\vec B$, st magnetvälja enda muutus. Miinusmärk tähendab seda, et induktsiooni elektromotoorjõu poolt esile kutsutav vool takistab magnetvoo muutumist - tema magnetväli on suunatud esialgsega samas suunas, kui magnetvoog väheneb ja vastassuunas, kui magnetvoog suureneb.

  Eneseinduktsioon. Et iga vooluga juhet ümbritseb magnetväli, mille tugevus on võrdeline voolutugevusega juhtmes, kutsub voolutugevuse muutumine juhtmes alati esile teda ümbritseva magnetvälja muutuse.

Viimane tähendab, et voolutugevuse muutumine juhtmes tekitab sellessamas juhtmes induktsiooni elektromotoorjõu. Seda nähtust nimetataksegi eneseinduktsiooniks. Kuna magnetväli on võrdeline voolutugevusega, siis on ka magnetvoo muutumise kiirus võrdeline voolutugevuse muutumise kiirusega - siit saame nn Lenz'i reegli :

Eneseinduktsiooniks nimetatakse juhis voolutugevuse muutusel tekkivat elektromotoorjõudu, mille põhjustab vooluga kaasneva magnetvälja muutumine.

Induktsiooni elektromotoorjõud on võrdeline voolutugevuse muutumise kiirusega juhtmes ning suunatud nii, et tema mõju takistaks voolutugevuse muutumist juhis.

Lenz'i reegel valemiga:

$${\cal E}_i=-L{{dI}\over{dt}}$$

Võrdle valemeid: Inertsijõud kiirendusega

liikuvas süsteemis on

Võrdetegur $L$ sõltub juhi kujust ning keskkonna magnetilistest omadustest. Teda nimetatakse antud juhi induktiivsuseks.

Induktiivsuse ühikuks on henri (H)

Üks henri on sellise juhi induktiivsus, kus voolutugevuse muutus üks amper sekundi kohta kutsub esile eneseinduktsiooni elektromotoorjõu üks volt.

$$[L]={{[{\cal E}][t]}\over{[I]}}={{Vs}\over A}=H$$

Elektromagnetilise induktsiooni nähtus on sarnane inertsinähtusega mehaanikas: ta takistab magnetvälja või voolutugevuse muutumist.

  Maxwelli võrrandid. Mäletatavasti tähendas elektromotoorjõud tööd, mida tegid mitteelektrilised (kõrval)jõud ühikulise laengu läbiviimisel kontuurist. Seda tööd võib kirja panna ringintegraalina - tsirkulatsioonina:

$${\cal E}_i=\oint\vec E\vec{ds}=-{{d\Phi}\over{dt}}=-{d\over{dt}}\int_S\vec B\vec{dS}.$$

Et diferentseerimine ja integreerimine toimuvad üle erinevate argumentide, võib nende järjekorda muuta. Kirjutame

$$\oint\vec E\vec{ds}=-\int_S\Bigl({{d\vec B}\over{dt}}\Bigr)\vec{dS}.$$

See ongi esimene "suur" Maxwelli võrrand - tavalises kõnepruugis Esimene Maxwelli võrrand integraalkujul. Verbaalselt oleks see järgmine:

"Sõrmusediagramm":
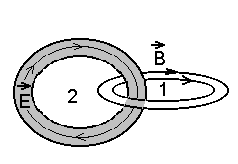
kui pöörisvälja B (sõrmus 1) voog läbi kujuteldava kontuuri (sõrmus 2) muutub, tekib selles pööriseline (suletud jõujoontega) väli E, mille tsirkulatsioon annab kontuuris tehtava töö.
Seda tööd väljendabki "suur Maxwelli võrrand".

Elektrivälja tugevuse tsirkulatsioon piki suletud kontuuri on võrdeline seda kontuuri läbiva magnetvoo muutumise kiirusega.

Teise analoogilise võrrandi mõtles Maxwell välja, lähtudes "sümmeetriakaalutlustest":

$$\oint \vec H\vec{ds}=\int_S\Bigl({{d\vec D}\over{dt}}\Bigr)\vec{dS}+\int_S\vec j\vec{dS};$$

voolu sisaldav liige tuleneb elektrilaengute olemasolust.

Kui nende kahe võrrandiga minna piirile (kontuur koondub punktiks), saame:

$$\hbox{rot}\vec E=-{{\partial\vec B}\over{\partial t}}$$

$$\hbox{rot}\vec H=\vec j+{{\partial\vec D}\over{\partial t}}$$

Siia lisanduvad veel allikfunktsiooni markeerivad võrrandid Gaussi teoreemist:

$$\hbox{div}\vec B=0$$

$$\hbox{div}\vec D=\varrho$$

Need neli võrrandit tuletas James Clerk Maxwell 1876.a. ja nad olid "esimene pääsuke" tänapäeva teoreetilises füüsikas. Nii et tasub meelde jätta.

Pealegi - neist tuleb veel juttu. Sest just neist neljast võrrandist sai alguse elektromagnetlainete teooria.

Vektorvälja tsirkulatsioon ja voog on väljateooria põhimõisted; tuntud USA füüsikapedagoog Robert Feynman on andnud neile hästi meelde jäävad sõnalised definitsioonid:

Voog = pindala korda väljavektori keskmine normaalisuunaline komponent

Tsirkulatsioon = kontuuri pikkus korda väljavektori keskmine puutujasuunaline komponent

Meelde võib ju jääda, aga kas aru ka saime?