SISUKORDA

Laineoptika Newtoni rõngad Fermat' printsiibi laineinterpretatsioon Young'i katse Fresnel'i katsed Koherentsete allikate mõiste Interferents tehnikas Samakalde interferents Samapaksuse interferents Valguse difraktsioon Fresnel'i tsoonid Huygens'i-Fresnel'i printsiip Cronu' spiraal Fraunhoferi difraktsioon Difraktsioonivõre Keralaine difraktsioon Tsooniplaat ja Fresnel'i läätsed Mikroskoobi ja teleskoobi piirlahutusvõime Difraktsioon ruumilistelt tõketelt Hologramm

Loeng 18. Laineoptika

Kui korpuskulaarhüpoteesil põhinev geomeetriline optika olnuks vigadeta, puuduks ka vajadus laineteooria(te) järele. Paraku nii see ei olnud: korpuskliteoorial oli olulisi puudusi.

Üht neist - valguskiirte sõltumatust - mainisime eelmises loengus. Mis mainimata jäi, oli see, et Huygensit ärgitas laineoptika loomisele nähtus, mida peeti (peetakse tänini!) üheks optika suuremaks mõistatuseks - valguse kaksikmurdumine.

Huygens lõi laineoptika eesmärgiga seletada valguse kaksikmurdumist: erinevas suunas levivate ristvõnkumiste levimiskiirused on erinevad.

Nähtuse avastas E. Bartholinus 1670. aastal.

Kui trükitekstile asetada islandi paost valmistatud läbipaistev plaat, paistab selle alla jääv tekst kahekordsena. Valguskiire jagunemist kaheks oleks korpusklitega kaunis raske seletada. Kui aga oletada, et valgus on (rist)lainetus, võib vabalt juhtuda, et aine elastsusmoodul on ühes suunas suurem kui teises. Erinev on sel juhul ka erinevates suundades võnkuvatele osakestele vastavate lainete kiirus ning sellest johtuvalt ka aine murdumisnäitaja.

Täpselt nii Huygens arutleski. Oletame, et sellisele ebatavalisele ainele langeb "tavaline" valgus - kindla suunaga ristvõnkumine.

Islandi pagu

Osakesed hakkavad võnkuma, kuid selle võnkumise ülekandumine järgmistele osakestele sõltub võnkesuunast: "pehmes sihis", kus elastsustegur väiksem, levib võnkumine väiksema kiirusega kui "jäigas sihis" toimuv võnkumine.

Kahele kiirusele vastab kaks murdumisnäitajat,

kahele murdumisnäitajale kaks kiirt,

kahele kiirele (geomeetrilise optika reeglite kohaselt!) aga kahekordne kujutis.

Paraku on see üksnes kaudne seletus. Laineteooria kriitiline eksperiment - experimentum crucis - on ikkagi interferents, lainete liitumine faasinihet arvestavalt. Kuni seda näidata ei õnnestunud, ei saanud laineteooriat usaldada.

 
Newtoni rõngad. Kontrollides lihvimisel oleva läätse kvaliteeti, avastas Newton läätse ja selle aluspinna kokkupuutepunkti ümbritsevate kontsentriliste rõngaste süsteemi.

Rõngaste olemasolu polnud korpuskulaarteoorias seletatav; seetõttu tuli Newton välja mõttega, et liikuvad korpusklid tekitavad keskkonnas (eetris) võnkumisi, mis omakorda mõjutavad keskkonna optilisi omadusi. Hinnates rõngaste läbimõõtude järgi läätse ja aluspinna vahelise seisevlaine pikkust, sai Newton üsna tänapäevase tulemuse - pool mikromeetrit.

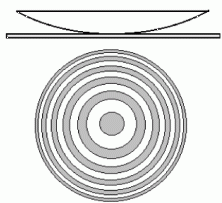
Newtoni rõngad.

Tasapinnalisele plaadile asetatud läätse all tekib kontsentriliste tumedate rõngaste süsteem.

Lähenemisviis meenutab mingil määral kvantmehaanika selgitustes esinevat nn. pilootlaine hüpoteesi. Sellest võib järeldada, et Newton siiski tunnistas võimalust, et valgusel on ka laineomadused. Tänapäeval nimetatakse sellist "kahesust" valguse dualismiks.

 
Fermat' printsiibi laineinterpretatsioon. Oma printsiipi sõnastades vältis Fermat viiteid valguse olemuse kohta, seega võime vabalt oletada, et ta kirjeldas sellega korpuskli trajektoori. Selgusetuks jääb, mis sunnib korpusklit "parimat trajektoori" valima.

Newtoni oletus kiiruse suurenemise kohta annab kvalitatiivselt õige pildi ainult üleminekul tihedamasse keskkonda - sisepeegeldust ning selle piirnurka ei saa kuidagi seletada kiiruse vähenemisega murdval pinnal.

Asi muutub, kui me valguskiirte või korpusklite voo asemel kujutleme murdvale pinnale langevat tasalainet.

Siis tähendab eri teid mööda tulevate kiirte hilinemine automaatselt faasi erinevust.

Kõige väiksem erinevus naaberkiirte vahel tuleb ekstreemumi (miinimumi) lähedal, kus teeloleku aeg muutub aeglasemalt. See, umbes poolemillimeetrilise laiusega ribale langev valgus moodustab suurema osa intensiivsusest punktis $B$.

Kõik ülejäänud kiired interfereeruvad paariti ning mingit olulist lisa intensiivsusesse ei anna.

Sama pilt tuleks ka peegeldumisel, aga tol pole mingeid eeliseid "põrkuvate korpusklitega" võrreldes. Seepärast loeme olulisemaks just ülaltoodud mõttekäiku.

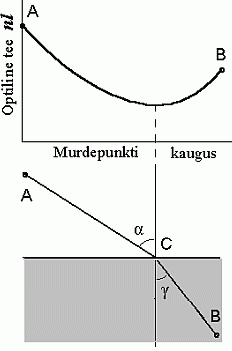
Fermat' printsiip:

optiline tee pikkus (valguse levimiseks punktist A punkti B kulunud aeg) sõltub tihedamasse keskkonda mineku kohast.

Fermat' printsiipi saab seletada erinevat teed pidi tulnud valguslainete vahelisest faasinihkest tingitud interferentsiga.

 
Young'i katse. Esimese korrektse interferentsikatse valguslainetega tegi Young 1802. a. Tal õnnestus praktikas rakendada Huygensi printsiipi - tekitada sama lainefrondi kahe punkti poolt kiiratavate sekundaarlainete vaadeldav interferents.

Young'i katseskeem on lihtne:

• päikesekiirte või mõne muu heleda valgusallika poolt valgustatud pilu $A$ taga asub piluga paralleelne läbipaistmatu ekraan, millesse on lõigatud piluga $A$ paralleelsete pilude paar $B$ ja $C$.
• Huygens'i printsiibi kohaselt levib pilu $A$ taga silindrilise frondiga sekundaarlaine, millest pilud $B$ ja $C$ "lõikavad välja" kaks sama faasiga allikat.
• Nende poolt kiiratavad lained interfereeruvad ekraanil $E$, andes lihtsalt arvutatava pildi, kus interferentsimaksimumid (heledad ribad) vahelduvad tumedate miinimumidega.

See "lihtne arvutus" on aga järgmine: leiame kõigepealt Pythagorase teoreemist kiirte pikkuste ruudud:

$$s_1^2=l^2+({d\over 2}+h)^2$$

ja

$$s_2^2=l^2+({d\over 2}-h)^2.$$

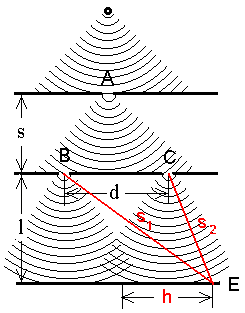
Young'i katse. Piludelt B ja C lähtunud (sekundaar)lained liituvad ekraanil E.
Tekib interferents - liitlaine amplituudi sõltuvus faasinihkest.

Lahutades esimesest võrdusest teise, saame

$$s_1^2-s_2^2=2hd,$$

millest saamegi teepikkuste vahe

$$s_1-s_2={{2hd}\over{s_1+s_2}}\approx{{2hd}\over{2l}}$$

(juhul, kui$l\gg d$).

Heledate ja tumedate ribade asukohad on nüüd määratud kiirte käiguvahega - teepikkuste vahe $s_1-s_2$ ning lainepikkuse $\lambda$ suhtega:

• maksimum, kui $\mid s_1-s_2\mid=n\lambda$

• miinimum, kui $\mid s_1-s_2\mid=(2n+1){\lambda\over 2}$

Oleks nagu lihtne katse, aga kui seda mujal proovima hakati, ei tulnud enamasti midagi välja. Tänapäeval teatakse, et katse õnnestumiseks peab olema täidetud tingimus:

pilud $A$, $B$ ja $C$ peavad paiknema nii, et

$$b\sin\omega\leq 0.25\lambda,$$

kus $b$ on pilu $A$ laius ja

$$\tan\omega ={d\over{2s}}$$

($s$ on esimese ekraani kaugus pilust $A$).

Youngi katse õnnestub ainult pilude kindla asendi ning laiuste korral.

Kui pilu laius on suurem, satub sellesse "mitu sekundaarallikat" ning juba piludel $B$ ja $C$ tekib interferents - see muudab meie valemid mittekehtivaks. Teiseks oluliseks puuduseks on nõrk valgustatus ekraanil $E$, kuna pilu $A$ on väga kitsas ning katsesse pääseb seetõttu vähe valgust.

Young seda ei teadnud, tema kaasaegsed ammugi mitte. Selles, et katse õnnestus, oli paras jagu õnnelikku juhust. Tekkinud poleemika kutsus esile suure hulga katsetajaid ning viis lõppkokkuvõttes laineteooria taassünnile.

 
Fresnel'i katsed. Kus päris teadus võimetu, löövad tihtipeale läbi profaanid. 1811. a. sattus E. Malus' loengule valguse polarisatsioonist teedevalitsuse insener Augustine Fresnel. Loomulikult oli temagi koolis õppinud "õiget" korpuskliteooriat; seda enam köitis noort uurijat lihtne võimalus seletada polarisatsiooni võnkumiste abil. Fresnel asus asja kallale, hea matemaatikuna õnnestus tal muu töö kõrvalt tuletada ülaltoodud interferentsivalemid (olid muidugi juba varem teada, aga mitte Fresnel'ile).

Fresneli tähtsamad ja rakenduslikumad tööd on seotud difraktsiooniga, aga alustas ta interferentsikatsetest. Kahe pilu asemel kasutas ta ühe valgusallika kahte optilist kujutist. Nii on näiteks kahe peegli või kahe prisma abil võimalik saada kaks samaväärset kiirtekimpu, mille heledus on tunduvalt suurem kui Young'i kitsastest piludest tulevatel kiirtel.

Veel näitas Fresnel, et interferentsipilt tuleb selgem ja teravam, kui kasutada ühevärvilist (monokromaatset) valgust. Maksimumide/miinimumide asukohti ekraanil saab arvutada Youngi katse valemitest, kui lugeda $l$ võrdseks valgusallikate kujutiste kaugusega ekraanist ning $d$ kujutiste omavahelise kaugusega.

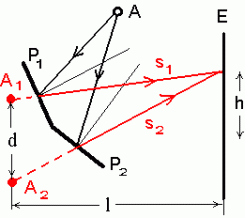
Fresnel'i kaksikpeegel.

Valgusallika A peegeldumisel kahelt väikese nurga all asuvalt peeglilt tekib kaks valguslainet, mis on samaväärsed "peegli taga" asuvatelt allikatelt tulevatega.

 
Koherentsete allikate mõiste. Miks siis ikkagi ei ole võimalik saada valguskiirte interferentsi sama lihtsalt, kui häälelainete korral?

Esimene põhjus on muidugi kaduvväike lainepikkus. Kui me liigume kahe valjuhääldiga ruumis, siis on miinimumide-maksimumide vahekaugus meetri suurusjärgus - see vastab häälelainete pikkusele sagedusel 330 Hz. Valguslainete korral on vastav arv $6\cdot 10^{-7}$ m (0.0006 mm), seda meie silm eraldada ei suuda.

Muidugi - kui asetada allikad lähestikku, suurendada ekraani kaugust ning kasutada kujutise vaatamiseks luupi, võime maksimumide vahelist kaugust märgatavalt suurendada. Interferentsi sellegipoolest ei teki.

Põhjus arvatakse olevat kiirgusallikate eripäras. Esiteks kiirgab valjuhääldi katkematut siinuslainet (mis vastab generaatoris tekitatavale vahelduvvoolule), valgus aga tekib (näit. hõõglambis) soojusliikumise poolt genereeritud juhuslike kiirgusimpulsside jadana. Iga sellise impulsi kestus on määratud põrgete kestuse ja atomaarsete võngete sumbuvuse kiirusega. Katseliselt on kindlaks tehtud, et üks aatom (molekul) kiirgab keskmiselt $10^{-8}$ sekundi vältel, saates (valguse kiirust vaakumis arvestades) välja umbes kolme meetri pikkuse siinuslaine. (See "lainejupp" sisaldab lühidusele vaatamata kuni miljardit võnget!)

Teiseks: häälelained on pikilained, valgus aga ristlainetus. Pole lootust, et omavahel nurga all olevate võnketasanditega ristlained interfereeruksid - parimal juhul saame mingi Lissajous' kujundi, see aga ei mõjuta mingil moel silmaga tajutava kiirguse intensiivsust.

Niisiis, "tavaliste" (on olemas ka ebatavalisi!) valgusallikate korral pole lootagi võnkumiste interferentsiks vajalikku korrastatust. Seda viimast nimetavad füüsikud koherentsuseks, mis sõna-sõnalt ladina keelest tõlgituna tähendab seostatust või kokkukuuluvust. Võnkumiste koherentsuse all mõistetakse faasivahe säilivust ajas ja ruumis; vajaduse korral eristatakse ruumilist ja ajalist koherentsust.

Koherentseteks nimetatakse (valgus)allikaid, mille poolt kiiratud (valgus)lainete faasinihe on kogu aeg ühesugune.

Ülaltoodu järgi peaks ajalise koherentsuse piiriks olema $10^{-8}$s ja ruumilisel koherentsusel 3 meetrit. Tegelikud arvud on väiksemad, kuna meie kolmemeetrised lainejadad paiknevad-levivad ruumis juhuslikult. Nii tuleb "garanteeritud koherentsus" välja umbes kümme korda väiksemate mastaapide korral; ühe meetri juures algab efekti märgatav nõrgenemine (pakettide otsad lähevad teineteisest mööda) ja kolme meetri lähedal pole koherentsusest enam jälgegi.

Tänapäeva tehnoloogia tunneb ka valgusallikaid, kus koherents säilub praktiliselt piiramatu aja jooksul. Need on kvantgeneraatorid - laserid. Nagu nimigi ütleb, põhineb nende töö kvantmehaanikal ja seetõttu käsitleme neid hiljem.

Tavalised valgusallikad pole koherentsed; kui soovime tekitada valguse interferentsi, peame kasutama sama allika kaht kujutist.

 

Interferents tehnikas. Mõnedel juhtudel tekivad koherentsed allikad iseenesest. Kui tingimused on soodsad, näeme siis vikerkaarevärvilisi ribasid või laike. Tuntuim interferentsi tekitaja on mingi suure murdumisnäitajaga aine õhuke kiht - siis tekib interferents kihi kahelt küljelt peegeldunud valguslainete vahel.

 

Samakalde interferents tekib, kui paralleelne kiirtekimp (päikesevalgus) langeb tasaparalleelsele plaadile (jääkiht veelombi pinnal). Siis näeme korraga kaht kiirt: ühte, mis peegeldub (jää)kihi ülemiselt ja teist, mis peegeldub alumiselt pinnalt. Kuna teise kiire tee on pikem, hilineb ta faasis

$$\Delta\varphi =2\pi{{s_1-s_2}\over \lambda}$$

võrra. Arvestades, et optiliselt tihedamas keskkonnas kasvab "optiline tee pikkus" $n$ korda ($n$ on murdumisnäitaja), saame käiguvaheks

$$\Delta=2AB-AD=2n{d\over{\cos\beta}}-2d\tan\beta\sin\alpha.$$

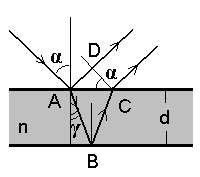
Samakalde interferents.

Tasaparalleelse kihi kahelt küljelt peegeldunud kiirte vahel tekib faasinihe, mis sõltub langemisnurgast.

Et murdumisseaduse järgi on $sin\alpha=n\sin\beta$, tuleb (pärast paari algebralist teisendust)

$$\Delta=2d\sqrt{n^2-\sin^2\alpha}.$$

Niisiis: kui $\Delta=n\lambda$, võimendavad kiired teineteist ning pind tundub heledana. Et $\Delta$ väärtus sõltub vaatenurgast (kiire kaldest) nimetataksegi nähtust samakalde interferentsiks. Nurgad, millele vastab maksimum, saame valemist $\Delta=k\lambda$, kus $k$ on täisarv. Seega

$$\Delta^2=k^2\lambda^2=4d^2(n^2-\sin^2\alpha),$$

ehk

$$\sin\alpha=\sqrt{n^2-{{k^2\lambda^2}\over{4d^2}}}.$$

Nii on näiteks peaks ühe millimeetri paksuse klaasplaadi korral olema 30-kraadise nurga all näha 4714. maksimum, 4715.maksimum aga asub 3.7 kaareminuti võrra madalamal. Kas proovime?

 

Samapaksuse interferents tekib juhul, kui vaatame muutuva paksusega kihti mingi kindla nurga all. Lähtevalemiks võib olla eelmise punkti (samakalde) valem, ainult et nüüd on muutujaks mitte $\alpha$, vaid $d$. Maksimume näeme nüüd vaadeldava kihi neis piirkondades, kus

$$\Delta=k\lambda=2d\sqrt{n^2-\sin^2\alpha}.$$

Siit tuleb õige lihtne tingimus -

$$d={{k\lambda}\over{2\sqrt{n^2-\sin^2\alpha}}}.$$

Samapaksusribasid oleme kõik näinud, vaadates veepinnal laialivalguvat õlikilet. Vikerkaarevärvilised laigud õli pinnal pole midagi muud, kui kohad, kus nähtavale värvile vastavas lainepikkuses on interferentsimaksimum. Ribade suhteliselt suur laius tuleneb asjaolust, et õlikile on väga õhuke - tema paksus on tõepoolest mikroni suurusjärgus. Seetõttu on ka paksuse kõikumised väikesed ja sama käiguvahe esineb suhteliselt suurtel pindadel.

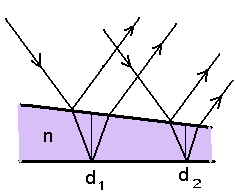
Samapaksuse interferents.

Ka ülalmainitud Newtoni rõngad on samapaksusribad. Läätse toetuspinnaga risti vaadates näeme korraga kahte kiirt - üht, mis peegeldub alusplaadilt, ja teist, mis peegeldub läätse alumiselt pinnalt. Õhukihi paksus sõltub tsentri kaugusest:

$d=R-\sqrt{R^2-r^2}$,

kus $R$ on läätse kõverusraadius ja $r$ kaugus tsentrist ehk miinimumi korral vastava Newtoni rõnga raadius.

Tingimus $2d=k\lambda$ lubab meil arvutada rõngaste raadiused läätse kõverusraadiuse funktsioonina:

$$r=\sqrt{R^2-(R-{{k\lambda}\over 2})^2}.$$

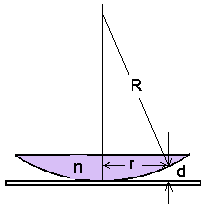
Newtoni rõngad kui samapaksusribad.

Tavaliselt kasutatakse küll lihtsamaid lähendvalemeid.

Valguse interferentsi kasutatakse optikatööstuses valgusfiltrite valmistamisel. Kui tavaline värvitud klaasist filter laseb valgust läbi küllalt suures lainepikkuste vahemikus, siis kattes klaasalust erineva murdumisnäitajaga ainete täpselt välja arvutatud kihtidega, võime saada filtri, mille läbilaskeriba on vaid mõne nanomeetri laiune.

Hoopis huvitava idee peale tulid fotoobjektiivide valmistajad. Kuna interferentsimiinimumi korral kilega kaetud klaas valgust tagasi ei peegelda, järeldasid nad, et "kadunud valgus" peab minema klaasi sisse. Selle tulemusena aga suureneb klaasi läbilaskvus ja objektiiv "näeb paremini". See, nn. selgendatud optika (e. sinine optika) on fotograafias, eriti aga binoklite juures, üsna levinud.

Ja veel üks interferentsi rakendus - kauguste mõõtmine interferomeetritega. Peegeldavate pindade korral on interferentsimaksimumide vahe pool lainepikkust ja see lubab mõõta pinna kaugust (või täpsust) vähem kui 10 nanomeetrise veaga.

 

Valguse difraktsioon. Valguse laineiseloom mõjutab ka valguskiire möödumist tõketest. Terav geomeetriline vari, nagu ta tuleneb korpuskulaarteooriast, osutub täpsemal vaatlemisel üsna detailirohkeks. Eriti torkab see silma väikeste esemete või avade korral, kus lainetele tüüpiline levimine tõkete taha on suhteliselt hästi jälgitav. Tavaliselt näeme nn. difraktsioonipildis vahelduvaid heledaid ja tumedaid ribasid (sirgjoonelise varju piiril) või siis kontsentrilisi rõngaid (väikese ava taga või väikese tõkke varju ümber). See, interferentsipildile tüüpiline efekt viiski Fresneli mõttele, et

difraktsioonipilt tekib lainefrondilt lähtuvate sekundaarlainete interferentsi tulemusena.

 

Fresnel'i tsoonid. Oli ta kuidas oli, igatahes tekkis Fresnelil geniaalne mõte jagada lainefront tsoonideks. Et kõik frondi punktid on samas faasis, pole vaja arvestada laine poolt allikast frondini läbitud teed. Jääb ainult tee frondilt kuni vaatluspunktini.

Kui nüüd ühendada geomeetriliselt need lainefrondi punktid, mille kaugus vaatluspunktist on $n\lambda$, saame pinna, mille kõik punktid üksteise kiirgust võimendavad. Summaarne kiirgus on loomulikult võrdeline selle pinna pindalaga. Summeerides sellised pinnad vahemikus $n=0\rightarrow\infty$, saame nn.positiivse faasi võimsuse.

Täpselt samal moel, lähtudes punktidest, mille korral $s=(2n+1){\lambda\over 2}$, leiame negatiivse faasi võimsuse. Nende vahe ongi kiirguse intensiivsus antud punktis.

 
Huygens'i-Fresnel'i printsiip. Mida teha vahepealsete punktidega, kus lainefrondi kaugus vaatluspunktist on 0 ja $\pi$ vahepealne? Et ka need kiirgavad lainet, tuleb seegi arvesse võtta. Muidugi liituvad need lained vastavalt amplituutide reeglile, st. faasinihet arvestades. Nii tekib uus front kõigi vana frondi poolt kiiratud lainete summana.

See ongi Fresnel'i täiendus Huygens'i printsiibile. Kokku saame:

1. Iga lainefrondi punkti võime vaadata kui sekundaarlainete allikat;

2. Uus lainefront tekib sekundaarlainete interferentsi tulemusel.

Huygens-Fresneli printsiipi võib vaadelda kui Young'i katse üldistust.Kui Youngil tekkis interferentspilt kahe ava (või pilu) poolt lainefrondist eraldatud piirkondadest tulevate lainete interferentsil, siis nüüd "mängib kaasa" kogu front.

Järelikult on igasugused takistused laine levikul kirjeldatavad matemaatiliste piirangutena interferentsi valemis. Käes on jälle üks "üldine eeskiri", mille poole füüsikud kogu aeg püüdlevad.

Huygens'i-Fresnel'i printsiip seob uue lainefrondi kujunemise sekundaarlainete interferentsiga.

NB! Huygens'i-Fresnel'i printsiip töötab mõlemas suunas:

interfereeruvad ka põhilainele vastassuunda levivad sekundaarlained.

Kuidas selle järgi arvutada? Alustame lihtsuse mõttes tasalainest ja vaatleme lõpmatu tasandi kujulise lainefrondi mingi riba poolt punktis $B$ tekitatud võnkumist. Reaalsuses vastaks see küllalt suurele (lainepikkusega võrreldes!) avale laine teel.

Punkt $B$ asub tasandist $LF$ (lainefront) kaugusel $l=vt$, kus $v$ on laine levimiskiirus. Iga frondi lõik laiusega $\Delta x$ tekitab punktis $B$ võnkumise, mille amplituud ja faas sõltuvad riba kaugusest. Et tegu on silinderlainega, väheneb amplituud pöördvõrdelisena kaugusega $s=\sqrt{l^2+x^2}$:

$$A=A_0{{S_x}\over s}=A_0{{\Delta x\times{\rm laius}}\over\sqrt{l^2+x^2}}.$$

Faasinihe punktidest $x$ ja $x=0$ tulevate lainete vahel on:

$$\varphi=2\pi{{(s-l)}\over\lambda}=2\pi{{\sqrt{x^2+l^2}-l}\over\lambda}$$

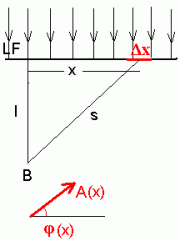
Lainefrondi lõik $\Delta x$ ja tema poolt punktis B tekitatava sekundaarlaine faasidiagramm (phasor).

Näeme, et osalaine amplituud kahaneb, hilinemine faasis aga kasvab eemaldumidel punktist $x=0$ $\pm\infty$ poole.

Summeerimine faasi arvestades polegi nii lihtne töö, integreerimine seda enam.

Amplituudide reegel $A^2=AA_1^2+A_2^2+2A_1A_2\cos\varphi$ ei võimalda kuidagi tavalist, nn kumulatiivset summeerimist, kus uus liidetav lihtsalt lisatakse eelmiste summale. Siin tuleb kõigepealt võtta ruutjuur, seejärel leida uus faasinurk, lahutada see järgmise liidetava faasist (et leida faasinihet järgmise liitmistehte tarbeks), ning alles siis saab liitmist jätkata. Integreerimine muutub aga sootuks võimatuks.

Tuleb hakkama saada vektoritega. Neid me küll integreerida ei oska, aga summeerida saab isegi kahte viisi. Kolme vektorit saame liita näiteks rakendades rööpkülikureeglit või viies järgmise liidetava alguse eelmise lõppu

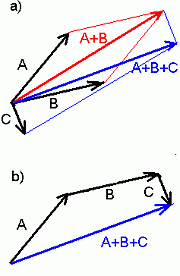
Vektorite liitmine: a) rakendades rööpkülikureeglit;
b) viies järgmise liidetava alguse eelmise lõppu

Tuleme tagasi oma interferentsipildi juurde. Iga $x$ väärtusele vastab vektor amplituudiga $A_i$ ja faasinurgaga $\varphi_i$. $x$ kasvades esimene neist kahaneb, lähenedes nullile, teine aga kasvab piiramatult.

 

Liites selliseid vektoreid, saame omapärase spiraalse kõvera, mida nimetatakse Cornu' spiraaliks.

Meie poolt otsitavaks summaks on vektor koordinaatide $\xi,\eta$ alguspunktist (vastab punktile $x=0$) "viimase" vektori lõpp-punkti. $x$ lähenedes lõpmatusele keerdub spiraal punktiks koordinaatidega $\xi_P,\eta_P$, mida nimetatakse spiraali pooluseks.

Spiraali saab jätkata ka $x$ negatiivsete väärtuste suunas; kui lugeda seal $A$ negatiivseks saame spiraalile teise, punkti (0,0) suhtes sümmeetrilise haru, mis samuti lõpeb poolusega.

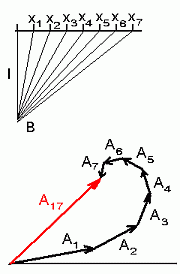
Siin on liidetud seitsmelt lainefrondi lõigult tulevate sekundaarlainete faasivektorid.

Näeme, et takistamata tasalaine amplituud võrdub pooluste vahelise kaugusega $\xi\eta$-tasandil.

Kui kasutada nüüd mehaanikast tuntud koordinaatmeetodit (vektorite summaks on vektor, mille koordinaadid on võrdsed liidetavate vektorite vastavate koordinaatide summaga), saame anda Cornu spiraali parameetrilisel kujul:

$$\xi=\sum{A\Delta x_i\cos\varphi}=\int\limits _{x_1}^{x_2}A_0\... ...(2\pi{{\sqrt{x^2+l^2}-l}\over\lambda}){{dx}\over\sqrt{x^2+l^2}}$$

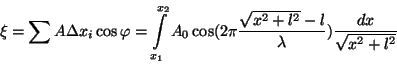
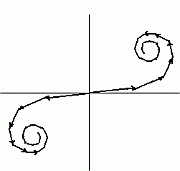
Faasivektorite summa üle lainefrondi lõigu, mis vastab käiguvahele -1.5 kuni +1.5 lainepikkust.

$$\eta=\sum{A\Delta x_i\sin\varphi}=\int\limits _{x_1}^{x_2}A_0... ...(2\pi{{\sqrt{x^2+l^2}-l}\over\lambda}){{dx}\over\sqrt{x^2+l^2}}$$

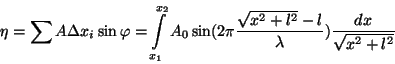
Integreerimispiirkonnaks on siin lainefrondi suvaline osa vahemikus $-\infty<x_1,x_2<\infty$.

Ega needki integraalid lihtsad ei ole - analüütiline lahend puudub. Matemaatiliste teisenduste abil saab neid aga taandada hästiuuritud spetsiaalfunktsioonidele - nn. Fresnel'i integraalidele. Arvuti jaoks pole nad loomulikult mingi probleem.

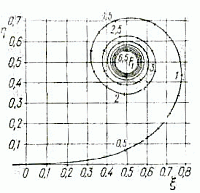
Lõpmatu lainefrondi faasikõver - Cornu' spiraal.

Vaatame nüüd graafiliselt, kuidas Fresnel'i meetod võimaldab arvutada difraktsioonipilti sirge servaga tõkke taga.

Pooltasandile langev tasalaine ja punktid 1 - 8, kus mõõdetakse valguse intensiivsust. Servast lõpmata kaugetele punktidele vastavad poolused P1 ja P2.	Mõõtepunktide asukohad Cornu' spiraalil.	Heledusjaotus ekraani serva taga. Valguse intensiivsuse igas mõõtepunktis määrab summaarse laine amplituud, selle omakorda faasivektor - vastava punkti kaugus poolusest P1. Terava serva asemel näeme heledate ja tumedete triipude vaheldumist.

Langegu tasalaine tõkkele risti; $x$-telje võtame tõkke tasandis, risti selle servaga. Valime tõkke taga rea punkte $P_1,~P_2,~\dots,~P_5$. Asugu punkt $P_3$ geomeetrilise varju piiril.

Joonistame Cornu' spiraali ja võtame sellelt punktidele $P_1~\dots~P_5$ vastavad amplituudid $A_1~\dots~A_5$. Arvestades, et laine (valguse!) intensiivsus on võrdeline amplituudi ruuduga, joonestame heleduse käigu varju piiril: Et tegelik heleduskäik on just selline, seda on katsetes korduvalt kontrollitud.

Nüüd, teades täpset lahendit, võime tuletada ka ligikaudse.

Selleks lõikame Cornu spiraali poolust läbiva sirgege pooleks. Joonest allapoole jäävad nüüd meie "plusstsoonid"; nende laius on võrdeline joone alla (peale) jääva spiraali lõigu pikkusega ning neile vastav liidetav amplituudi avaldises - lõikejoone pikkusega spiraali sama keeru kahe lõikepunkti vahel.

Selleks, et lainefront tsoonideks jagada, pole vaja isegi spiraali. Kuna lõikepunktid vastavad $\varphi$ väärtustele ${\pi\over 2}$, ${{3\pi}\over 2}$, tuleb tsoonipiirid tõmmata kaugustele, kus $s-l=(2n+1){\lambda\over 4}$. Jääb üle veel jagada tsooni laius $s$-ga ning tulemused liita.

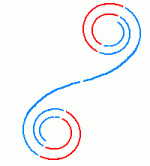
Fresnel'i tsoonid Cornu' spiraalil. Sinised paaris-tsoonid suurendavad valguse intensiivsust, punased (paaritud) aga vähendavad. Maksimaalse intensiivsuse saame paarituid tsoone kinni kattes.

 

Fraunhoferi difraktsioon. Kõige efektsemalt töötab tsoonide meetod kitsa pilu taga tekkiva kiirgusvälja korral. Pilu taga tekkivat lainet võib sel juhul vaadelda silinderlainena; et difraktsiooniribad on kitsad, võime piisavalt suurel kaugusel silinderpinna kõverust ühe riba piirkonnas mitte arvestada. Saame intensiivsuse sõltuvuse nurgast, mille vaadeldav suund moodustab pilule langeva valguse suunaga.

Esimesel joonisel näidatud suunas (nurk $\alpha$) on pilu tagumisest servast tuleva kiire poolt läbitud tee $l\sin\alpha$ võrra pikem esimesest servast tuleva kiire omaga võrreldes.
Olgu see antud näites $2\lambda$.

Pilu jaguneb nüüd neljaks võrdse laiusega tsooniks, millelt tulevate lainete summaarsed amplituudid on võrdsed. Et kaks neist on pluss-, kaks aga miinustsoonid, tuleb kiirguse summaarne amplituud null ning pilu paistab sellest suunast vaadates tumedana.

Teisel joonisel (nurk $\beta$) "mahub pilusse" kolm tsooni - seetõttu on summaarne amplituud nullist erinev ja pilu paistab heledana.

Seega on pilu läbinud kiirguse maksimumide tingimus ($l$ - pilu laius):

$$l\sin\alpha=n\lambda$$

 

Difraktsioonivõre. Mis saab aga siis, kui kõik paaristsoonid mustaks värvida?

Siis polegi muud, kui et liituvad paaritud tsoonid, ja kõik samas faasis. Kiirgus võimendub ulatudes (teoreetiliselt) pooleni tsentraalmaksimumi intensiivsusest

Aga see pole ainuke efekt. Kui ühe pilu korral on maksimumid lamedad (üleminek miinimumile toimub sujuvalt, sedavõrd kui "avaneb" järgmine tsoon), siis mitme pilu korral, eriti kui pilude arv on suur, tähendab tühine nurga muutus kaugemate võrepilude minekut vastasfaasi.

Parimaid tulemusi annab Fresnel'i teooria difraktsiooni arvutamisel

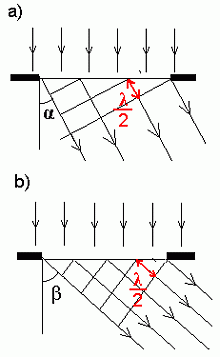
Fraunhofer'i difraktsioon pilult.

1. pilusse mahub 3 tsooni - pilu paistab heledana
2. pilusse mahub 4 tsooni - pilu paistab tumedana.

Kui mingile vaatenurgale vastavad tsoonid "üle ühe" läbipaistmatuks muuta, saame difraktsioonivõre, mida saab kasutada lainepikkuste eristamiseks maksimumile vastava vaatenurga järgi.

Sellise, sadadest ja tuhandetest piludest koosneva difraktsioonivõre taga koosneb laineväli kitsastest kiirtest, mida eraldavad ulatuslikud peaaegu täiesti "pimedad" vahemikud. Maksimumide valem vastab kahetsoonilisele pilule:

$$\sin\alpha=\pm{{k\lambda}\over d},$$

kus $d$ on nn. võrekonstant - kaugus kahe naaberpilu keskpunktide vahel. Täisarv $k$ tähistab maksimumi järku.

Maksimumidele vastava nurga sõltuvus lainepikkusest võimaldab kasutada difraktsioonivõret spektraalriistana. Tema abil saab lihtsalt ja täpselt mõõta valguse lainepikkust.

 
Keralaine difraktsioon. Veidi teistsuguse metoodikaga saab arvutada difraktsiooni tsentraalsümmeetriliste tõkete taga.

Vaatame näiteks valguskiire teele jäävat ümmargust auku, mida valgustab punktallikas. Auguni jõudnud lainefront kujutab endast kerapinda, mille raadius võrdub augu serva kaugusega allikast.

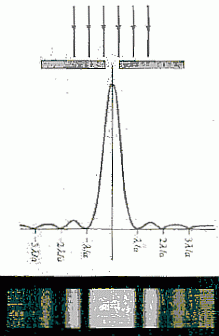
Intensiivsuste jaotus pilu taha pandud ekraanil.

Et leida valguse intensiivsust punktis, mis asub augu taga allika ja augu tsentriga ühel sirgel, tuleks eelneva põhjal jagada augule vastav lainefrondi osa tsoonideks. Teeme seda, lähtudes frondi kaugusele vaatluspunktist: esimese tsooni piiriks on käiguvahe $\lambda/4$; teisel, esimesega vastasfaasis oleval tsoonil $3\lambda/4$ jne. Tsoonide raadiused ja pindalad arvutame, lähtudes geomeetrilistest kaalutlustest.

Nagu pilugi korral, sõltub ka siin valguse intensiivsus tsoonide arvust ja pindaladest. Et vähemalt telje lähedal on Fresnel'i tsoonid enam-vähem võrdsete pindaladega (tõestage!), tähendab paarisarv tsoone valgustamata, paaritu arv aga valgustatud punkti. Et kindla raadiusega augu korral sõltub tsoonide arv vaatluspunkti (ekraani) kaugusest, võib augu "varju" keskkoht olla nii hele kui tume.

Teljest eemaldumine tähendab ava nihutamist pildil, kus tsoonid on juba välja joonistatud. Proovige seda teha graafiliselt, joonistades paberile tsoonid, värvides paaritud mustaks ja nihutades saadud pildil teist paberilehte, millesse on lõigatud umbes kolme tsooni suurune ava. Püüdke hinnata musta ja valge pinna vahekorda - te näete, et see sõltub ava asendist. Kuna pilt on sümmeetriline, tähendab viimane, et ekraanile tekib heledate ja tumedate kontsentriliste rõngaste süsteem.

Mis juhtub, kui tõkkeks on ketas? Arutleme järgnevalt: kui tõket ei ole, tuleb kohale kogu valgus. Tõke varjab sellest osa, mis võib olla null, kui varjatud tsoone on paarisarv. Sel juhul peaks varju keskel olema hele täpp. Kui varjatud on paaritu arv tsoone, tuleb kaotsiläinud valgus nullist erinev - keskpunkt peaks olema tumedam. Mõlemale järgnevad vahelduvad kontsentrilised rõngad.

Saveljevi õpikus (I. Saveljev. Füüsika, 3. kd., lk. 88) tuuakse arutlus, mille järgi on varju tsentris alati hele täpp. Kumba loogikat uskuda?

Suurte avade või tõkete korral see muidugi ei kehti. Siis on parem rakendada pooltasandi kohta käivat teooriat.

 
Tsooniplaat ja Fresnel'i läätsed. Nagu Fraunhoferi difraktsiooni korral, võime ka nüüd paaris (või paaritud) tsoonid mustaks värvida. Efekt on aga palju vägevam kui difraktsioonivõre korral. Nimelt

võimendab iga must rõngas mõõtepunktini tulevat valgust, kusjuures võimendustegur võrdub rõngaste arvuga. See nn. tsooniplaadi fantastiline omadus saab veel fantastilisemaks, kui oleme sellise riistapuu valmis teinud ja vaatame läbi selle.

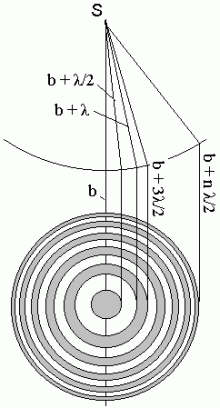
Keralaine difraktsioon. Kui paaritud Fresnel'i tsoonid kinni katta, tekib nn. tsooniplaat, mis toimib (suurendava) läätsena.

Meie käes on lääts, mis suurendab tema taha jäävaid esemeid.

Kuidas selline lääts töötab, milline on tema fookusekaugus ja kuidas tekib kujutis, jäägu teile välja mõelda. Kirjandust võite kasutada.

 

Mikroskoobi ja teleskoobi piirlahutusvõime. Ülaltoodust võib jääda mulje, et difraktsioon on üks kasulik nähtus. Seda kindlasti, kuid optiliste riistade suurendusele paneb just tema piiri.

Geomeetrilisest optikast mäletame, et optilised riistad sisaldasid läätsi või peegleid. Nende läbimõõt püütakse teha võimalikult suur (et suurendada valgusjõudu), aga tehnilised võimalused on ikkagi piiratud. Seetõttu kujutab iga lääts või diafragma tõket valguslaine levikul, ning see toob kaasa difraktsiooni.

Valguse difraktsioon paneb piiri optiliste riistade nurklahutusvõimele.

Kui läätse asemel oleks lihtsalt ava, oskaksime difraktsioonipilti arvutada. Pilt koosneb rõngastest millede raadiused vastavad ava raadiusele vastava Fresnel'i tsooni laiusele. Et tsoonide laius ava suurenedes kahaneb, tähendab ava suurenemine rõngaste läbimõõtude vähenemist difraktsioonipildis ($r_m\sim\sqrt m$,   seega   $\Delta r=r_{m+1}-r_m\sim\sqrt{m+1}-\sqrt m$).

Rõngaste täpsete läbimõõtude leidmine on tõsine matemaatikaülesanne - selleks tuleb arvutada interferentsipilt ekraani tasandis.

Ligikaudse arvutuse skeem on järgmine:
vaatame objektiivile (avale) langevas tasalaines kujunevaid Fresnel'i tsoone ning loeme esimese miinimumi asukoha kauguse tsentrist (tsentraalmaksimumist) ligikaudu võrdseks viimase avasse mahtuva tsoomi laiusega $\Delta r~$.

Lugedes ava "väikeseks" (st., väike on avasse mahtuvate tsoonide arv), saame mõningate matemaatiliste manipulatsioonide tulemusel

$$\Delta r={{b\lambda}\over{2r}},~~{\rm millest}~~\varphi ={{\Delta r}\over b}={\lambda\over{2r}}={\lambda\over D}.$$

Täpne arvutus üle Besseli funktsioonide annab tulemuseks $\sin\varphi =1.22{\lambda\over D}.$ See ongi pikksilma nurklahutusvõime.

Mikroskoobi jaoks tuleb meil lahendada pöördülesanne: leida ava taga asuva punkti poolt objektiivi läbimisel tekkiva (tasa?)laine intensiivsuse sõltuvus vaatenurga muutusest. Joonistan skeemi ja väidan, et vastus tuleb poole väiksem teleskoobi omast. Tõestage!

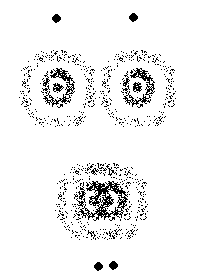
Kahe lähestikuse punkti kujutised geomeetrilise ja laineoptika järgi.
Alumisel pildil on difraktsioonirõngad ühte sulanud, kuigi geomeetrilise optika järgi peaksid punktid eraldi näha olema. (1818)

 

Difraktsioon ruumilistelt tõketelt. Kujutame ette, et valguskiire teel on mitte ainult üks tõke (või ava) vaid terve tõkete süsteem. Meie valemite abil saab rehkendada näiteks ühe võre läbinud laine käitumist teise, esimesega nurga alla paikneva võre läbimisel. Iga interferentsiriba (hele joon ekraanil) jaguneb nüüd omakorda ribadeks" - tekib korrapäraselt paiknevate valguslaikude süsteem, kusjuures laikude omavahelised kaugused sõltuvad võrekonstantidest ja valguse lainepikkusest.

Et kristallis paiknevad aatomid korrapäraselt, kihtidena, tekib siinkohal idee uurida kristalli ehitust, kasutades selleks valguskiirte difraktsiooni kristallvõres. Paraku on aatomitevahelised kaugused (suurusjärk 10 nm) oluliselt väiksemad valguse lainepikkusest. Küll aga on võimalik sel otstarbel kasutada röntgenikiiri.

Esialgu matemaatiliselt võimatuna tundunud probleemile leidus vapustavalt geniaalne lahendus:

Kujutleme, et vaatame kristalli "servalt". Et aatomid paiknevad korrapäraselt, on teatud nurkade all vaadates näha "kiht" - kõik aatomid paistavad olevat ühes tasandis. Sõltuvalt kristalli omadustest on selliseid nurki, mille all kristall kihtide vahelt läbi paistab, üsna palju. Juba lihtsaima kuubilise võre korral saab joonistada hulga tasandeid. Kujutame nüüd, et tasalaine langeb sellisele kihile mingi nurga all. Kui teha oletus, et laine peegeldub aatomkihilt, saame maksimumide tingimuseks

$$2d\sin\theta=\pm m\lambda.$$

See on eksperimentaalfüüsikas hästituntud Wulff-Bragg'i valem.

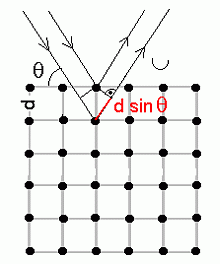
Bragg'i valem - "peegeldumine aatomtasanditelt"

Seose avastas 23-aastane Adealide'i ülikooli tudeng William Lawrence Bragg oma isa, professor William Henry Bragg'i laboris 1913.a.

Füüsikaliselt on valem täielik jama (kristallis pole mingeid peegeldavaid tasandeid!), aga ta töötab (miks, selle kohta pakuvad oma selgitusi nii füüsikaline optika kui kvantmehaanika) niivõrd efektiivselt, et isa-poeg Bragg'id said juba 1915.a. nii Nobeli preemia (absoluutne kiirusrekord!) kui ka aadlitiitli.

Ka tänapäeval on röntgenstruktuuranalüüs põhiline meetod aine ehituse uurimisel.

Röntgenstruktuuranalüüs, mille abil on avastatud näiteks pärilikkuseaine DNA struktuur, põhineb ruumilistel tõketel hajuva kiirguse interferentsil

 

Hologramm (vaata ka lisateksti). Laineoptika kõige fantastilisem rakendus on siiski holograafia (kr. holos = tervik + grapho = kujutan). Idee jäädvustada valgustundliku keskkonna abil interferentsil tekkiv ruumiline seisevlaine tekkis inglise füüsikul D. Gabor'il juba 1947.a., aga enam-vähem talutava realisatsioonini jõuti alles 30 aasta pärast.

Holograafiline pildistamine seisneb valgusallika kiirguse jagamises kaheks koherentseks kiirtekimbuks, milledest esimene valgustab pildistatavat eset ja pärast sellelt hajumist interfereerub teise, nn. tugikimbuga.

Piirkonda, kus kiirtekimbud lõikuvad ja tekib interferentspilt, paigutatakse valgustundlik materjal (fotoemulsioon). Viimases toimuvad keemilised protsessid, mille tulemusena keskkond muutub ebaühtlaseks - valgust saanud kohtades tekkiv hõbedapuru hajutab pärast ilmutamist temale langevat valgust tugevamini, kui ülejäänud emulsioon.

Kui sellist "fotot" (nn. hologrammi) valgustada analoogse valgusallikaga, tekib hajunud kiirte interferentsi tulemusel pildistatava lainega identne kiirtekimp, mida inimene tajub kui pildistatavalt esemelt tulevat valgust.

Laineoptika tarberakenduseks on täisruumiliste fotode valmistamine - holograafia.

Korralik hologramm jätab vapustava mulje: kindlas suunas vaadates näeme õhus rippuvat "kangastust", mille tõepärasus lausa sunnib "käega katsuma". Midagi pihku ei jää, käsi läheb viirastusest vabalt läbi, selle tõelisust muutmata.

Hologrammi võib vaadata eri suundadest, uurida luubiga, uuesti pildistada - ta on niisama tõeline kui oli pildistatav ese.

Kahjuks on edu holograafia alal raske tulema ja seetõttu häid hologramme vähe. Asi tahab veel õppimist.

SISUKORDA
ALGUSESSE