Loeng 15. Lisatekst
Euleri valem
Võnkumiste ja lainetega seotud matemaatiliste probleemide
lahendamisel kasutame sageli seost
mida matemaatikud tunnevad Euleri võrrandite nime all. Mitmus
on selle pärast, et tavaliselt käivad need võrrandid paarikaupa,
teine on
Võrranditel on hea omadus: nad lubavad kasutada paljudes valemites
trigonomeetriliste funktsioonide asemel eksponentfunktsiooni. Seda
aga on võrratult lihtsam korrutada ja jagada, integreerimisest
rääkimata. Vajadusel saab kergesti tagasi trigonomeeetriliste
funktsioonide juurde minna - kui selline vajadus üldse tekib.
Elektriinsenerid teevad suure osa oma rehkendustest nagunii
kompleksarvudes.
Euleri valemid põhinevad astmeridade teoorial. Kinemaatika osas,
liikumisvõrrandi tuletamisel, rääkisime otsitava valemi arendamisest
nn. Maclaurini ritta:
Teeme seda nüüd kolme funktsiooniga:
kuna
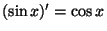
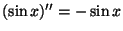
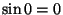 ja
ja 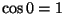 .
.
Analoogiliselt saame
Ja nüüd arendame ritta imaginaarse astendajaga eksponendi:
Rühmitamisel on eksponentfunktsioonile vastavas reas eraldatud reaal-
ja imaginaarosad. Kui võrrelda seda trigonomeetriliste funktsioonide
ritta-arendustega, näeme, et (vaatamata ridade lõpmatusele, aga miks?) on
See ongi Euleri valem. Kõik ülejäänu on sellest tuletatav.